Der Satz des Pythagoras
Werbung

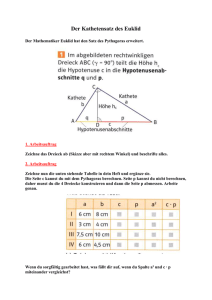
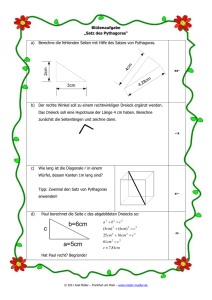
Einer der berühmtesten Sätze Der Welt. Pythagoras von Samos * 570 v. Chr. +510 v. Chr. Geburt auf der Insel Samos Antiker griechischer Philosoph Lehre bei Thales und Anaximandros den Genies der damaligen Zeit. Das Rechtwinklige Dreieck a und b sind die beiden Katheten. Sie schließen den 90° -Winkel ein. Die Hypotenuse ist c. Sie liegt dem 90° Winkel gegenüber. Die Lehre des Satzes von Pythagoras Formel: a²+b²=c² Die Lehre des Satzes von Pythagoras Formel: c²-b²=a² Beispielaufgabe: geg.: b=5cm,c=12cm ges.: a=? a2 + b2 = c2 a2 + (5cm)2 = (12cm)2 a2 +25cm2 = 144cm2 a2= 119cm2 a = 10.9cm Die Lehre des Satzes von Pythagoras Formel: a²-c²=b² Beispielaufgabe: geg.: c=10cm , a=2cm ges.: b=? a2 + b2 = c2 (2cm)2 + b2 = (10cm)2 4cm2 + b2 = 100cm2 b2 = 96cm2 b = 9.8cm Höhensatz des Euklid Formel h²=p*q Beispielaufgabe geg.:p*q ges.: h Lsg.:h² = p*g h = p*q geg.: ges.: Lösung.: h Die Formel zur Erinnerung: H²=p*q Kathetensatz des Euklid Formeln b² = q · c Bzw. Beispiel auf der nächsten Seite a² = p · c Beispielaufgabe Bei der Konstruktion eines Gestells sind die Längen c und p bekannt. Die Längen a und b müssen nun noch bestimmt werden. Gegeben: c = 5cm ; p = 2cm Gesucht: a; b Lösung: q=c-p q = 5cm - 2cm q = 3cm a2 = c · p a2 = 5cm · 2cm a2 = 10cm2 / Wurzel ziehen a = 3,16cm b2 = c · q b2 = 5cm · 3cm b2 = 15cm2 / Wurzel ziehen b = 3,87cm Die Formeln zur Erinnerung: b²=q*c / a²=p*c Jetzt weißt du das Grundlegende von Pythagoras Auf diesen Seiten findest du weitere Aufgaben zum Pythagoras http://www.frustfrei-lernen.de/mathematik/satz-des-pythagorasaufgaben-uebungen-mathematik-loesungen.html http://www.klassenarbeiten.net/klassenarbeiten/uebungen/klasse9/math ematik/pythagoras_dreieckberechn.shtml http://www.poenitz-net.de/Mathematik/2.Geometrie/2.8.A.Pythagoras.pdf