Vortest "Winkel, Parallelogramme und Dreiecke"

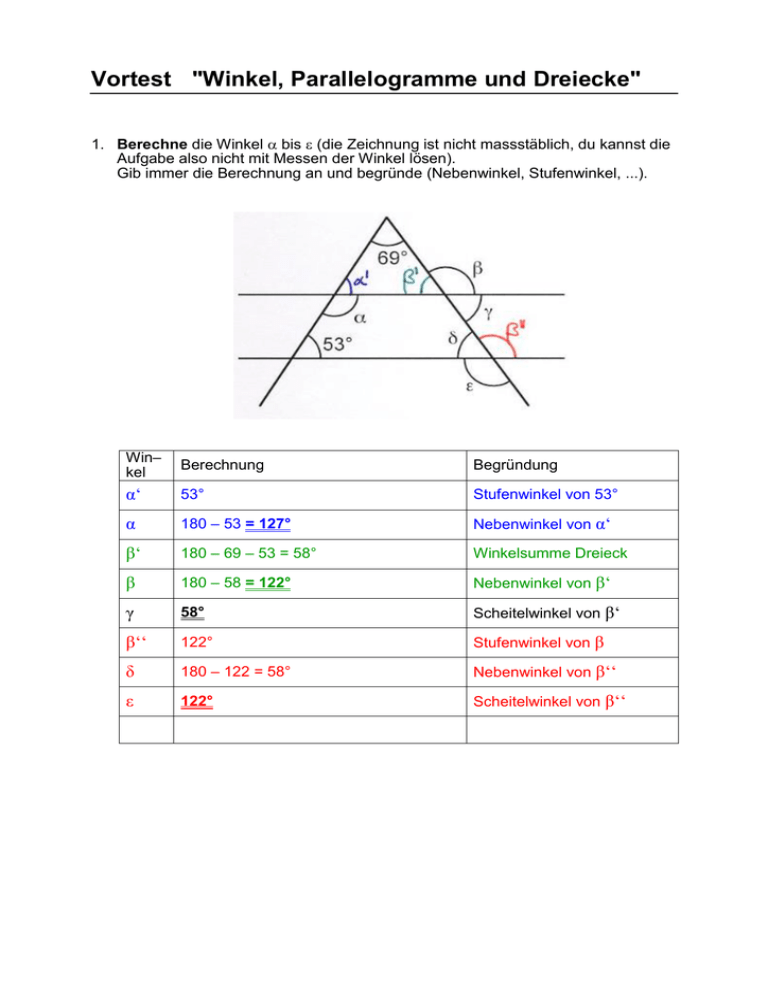
Vortest "Winkel, Parallelogramme und Dreiecke"
1. Berechne die Winkel  bis  (die Zeichnung ist nicht massstäblich, du kannst die
Aufgabe also nicht mit Messen der Winkel lösen).
Gib immer die Berechnung an und begründe (Nebenwinkel, Stufenwinkel, ...).
Win–
kel
Berechnung
Begründung
α‘
53°
Stufenwinkel von 53°
α
180 – 53 = 127°
Nebenwinkel von α‘
β‘
180 – 69 – 53 = 58°
Winkelsumme Dreieck
β
180 – 58 = 122°
Nebenwinkel von β‘
γ
58°
Scheitelwinkel von β‘
β‘‘
122°
Stufenwinkel von β
δ
180 – 122 = 58°
Nebenwinkel von β‘‘
ε
122°
Scheitelwinkel von β‘‘
2. Berechne die Fläche A und die Höhe hc.
a = 4cm, b = 3cm, c = 5cm
A=
ab 43
=
= 6cm2
2
2
hc  c
=A
2
hc  5
=6
2
hc ∙ 5 = 12
hc = 12 : 5 = 2,4cm
3. Konstruiere folgende Figuren:
a) Rechteck: a = 6cm, b = 3cm



Seite a zeichnen, 6cm lang, das
gibt A und B
senkrecht zu a bei A 3cm
abtragen, das gibt D
senkrecht zu a bei B 3cm
abtragen, das gibt C
∙
∙
A
B
b) Parallelogramm: a = 6cm, b = 4cm, ha = 3cm



Seite a zeichnen, das
gibt A und B
eine Parallele zu a im
Abstand ha = 3cm
zeichnen
Kreis um A und B mit
Radius 4cm, das gibt
C und D
4cm
D
C
ha
∙
A
B
c) Dreieck: a= 5cm, ha = 4cm, b = 7cm



Seite a zeichnen, gibt B und C
eine Parallele zu a im Abstand ha = 4cm
zeichnen
Kreis um B mit Radius 7cm, das gibt A
1. Lösung
2. Lösung
7cm
1,7m
4. Die vertikalen Wände eines abgeschrägten Zimmers sollen
tapeziert werden. Die nicht zu
tapezierende Fläche der Türe
misst 1,1m x 2,1m. Berechne die
Fläche, die tapeziert werden muss.
C
A
2,4m
1,7
1,6
B
C
3,3m
0,7
2,4
1,7
3,3
C: A□ - A∆ = (3,3 ∙ 2,4) – (
1,6  0,7
) = 7,92 – 0,56 = 7,36m2
2
A: 4 ∙ 2,4 – 1,1 ∙ 2,1 = 9,6 – 2,31 = 7,29m2
B: 4 ∙ 1,7 = 6,8m2
Total: A + B + 2C = 7,29m2 + 6,8m2 + 2 ∙ 7,36m2 = 28,81m2
4m
1,7m
5. Für die gezeichneten Parallelogramme gelten die Masse:
I
a = 12m
II
r = 5,5m
h = 2,8m
s = 12m
III
p = 1800cm
q = 24m
IV
m = 12m
h = 9,9m
Beantworte zu jeder Figur die folgenden Fragen:
a) Wie heissen die einzelnen Figuren?
b) Berechne für jede Figur den Umfang in m.
c) Ermittle für jede Figur die Fläche.
I
Quadrat
u = 4 ∙ 12m = 48m
A = 12 ∙ 12 = 144m2
II
Parallelogramm
u = 2 ∙ 5,5 + 2 ∙ 12 = 35m
A = 12 ∙ 2,8 = 33,6m2
III Rechteck
u = 2 ∙ 18 + 2 ∙ 24 = 84m
A = 18 ∙ 24 = 432m2
IV Rhombus
u = 4 ∙ 12 = 48m
A = 12 ∙ 9,9 = 118,8m2