Übungen zur Trigonometrie

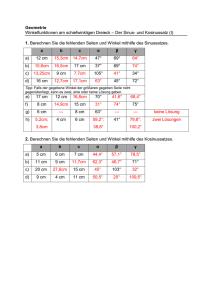
Bernd Sumpf
Eichberg1 • 07987 Reudnitz 03661/435814 • [email protected]
Übungen zur Trigonometrie
1.
Bestimmen Sie jeweils alle fehlenden Stücke des Dreiecks!
a)
b)
C
C
9,5 cm
B
c
7,6
m
A
A
c)
d)
A
e)
7cm
72
°
58°
7cm
C
C
32°
B
A
7cm
41°
B
f)
C
67
°
A
B
7cm
3cm
5cm
C
A
2.
B
29°
24°
6,4cm
B
Die Höhe eines Turms kann ermittelt werden, auch wenn man nicht an seinen Fußpunkt herankommt. Bestimmen Sie die Höhe h aus den Angaben in der Skizze!
(erst , dann , dann BC, dann h)
C

h
A
64m
B
°
53
Bestimmen Sie den Umfang des Vierecks und die Größe des Winkels ∢ADC !
D
7°
10
52
°
3.

24°
A
C
32°
64m
B
Bernd Sumpf
Eichberg1 • 07987 Reudnitz 03661/435814 • [email protected]
Lösungen:
1a)
1b)
1c)
1d)
1e)
1f)
Pythagoras: AC=5,7cm; cos =7,6/9,5 =36,87°; Innenwinkelsumme: =53,13°
Innenwinkelsumme: =61°; cos(29°)=7/(BC) BC=8,00cm; Pythagoras: AC=3,87cm
Innenwinkel: =90°; sin(32°)=(BC)/7 BC=3,71cm; sin(58°)=(AC)/7 AC=5,94cm
Innenwinkel: =67°;Sinussatz: AC=4,99cm und BC=7,23cm
Kosinussatz: BC=6,83cm; Sinussatz: =42,37° ( nicht eindeutig, siehe 1f) ; Innenw.:=70,63°
Sinussatz: sin =0,8677 ergibt zwei Winkel !!! 1=60,19° und 2=119,81°
mit 1: Innenwinkel:=95,81° ; Sinussatz: AC=7,34cm
mit 2: Innenwinkel:=36,19° ; Sinussatz: AC=4,36cm
C
A
3cm
C
24°
6,4cm
B
A
24°
6,4cm
3c
m
B
2)
=127° =29° BC=53,69m h=42,88m
Der Turm ist etwa 43 Meter hoch.
3)
∢ACB=58° ∢ACD=49° ∢ADC=79°
im Dreieck ABC:
tan(32°)=BC/64m BC=39,99m; cos(32°)=64m/AC (oder Pythagoras) im Dreieck ACD:
Sinussatz: CD=60,58m und AD=58,02m
AC=75,47m; Umfang des Vierecks u = AB + BC + CD +AD
u = 222,59m (sinnvoll runden auf 222,6m oder 223m)