Die kosmischen oder astronautischen Geschwindigkeiten

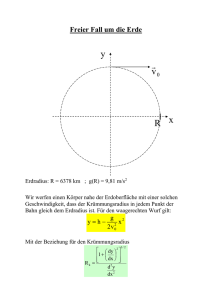
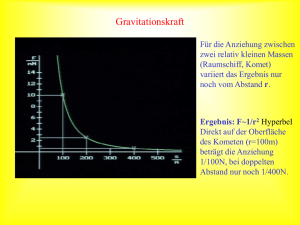
Die kosmischen oder astronautischen Geschwindigkeiten
Die Grenzgeschwindigkeit oder erste kosmische Geschwindigkeit.
Definition:
Unter der Grenzgeschwindigkeit oder der ersten kosmischen Geschwindigkeit
(Formelzeichen: vG) versteht man diejenige Geschwindigkeit, die ein von der Oberfläche
eines Zentralkörpers (Erde, Mond usw.) senkrecht zur Oberfläche nach oben
geschossener Probekörper bei einer Vernachlässigung der Reibungskräfte haben muss,
um bis zu einer Höhe des einfachen Radius des Zentralkörpers aufzusteigen.
Berechnung der Grenzgeschwindigkeit:
( )
1 1
r1 r2
W = γ • m • m0
Wenn man den Radius des Zentralkörpers mit r bezeichnet, so ist
r1 = r und r2 = 2r
zu setzen.
Für die Arbeit ergibt sich dann:
W = γ • m • m0
(
1 1
r 2r
)
=γ•
m • m0
2r
Diese Grenzenergie muss gleich der kinetischen Energie sein, mit der der Körper
senkrecht zur Erdoberfläche nach oben geschossen wird. Es gilt also:
mm0
1
m0 v 2G = γ
2
2r
Daraus ergibt sich für die Grenzgeschwindigkeit:
vG = γ
m
r
Die Grenzgeschwindigkeit ist von der Masse des nach oben geschossenen Körpers
unabhängig. Sie ist eine für jeden Himmelskörper charakteristische Konstante.
Die Grenzgeschwindigkeit tritt auch noch bei einer anderen Satellitenbewegung auf. Ein
Probekörper mit der Masse m0 soll einen kugelförmigen Zentralkörper (Erde, Mond usw.)
mit der Masse m in gleichbleibendem Abstand umkreisen, wobei dieser Abstand klein
gegenüber dem Radius r des Zentralkörpers ist. Damit eine solche Kreisbahn zustande
kommt, muss die Radialkraft in jedem Bahnpunkt gleich der Gravitationskraft sein. Als
Bahnradius kann der Radius r des Zentralkörpers betrachtet werden. Dann ergibt sich die
Gleichung:
m0 v 2
mm 0
=γ 2
r
r
24
Oder
vG = γ
m
r
Dies bedeutet:
Wenn man einen Satelliten von einem wenig über der Oberfläche eines Zentralkörpers
gelegenen Punkt in waagerechter Richtung mit der Grenzgeschwindigkeit VG abschießt,
so beschreibt er in kleinem, gleichbleibenden Abstand eine Kreisbahn um den
Zentralkörper. Dabei darf natürlich keine Reibung vorhanden sein.
Aufgabe: Bestimmen Sie die Grenzgeschwindigkeit für die Erde und den Mond.
[Ergebnis: vG,E=7,9km/s; vG,M=1,68km/s]
http://www.schulphysik.de/java/physlet/applets/grav7.html
http://www.schulphysik.de/java/physlet/applets/newtonberg.html
Die Fluchtgeschwindigkeit oder die zweite kosmische Geschwindigkeit.
Definition:
Unter der Fluchtgeschwindigkeit oder der zweiten kosmischen Geschwindigkeit
(Formelzeichen: vF) versteht man diejenige Geschwindigkeit, die ein von der Oberfläche
eines Zentralkörpers (Erde, Mond usw.) senkrecht zur Oberfläche nach oben
geschossener Probekörper bei einer Vernachlässigung der Reibungskräfte mindestens
haben muss, um aus dem Gravitationsfeld des Zentralkörpers entfliehen zu können.
Die Fluchtgeschwindigkeit kann mit der oben bereits verwendeten Formel
W = γ • m • m0
( )
1 1
r1 r2
berechnet werden.
Wenn man den Radius des Zentralkörpers mit r bezeichnet, so ist
r1 = r und r =
1
=0
r2
zu setzen.
Die Arbeit, die aufgewendet werden muss beträgt:
WF = γ •
m • m0
r
25
Diese Fluchtenergie muss dem Probekörper also beim Abschluss in Form von kinetischer
Energie mitgegeben werden. Daher ist
mm 0
1
m0 v F2 = γ
2
r
Aus dieser Formel folgt:
vF = γ
2m
r
vF = 2 • v G
Die Fluchtgeschwindigkeit ist von der Masse des vertikal nach oben geschossenen
Körpers unabhängig. Sie ist eine für jeden Himmelskörper charakteristische Konstante.
Aufgabe: Bestimmen Sie die Fluchtgeschwindigkeit für die Erde und den Mond.
[Ergebnis: vF,E=11,2km/s; vF,M=2,36km/s]
Die Fluchtgeschwindigkeit hat für die Satellitenbewegung noch eine weitere Bedeutung.
Es wurde bereits darauf hingewiesen, dass die Arbeit, die erforderlich ist, um einen
Probekörper in einem Gravitationsfeld von einem Punkte P1 zu einem Punkte P2 zu
bewegen, unabhängig von dem dabei durchlaufenen Wege ist. Dies gilt natürlich auch für
den hier behandelten Fall. Die zur Entfernung des Probekörpers aus dem Gravitationsfeld
erforderliche Fluchtenergie ist unabhängig von dem Wege auf dem das Entweichen aus
dem Gravitationsfeld erfolgt. Dies bedeutet:
Um einen Flugkörper von der Oberfläche eines Zentralkörpers (Erde, Mond usw.) aus
dessen Gravitationsfeld zu entfernen, kann er unter einem beliebigen Winkel mit
mindestens der Fluchtgeschwindigkeit abgeschossen werden.
Die dritte kosmische Geschwindigkeit.
Es gilt die folgende Definition:
Unter der dritten kosmischen Geschwindigkeit oder der dritten astronautischen
Geschwindigkeit (Formelzeichen: vF,So ) versteht man diejenige Geschwindigkeit, mit der
ein Flugkörper von der Erde in ihrer Bewegungsrichtung abgeschossen werden muss, um
aus dem Gravitationsfeld der Sonne zu entweichen.
Zur Berechnung der dritten kosmischen Geschwindigkeit gehen wir wieder von der Formel
W = γ • m • m0
( )
1 1
r1 r2
aus.
In diese Gleichung ist die Sonnenmasse m =1,99. 1030 kg und der Radius der
näherungsweise als Kreis betrachteten Erdbahn r1 = 1,5. 1011 m einzusetzen; ferner gilt
1
wieder r = = 0 . Damit ergibt sich:
r2
v1 = γ
26
2m
r1
Aufgabe: Bestimmen Sie die Geschwindigkeit damit ein Satellit von der Erde aus das
Gravitationsfeld der Sonne verlassen kann.
[Ergebnis: v1,E=42km/s]
Ein von der Erde in Richtung der Erdumlaufsbewegung abgeschossener Flugkörper
verlässt das Gravitationsfeld der Sonne, wenn die Abschussgeschwindigkeit relativ zur
Erde mindestens gleich
vF,So=16,6km/s.
ist.
Die vierte kosmische Geschwindigkeit.
Definition:
Unter der vierten kosmischen Geschwindigkeit oder der vierten astronautischen
Geschwindigkeit (Formelzeichen: vF,Mi) versteht man diejenige Geschwindigkeit, mit der
ein Flugkörper von der Erde in der günstigsten Richtung abgeschossen werden muss,
damit er aus dem Milchstraßensystem entweicht.
Wenn hier von der günstigsten Richtung gesprochen wird, so ist damit gemeint, dass die
Umlaufsgeschwindigkeit der Sonne um das Zentrum des Milchstraßensystem ausgenutzt
wird, ähnlich wie dies beim Verlassen des Sonnensystems mit der
Umlaufsgeschwindigkeit der Erde um die Sonne geschehen ist. Eine hier nicht
durchgeführte Rechnung zeigt:
Die vierte kosmische Geschwindigkeit beträgt
vF,Mi = 100 km/s.
27