Öffnen

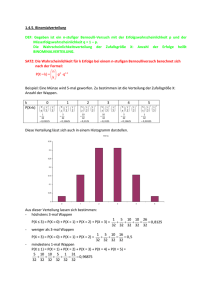
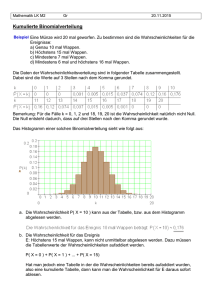
VI Stochastik
Erarbeitung
Was erwarten Sie?
Vorüberlegungen
1 Bei einem Glücksspiel werden drei ideale Münzen gleichzeitig geworfen. Der Einsatz beträgt 5 €. Liegen
alle drei Münzen mit dem Wappen nach oben, erhält man 20 € ausbezahlt. Bei allen anderen Spielausgängen
beträgt die Auszahlung pro oben liegendem Wappen 2 €.
Führen Sie die folgenden Schritte durch, um beurteilen zu können, ob es sich auf lange Sicht hin gesehen
lohnt, dieses Spiel zu spielen.
a) Bestimmen Sie den Gewinn (d. h. Auszahlung minus Einsatz), den man bei einem Spiel mit 0, 1, 2 bzw. 3
Wappen erzielt, sowie die Wahrscheinlichkeiten, mit denen die jeweiligen Spielausgänge auftreten. Tragen
Sie die Ergebnisse in die Tabelle ein. Beachten Sie: Verluste werden als negative Gewinne angegeben.
Anzahl Wappen
0
1
2
3
Gewinn
Wahrscheinlichkeit
b) Stellen Sie sich nun vor, dass Sie dieses Spiel sehr oft spielen (z. B. 800-mal) und füllen Sie den folgenden
Lückentext aus: Bei 800 Spielen kann man erwarten, dass …
… bei
Spielen 0 Wappen oben liegen. Bei jedem dieser Spiele beträgt der Gewinn
€.
… bei
Spielen 1 Wappen oben liegt. Bei jedem dieser Spiele beträgt der Gewinn
… bei
Spielen 2 Wappen oben liegen. Bei jedem dieser Spiele beträgt der Gewinn
€.
… bei
Spielen 3 Wappen oben liegen. Bei jedem dieser Spiele beträgt der Gewinn
€.
€.
Berechnen Sie nun den gesamten Gewinn, den Sie bei 800 Spielen erwarten können. Berechnen Sie dann
daraus den durchschnittlich pro Spiel zu erwartenden Gewinn.
2 Das nebenstehende Glücksrad, bei dem alle Sektoren gleich wahrscheinlich sind,
wird ein Mal gedreht. Der Einsatz beträgt 5 €, ausgezahlt wird die erdrehte Zahl in €.
a) Berechnen Sie den Gewinn, den eine Spielerin bzw. ein Spieler durchschnittlich
pro Spiel erwarten kann. Gehen Sie dabei vor wie in Aufgabe 1.
b) Mareike behauptet: „Den durchschnittlich zu erwartenden Gewinn pro Spiel
erhalte ich ebenso, wenn ich jeden möglichen Gewinn mit der zugehörigen
Wahrscheinlichkeit multipliziere und die Summe dieser Produkte bilde.“ Überprüfen
Sie diese Aussage.
Zahl
0
4
7
25
Gewinn (in €)
Wahrscheinlichkeit
Bei z. B. 1200 Spielen erwartet man, dass …
… bei
Spielen die Zahl 0 erscheint. Bei jedem dieser Spiele beträgt der Gewinn
€.
… bei
Spielen die Zahl 4 erscheint. Bei jedem dieser Spiele beträgt der Gewinn
€.
… bei
Spielen die Zahl 7 erscheint. Bei jedem dieser Spiele beträgt der Gewinn
€.
… bei
Spielen die Zahl 25 erscheint. Bei jedem dieser Spiele beträgt der Gewinn
© Ernst Klett Verlag GmbH, Stuttgart 2015 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
€.
Was erwarten Sie? − Lösungen
1 a)
Anzahl Wappen
Gewinn (in €)
Wahrscheinlichkeit
0
1
2
3
−5
−3
−1
15
1
8
3
8
3
8
1
8
b) Bei 800 Spielen kann man erwarten, dass …
… bei 100 Spielen 0 Wappen oben liegen. Bei jedem dieser Spiele beträgt der Gewinn − 5 €.
… bei 300 Spielen 1 Wappen oben liegt. Bei jedem dieser Spiele beträgt der Gewinn − 3 €.
… bei 300 Spielen 2 Wappen oben liegen. Bei jedem dieser Spiele beträgt der Gewinn − 1 €.
… bei 100 Spielen 3 Wappen oben liegen. Bei jedem dieser Spiele beträgt der Gewinn 15 €.
Gesamter erwarteter Gewinn bei 800 Spielen:
100  (− 5 €) + 300  (− 3 €) + 300  (− 1 €) + 100  15 € = − 200 €.
Pro Spiel zu erwartender Gewinn = − 200 € : 800 = − 0,25 €. Pro Spiel erwartet man 25 Cent Verlust.
2 a)
Zahl
0
4
7
25
Gewinn (in €)
−5
−1
2
20
Wahrscheinlichkeit
5
12
2
12
4
12
1
12
Bei z. B. 1200 Spielen erwartet man, dass …
… bei 500 Spielen die Zahl 0 erscheint. Bei jedem dieser Spiele beträgt der Gewinn − 5 €.
… bei 200 Spielen die Zahl 4 erscheint. Bei jedem dieser Spiele beträgt der Gewinn − 1 €.
… bei 400 Spielen die Zahl 7 erscheint. Bei jedem dieser Spiele beträgt der Gewinn 2 €.
… bei 100 Spielen die Zahl 25 erscheint. Bei jedem dieser Spiele beträgt der Gewinn 20 €.
Gesamter erwarteter Gewinn bei 1200 Spielen:
500  (− 5 €) + 200  (− 1 €) + 400  2 € + 100  20 € = 100 €.
Pro Spiel zu erwartender Gewinn = 100 € : 1200 =
1
12
€. Pro Spiel erwartet man
1
12
€ Gewinn.
b) Mit der Formel von Mareike erhält man den
Erwartungswert E = (− 5 €)  5 + (− 1 €)  2 + 2 €  4 + 20 €  1 = 1 €.
12
12
12
12
12
Maike hat recht, sie erhält den gleichen Wert wie in Aufgabenteil a). Es kann gezeigt werden, dass diese
Formel allgemein gültig ist, da sich die Anzahl der Spiele bei der Berechnung in Aufgabenteil a) herauskürzen
lässt.
© Ernst Klett Verlag GmbH, Stuttgart 2015 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.