EK2_2014_12_05_Loesung

Elektronik 2
Name:
Kurztest 2: 5.12.14
Klasse:
Musterlösung
Dauer:
30 Minuten
Hilfsmittel:
Eigene Notizen, Taschenrechner,
sowie Skripte „RealerOperationsverstaerker.pdf“ und „filter_active_v5.pdf“
Punkte:
Jede vollständig richtig gelöste Teilaufgabe gibt 3 Punkte,
falls der Lösungsweg klar ersichtlich ist.
Tipps:
Zuerst alle Aufgaben durchlesen und mit der einfachsten beginnen
Teilaufgaben unabhängig lösbar (Ausnahmen sind angegeben)
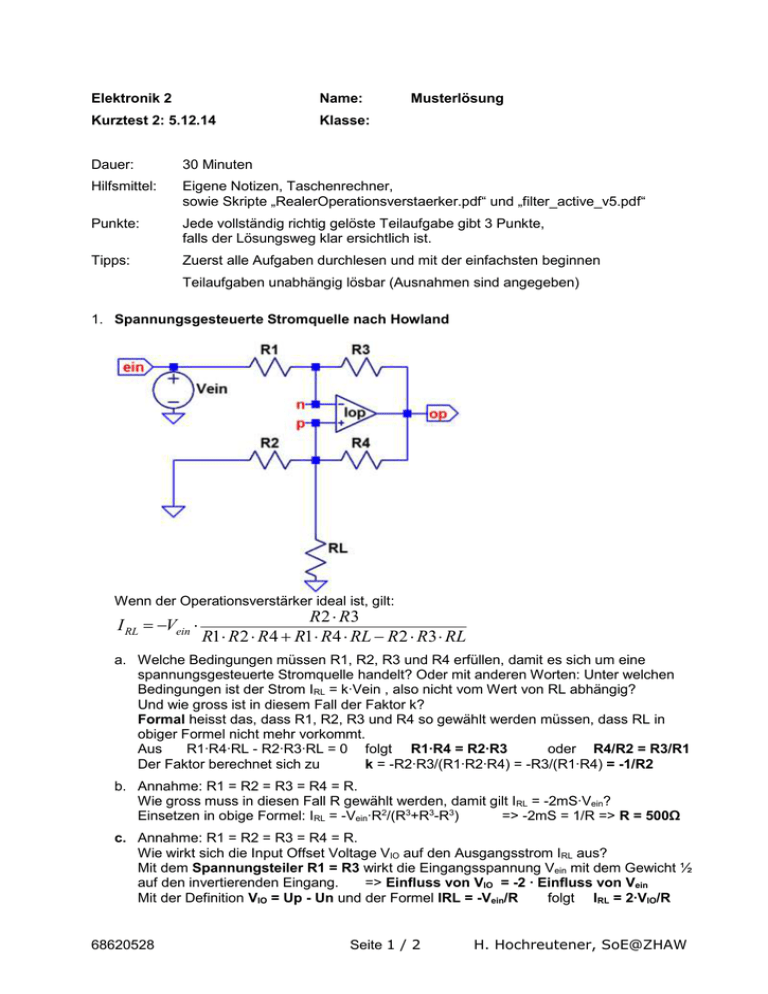
1. Spannungsgesteuerte Stromquelle nach Howland
Wenn der Operationsverstärker ideal ist, gilt:
I RL  Vein 
R 2  R3
R1 R2  R4  R1 R4  RL  R2  R3  RL
a. Welche Bedingungen müssen R1, R2, R3 und R4 erfüllen, damit es sich um eine
spannungsgesteuerte Stromquelle handelt? Oder mit anderen Worten: Unter welchen
Bedingungen ist der Strom IRL = k∙Vein , also nicht vom Wert von RL abhängig?
Und wie gross ist in diesem Fall der Faktor k?
Formal heisst das, dass R1, R2, R3 und R4 so gewählt werden müssen, dass RL in
obiger Formel nicht mehr vorkommt.
Aus
R1∙R4∙RL - R2∙R3∙RL = 0 folgt R1∙R4 = R2∙R3
oder R4/R2 = R3/R1
Der Faktor berechnet sich zu
k = -R2∙R3/(R1∙R2∙R4) = -R3/(R1∙R4) = -1/R2
b. Annahme: R1 = R2 = R3 = R4 = R.
Wie gross muss in diesen Fall R gewählt werden, damit gilt IRL = -2mS∙Vein?
Einsetzen in obige Formel: IRL = -Vein∙R2/(R3+R3-R3)
=> -2mS = 1/R => R = 500Ω
c. Annahme: R1 = R2 = R3 = R4 = R.
Wie wirkt sich die Input Offset Voltage VIO auf den Ausgangsstrom IRL aus?
Mit dem Spannungsteiler R1 = R3 wirkt die Eingangsspannung Vein mit dem Gewicht ½
auf den invertierenden Eingang.
=> Einfluss von VIO = -2 ∙ Einfluss von Vein
Mit der Definition VIO = Up - Un und der Formel IRL = -Vein/R
folgt IRL = 2∙VIO/R
68620528
Seite 1 / 2
H. Hochreutener, SoE@ZHAW
2. Anti-Aliasing-Filter
3dB-Tschebbycheff-Filter, Grenzfreq. fg = 4kHz, Verstärkung |Ua/Ue| = 20, Ua < 2Vpp
a.
Dimensionieren sie die Widerstände und Kondensatoren.
Lösung mit Formeln aus dem Skript und Taschenrechner.
Hier wird die Matlab-Lösung mit Kommentaren gezeigt:
clc; clear; format compact; format short eng;
A0 = -20;
fg = 4000;
a1 = 1.0650; b1 = 1.9305;
% Verstärkung
% Grenzfrequenz
% aus Tabelle für gewünschten Filtertyp
C1 = input('C1 wählen: ');
% Provisorische Wahl
C2 = C1;
C2_C1 = 4*b1*(1-A0)/(a1^2);
% Formel 2.6.30
while (C2 < C1*C2_C1)
C2 = input(['C2 wählen, wobei C2 > ' num2str(C1 * C2_C1) ' : ']);
Kondensator wählen
end
% Formlen 2.6.29
R2 = ( a1*C2 -sqrt(a1^2*C2^2 -4*C1*C2*b1*(1-A0)) ) / (4*pi*fg*C1*C2)
R1 = R2/(-A0)
R3 = b1 / ( 4*pi^2*fg^2*C1*C2*R2 )
% 2.
disp('Falls die Widerstandswerte zu tief/hoch => alle C und R proportional anpassen.');
Und das ist die Ausgabe des Skripts:
C1 wählen: 1e-9
C2 wählen, wobei C2 > 1.4297e-07 : 150e-9
R2 =
16.6012e+003
R1 =
830.0607e+000
R3 =
1.2273e+003
Falls die Widerstandswerte zu tief/hoch => alle C und R proportional anpassen.
In der Regel unproblematisch sind Widerstandswerte zwischen 1kΩ und 100kΩ.
b. Es ist vorgesehen einen OpAmp mit SR = 0.5V/µs und GBP = 1MHz einzusetzen.
Reichen diese Daten für obiges Filter?
SRbenötigt = 2∙π∙fg∙Up = 2∙π∙fg∙Ua/2 = 0.025V/µs
=> ausreichend
GBPbenötigt = fg∙|A0| = 80kHz
=> ausreichend
OpAmp kann eingesetzt werden.
68620528
Seite 2 / 2
H. Hochreutener, SoE@ZHAW