PHYSIK GRUNDWISSEN 8

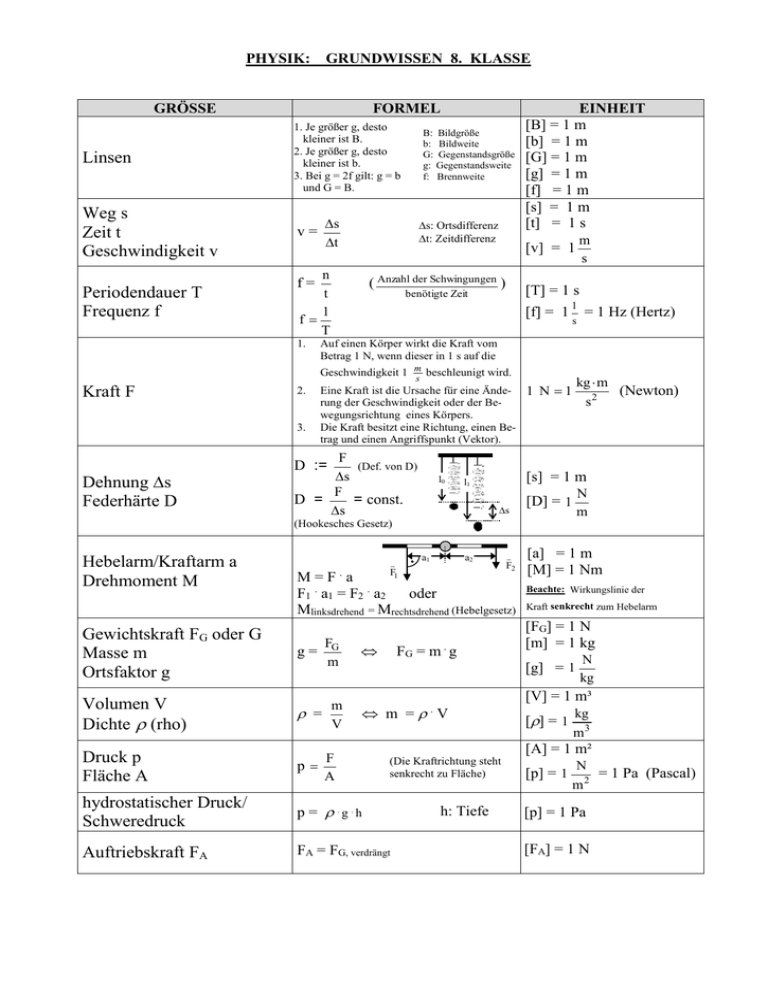
PHYSIK:
GRUNDWISSEN 8. KLASSE
GRÖSSE
FORMEL
Linsen
1. Je größer g, desto
kleiner ist B.
2. Je größer g, desto
kleiner ist b.
3. Bei g = 2f gilt: g = b
und G = B.
Weg s
Zeit t
Geschwindigkeit v
v=
Periodendauer T
Frequenz f
s
t
s: Ortsdifferenz
t: Zeitdifferenz
n
t
1
f
T
[T] = 1 s
[f] = 1 1 = 1 Hz (Hertz)
benötigte Zeit
s
Auf einen Körper wirkt die Kraft vom
Betrag 1 N, wenn dieser in 1 s auf die
Geschwindigkeit 1 m beschleunigt wird.
s
Kraft F
2.
3.
Dehnung s
Federhärte D
Eine Kraft ist die Ursache für eine Änderung der Geschwindigkeit oder der Bewegungsrichtung eines Körpers.
Die Kraft besitzt eine Richtung, einen Betrag und einen Angriffspunkt (Vektor).
F
(Def. von D)
s
F
D =
= const.
s
D :=
l0
s
a1
a2

F2
M=F.a
F1 . a1 = F2 . a2
oder
Mlinksdrehend = Mrechtsdrehend (Hebelgesetz)
g=
Volumen V
Dichte  (rho)
m
 =
V
Druck p
Fläche A
F
p
A
hydrostatischer Druck/
Schweredruck
p =  .g .h
Auftriebskraft FA
FA = FG, verdrängt
FG
m

N
m
[D] = 1
D

F1
Gewichtskraft FG oder G
Masse m
Ortsfaktor g
kg  m
(Newton)
s2
1 N 1
[s] = 1 m
l1
(Hookesches Gesetz)
Hebelarm/Kraftarm a
Drehmoment M
m
s
[v] = 1
( Anzahl der Schwingungen )
f=
1.
B: Bildgröße
b: Bildweite
G: Gegenstandsgröße
g: Gegenstandsweite
f: Brennweite
EINHEIT
[B] = 1 m
[b] = 1 m
[G] = 1 m
[g] = 1 m
[f] = 1 m
[s] = 1 m
[t] = 1 s
FG = m . g
[a] = 1 m
[M] = 1 Nm
Beachte: Wirkungslinie der
Kraft senkrecht zum Hebelarm
[FG] = 1 N
[m] = 1 kg
[g] = 1
 m = V
.
N
kg
[V] = 1 m³
[] = 1
kg
m3
[A] = 1 m²
(Die Kraftrichtung steht
senkrecht zu Fläche)
h: Tiefe
[p] = 1
N
= 1 Pa (Pascal)
m2
[p] = 1 Pa
[FA] = 1 N
Musteraufgaben
1. Zur Dichte: Ein Gefäß, das leer die Masse m1  0,50 kg hat, wird zunächst mit Wasser gefüllt.
Die Masse des mit Wasser gefüllten Gefäßes beträgt dann 20,5 kg. Jetzt werden noch Bleikugeln der Masse m 2  3,0 kg in das Wasser geschüttet. Das Volumen des Gemisches Wasser und
Blei beträgt 20,31 l. ( Wasser  998
kg
m3
).
Berechne die Dichte der Bleikugeln!
Lösung:
m
20 kg
mWasser  20 ,5 kg  0,50 kg  20 kg; VWasser  Wasser 
 20 ,04 l ;
Wasser 998 kg
m3
mBleikugel
3,0 kg
g
VBleikugel  20 ,31 l  20 ,04 l  0,27 l ;  Bleikugel 

 11
;
3
VBleikugel
0,27 dm
cm3
2. Zur Geschwindigkeit: Die erste Hälfte einer 48 km langen Strecke legt ein Radfahrer mit der
Geschwindigkeit 30 km/h zurück, die zweite Hälfte mit der Geschwindigkeit 24 km/h. Berechne die Durchschnittsgeschwindigkeit für die Gesamtstrecke!
Lösung:
s1
24 km
s
24 km

 0 ,80 h ,  t 2  2 
 1,0 h ;
km
km
v1
v
2
30
24
h
h
s ges
48 km
2 km
km
t ges  t1  t 2  1,8 h ;
v 

 26
 27
;
t ges
1,8 h
3 h
h
t 1 
3. Zu Kraft, Gewicht und Masse: Eine elastische Schraubenfeder ist 18,0 cm lang. Hängt man
eine Waagschale, auf der ein Apfel liegt, an die Feder, so dehnt sie sich auf eine Länge von
23,0 cm. Waagschale und Apfel haben zusammen das Gewicht 2,50 N. Nimmt man den Apfel
von der Waagschale weg, so zieht sich die Feder um 4,00 cm zusammen. Berechne die Federhärte D sowie das Gewicht und die Masse des Apfels!
Lösung:
s1  23 ,0 cm  18 ,0 cm  5 ,0 cm; D 
G Apfel  D  s2  0 ,500
F1
2 ,50 N
N

 0 ,500
;
s1
5,0 cm
cm
N
 4 ,00 cm  2 ,00 N ;
cm
m Apfel 
G Apfel
g

2 ,00 N
 204 g
N
9 ,81
kg
4. Zum Hebelgesetz: Ein Mann mit dem Gewicht 800 N läuft auf einem Brett der Länge 10 m,
das auf den Punkten A und B aufliegt und das Gewicht 500 N hat. Wie weit darf er über A
hinaus nach links gehen, ohne dass das Brett kippt?
A
AB  6,6 m
Lösung:
Wähle als Drehpunkt den Punkt A ! Der Schwerpunkt des Bretts liegt 1,6 m rechts von A.
500 N 1,6 m
FBrett  1,6 m  FMann  x ; x 
 1,0 m
800 N
Er darf also 1,0 m weit über A hinaus nach links gehen.
B