Vorwort
Werbung
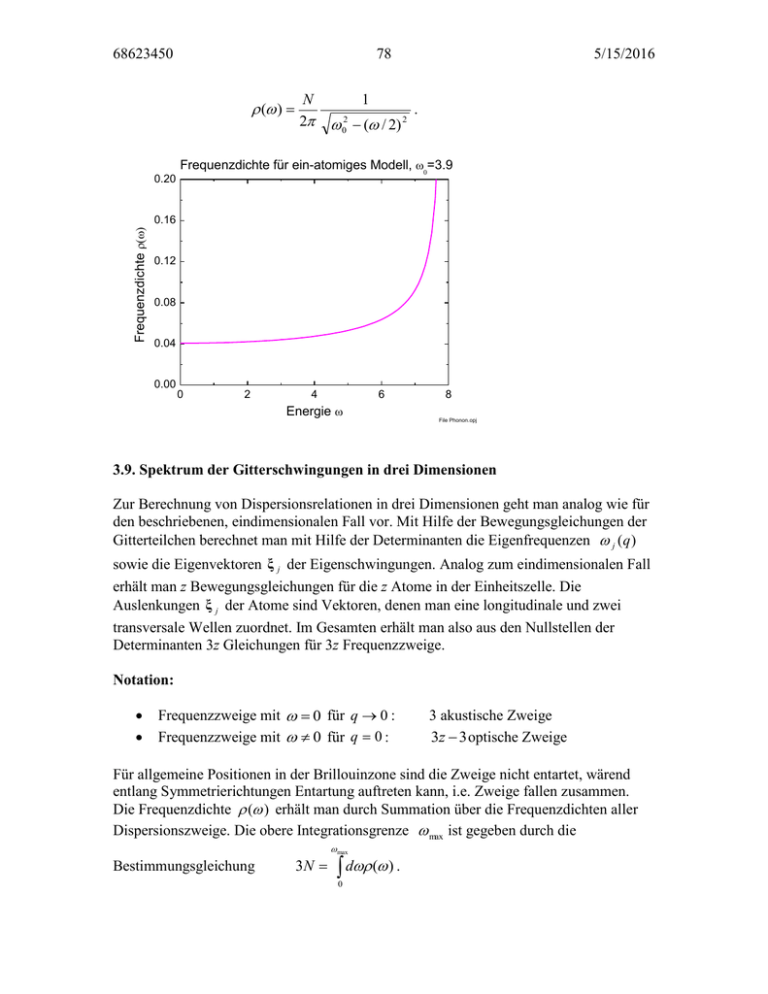
68623450 78 ( ) 0.20 N 2 1 02 ( / 2) 2 5/15/2016 . Frequenzdichte für ein-atomiges Modell, =3.9 Frequenzdichte 0.16 0.12 0.08 0.04 0.00 0 2 4 6 Energie 8 File Phonon.opj 3.9. Spektrum der Gitterschwingungen in drei Dimensionen Zur Berechnung von Dispersionsrelationen in drei Dimensionen geht man analog wie für den beschriebenen, eindimensionalen Fall vor. Mit Hilfe der Bewegungsgleichungen der Gitterteilchen berechnet man mit Hilfe der Determinanten die Eigenfrequenzen j (q ) sowie die Eigenvektoren ξ j der Eigenschwingungen. Analog zum eindimensionalen Fall erhält man z Bewegungsgleichungen für die z Atome in der Einheitszelle. Die Auslenkungen ξ j der Atome sind Vektoren, denen man eine longitudinale und zwei transversale Wellen zuordnet. Im Gesamten erhält man also aus den Nullstellen der Determinanten 3z Gleichungen für 3z Frequenzzweige. Notation: Frequenzzweige mit 0 für q 0 : Frequenzzweige mit 0 für q 0 : 3 akustische Zweige 3z 3 optische Zweige Für allgemeine Positionen in der Brillouinzone sind die Zweige nicht entartet, wärend entlang Symmetrierichtungen Entartung auftreten kann, i.e. Zweige fallen zusammen. Die Frequenzdichte ( ) erhält man durch Summation über die Frequenzdichten aller Dispersionszweige. Die obere Integrationsgrenze max ist gegeben durch die Bestimmungsgleichung 3N max d ( ) . 0 68623450 79 5/15/2016 Überall, wo die Ableitung der Dispersionsrelation nach dem Wellenvektor ein Maximum erreicht, wird ( ) maximal sein. Beachte, dass (0) 0 ist für Kristalle mit mehr als zwei räumlichen Dimensionen. Analog wie für das Debye- oder das Einsteinmodell ordnet man jeder Eigenschwingung einen harmonischen Oszillator zu der aufgrund der Quantenmechanik quantisiert ist. Der Beitrag der Gitterschwingungen zur inneren Energie ist gegeben durch U s (V , T ) max ( ) 1 2 n d mit 0 n 1 exp( /( k B T )) 1 und die spezifischen Wärme ist gegeben durch CV (T ) U s (V , T ) . T In den folgenden zwei Figuren zeigen wir die Dispersionsrelationen von Kupfer und die daraus resultierende Frequenzdichte (E. C. Svensson, B. N. Brockhouse and J. M. Rowe, Phys. Rev. 155, 619 (1967)). Kupfer kristallisiert in der kubisch flächenzentrierten Form, hat also 4 Atome pro kubischer Zelle. Da die primitive Zelle aber nur ein Atom enthält ist z 3 und man beobachtet nur akustische Zweige. Entlang der [1 0 0] und der [1 1 1] Richtung sind die zwei transversalen Moden entartet und man beobachtet nur einen transversalen und einen akustischen Zweig. Beachte: Die Frequenz /( 2 ) ist in Einheiten 11012 s-1 = 1THz ausgedrückt. Dispersionsrelationen entlang den Hauptsymmetrierichtungen in Kupfer (Svensson et al., Phys. Rev. 155, 619 (1967)). 68623450 80 5/15/2016 Aus der Kenntnis der Dispersionskurven aller Zweige, kann die Frequenzdichte ( ) berechnet werden und damit die spezifische Wärme CV (T ) / T U s (T ,V ) . 1. Brillouinzone mit einigen eingezeichneten, wichtigen Punkten hoher Symmetrie. Aus den obigen Dispersionsrelationen berechnete Frequenzdichte ( ) . Beachte: 2 (Svensson et al., Phys. Rev. 155, 619 (1967). 3.10. Impuls von Phononen, Kristallimpuls Wie bereits erwähnt besteht zwischen der Quantisierung von elektromagnetischen Schwingungen in einem quaderförmigen, verspiegelten Hohlraum und den Gitterschwingungen in einem Medium ein enger Zusammenhang. Für elektromagnetische Wellen definiert man Photonen durch die Angabe des Wellenvektors k und der (zwei möglichen) Polarisationsrichtungen s. Die Anzahl der Photonen der Sorte k, s ist dann gegeben durch die Verteilung nk , s (exp( s /( k B T ))) 1 . Die Energie der Photonen kann sich aufgrund der 68623450 81 5/15/2016 quantenmechanischen Behandlung als harmonischer Oszillator nur in ganzen Quanten s (k ) ändern. Photonen sind Bose Teilchen mit Spin 1. Analog kann man den Gitterschwingungen Schallquanten zuordnen, die man als Phononen bezeichnet. Man ordnet ihnen eine Energie j (q) einen Impuls K q G k und einen Spin 0 zu. ( 2 / q ) Hier bezeichnet j den Dispersionszweig und q denWellenvektor des Phonons in Bezug auf die 1. Brillouinzone. Den Vektor K bezeichnet man als Kristallimpuls. Die Zahl nq , j (exp( j /( k B T ))) 1 gibt an, wieviele Phononen mit der Energie j (q) bei der Temperatur T angeregt sind. Während sich das Photon mit der Lichtgeschwindigkeit c ausbreitet, bewegt sich das Phonon mit der Schallgeschwindigkeit c s . Obwohl bei der Ausbreitung einer Gitterschwingung im zweitlichen Mittel, wie beim Photon, keine Materie transportiert wird (Ausnahme: LA-Phonon bei q 0 ), ordnet man dem Photon formal den Kristallimpuls K zu. Der Begriff des Impulses erlaubt eine einfache Beschreibung von Streuproblemen mit Phononen. Beispiele für Streuprozesse: Photon – Phonon: Lichtstreuung (Brillouin- oder Ramanstreuung), Streuung von Röntgen- oder Synchrotronstrahlung (Braggreflexion, inelastisch) ki kf ki q kf Phonon – Phonon: z. B. Wärmeleitung q 68623450 82 5/15/2016 q2 q q1 Phonon – Neutron: Messung von Dispersionsrelationen Phonon – Magnon: magnetoelastische Effekte etc. Für Streuprozesse gelten die Gesetze für Impuls- und Energieerhaltung: Impulserhaltung: k f k i K k i (q G k ) Energieerhaltung: s , f s ,i j . Notation: k f , k i : Wellenvektoren des gestreuten (final) und einfallenden (incident) Photons K q G k : Kristallimpuls K, reduzierter Wellenvektor q, reziproker Gittervektor Gk s , f , s ,i : Energie des Photons nach und vor dem Streuprozess j : Phononenenergie. Beachte, dass die Phononenenergie aufgrund der Periodizität des Gitters nur von q abhängt. 3.11. Rückstossfreie Emission von Photonen: Mössbauer Effekt Die geometrischen Bedingungen zur Beobachtung von Braggpeaks wurden hergeleitet unter der Annahme eines streng periodischen Gitters. Wir haben gesehen, dass Braggreflexion nur möglich ist, wenn der Wellenvektor des einfallenden Photons einen Gitterpunkt mit dem Rand einer Brillouinzone verbindet. Die Impulserhaltung lautet aufgrund der Ewald’schen Konstruktion k f k i (q G k ) k i G k , gleichbedeutend mit k i k f Q . 68623450 83 5/15/2016 Bei der Reflexion des Photons wird auf den Kristall der Masse M der Impuls Q (k i k f ) übertragen. Als Beispiel betrachten wir die Rückstossenergie auf einen 1 g schweren Kristall mit Kupfer K -Strahlung (8.8 keV): ER 2 Q 2 2 (2k i ) 2 2 2 (k i c) 2 2( ) 2 . 2M 2M Mc 2 Mc 2 Beachte: Qmax 2k i . Damit erhalten wir E R 2 2 8800 eV 1.6 10 19 Cb 10 29 Mc 2 10 -3 g (3 10 8 ms ) 2 Der Streuprozess kann also als wirklich elastisch betrachtet werden, solange der Kristallimpuls vom Kristall als ganzes übernommen wird und nicht von den einzelnen Atomen. Die Energie der Photonen ändert sich bei Braggreflexion praktisch nicht. Es werden keine Gitterschwingungen erzeugt, da offensichtlich q 0 und j 0 ist. Dies nennt man einen Nullphononen-Prozess. Die inelastische Streuung kann ebenfalls als Stossprozess aufgefasst werden. Man unterscheidet Einphononen-Prozesse: es wird ein Phonon erzeugt k f k i q G k Mehrphononen-Prozesse: obwohl weniger wahrscheinlich, können mehrere Phononen gleichzeitig erzeugt und/oder vernichtet werden: k f k i qi G k . i Durch die Wirkung der Phononen werden die Photonen in verschiedene Richtungen gestreut. Dies führt zu einem “diffusen” Untergrund von Streuung zwischen den Braggpeaks und insbesondere auch bei den Braggpositionen selbst. Beide Effekte führen zu einer Erniedrigung der Braggpeaks. Die Abnahme der Braggintensität in Funktion der Temperatur ist gegeben durch den Debye-Waller Faktor. Er ist ein Mass für das Auftreten von Nullphononen-Prozessen und nimmt mit zunehmender Temperatur ab. 68623450 84 5/15/2016 Der Mössbauer Effekt (1958, TUM) ist eine direkte Konsequenz des Auftretens von Nullphononen-Prozessen in Kristallen. Ein freier, ruhender Atomkern geht von einem angeregten Zustand Ea unter Emission eines -Quants in den Grundzustand E g über. Die Energie des emittierten Photons mit dem Impuls k ist um die Rückstossenergie 2 E p2 2k 2 2 (kc) 2 ER 2 2M Kern 2M Kern 2M Kern c 2M Kern c 2 vermindert. Um einen zweiten Kern mit dem Photon wieder anzuregen, ist die Energie E E R erforderlich (vergleiche mit einem Gas: Die Emissions- und Absorptionslinien sind ebenfalls gegeneinander verschoben). Falls die Linien teilweise überlappen, kann Resonanzabsorption auftreten, d.h. ein Teil der emittierten -Quanten wird von identischen Kernen im Grundzustand absorbiert. Nehmen wir als Beispiel das Isotop Fe57: Hier ist die Linienbreite für die 14.4 keV Linie äusserst klein, 5 10 9 eV. Man erwartet deshalb, dass keine Resonanzarbsorption auftreten kann. Sind die Eisenatome jedoch Teil eines Kristalls, wird der Rückstoss vom gesamten Kristall aufgenommen (wie bei der Braggstreuung), i.e. die Rückstossenergie ist massivst reduziert 68623450 85 ER E 5/15/2016 2 2M Kristallc 2 und Resonanzabsorption wird möglich. Man kann also einen für den Mössbauereffekt massgebenden Debye-Waller Faktor einführen. Wir wollen dies an dieser Stelle nicht tun. In Analogie zum Debye-Waller Faktor für Röntgenstreuung wird der Anteil der rückstossfreien Emission- und Absorption von -Quanten bei tiefer Temperatur am grössten sein. Der Mössbauer Effekt eignet sich zum Studium von zahlreichen Problemen aus der Physik und Chemie. Wir diskutieren hier als Beispiel die Hyperfeinaufspaltung in Fe. Die ungepaarten Elektronen erzeugen am Kernort ein Magnetfeld von der Grössenordnung 4 10 7 A/m. Dadurch wird der Grundzustand mit der Kernspinquantenzahl I 12 in zwei und der angeregte Zustand mit I 32 in vier Zustände aufgespalten. Aufgrund der Selektionsregeln | M | 1 sind sechs Übergänge möglich. Da die Hyperfeinaufspaltung ca. 30 mal grösser ( 10 7 eV) ist als die natürliche Linienbreite , können die einzelnen Übergänge aufgelöst werden. Das Experiment wird wie folgt durchgeführt: Die Quelle enthält das radioaktive Isotop Co57, das in den angeregten Zustand Fe57 zerfällt. Durch die Bewegung der Quelle kann die Frequenz der ausgesandte -Strahlung durch den Dopplereffekt leicht verschoben werden. Wenn die ausgesandte Strahlung eine Frequenz hat, die der Frequenz einer Linie im Grundzustand entspricht, werden die -Quanten absorbiert. Der Detektor zeigt dann ein Minimum in der Zählrate an. Die folgende Figur zeigt ein Messergebnis eine Mössbauerexperiments an einer Probe aus dünnen Schichten von Fe. Manchmal ist auch eine Isomerie-Verschiebung des Linienspektrums sichtbar, die durch die unterschiedliche Ladungsverteilung der Elektronen am Kernort für verschiedene Anregungszustände verursacht wird. 68623450 86 5/15/2016 G. S. Case, M. F. Thomas, C. A. Lucas, D. Mannix, P. Böni, S. Tixier, and S. Langridge, J. Phys.: Condens. Matter 13, 9699 (2001). 3.12. Messung von Phonondispersionsrelationen Phononen in Festkörpern haben typische Wellenzahlen von 2 – 5 Å-1 und Energien von ca. 15 meV. Aus diesem Grund ist es schwierig, mit Röntgen- oder Synchrotronstreuung die Dispersionsrelationen von Phononen zu bestimmen, da für die geeigneten Wellenzahlen die Photonenenergie von der Grössenordnung 10 keV ist. Neutronen sind viel besser geeignet, weil sowohl die Impulse als auch die Energien vergleichbar sind mit Phononenergien. Aus diesem Grund sind alle Dispersionsrelationen von Materialien mit Ausnahme von ganz wenigen Beispielen (Wasser, Quarz) mit Hilfe von Neutronenstreuung bestimmt worden. Im Prinzip sind natürlich die beiden Methoden komplementär, da bei Licht- und Röntgenstreuung die Bewegung der Elektronen gemessen wird, während bei der Neutronenstreuung direkt die Bewegung der Kerne bestimmt wird. In einem typischen Neutronenstreuexperiment beleuchtet man die Probe mit einem monochromatischen Strahl, der durch Braggreflexion an einem Graphitkristall oder Cu Kristall erzeugt wird. Die gestreuten Neutronen werden ebenfalls nach der Energie analysiert und detektiert. Dieses Instrument nennt man “Dreiachsenspektrometer (Monochromator – Probe – Analysator) und ist an fast jedem Forschungsreaktor zu finden. Meistens wird der Analysiatorkristall auf einen fixen Energieübertrag eingestellt und man variiert die Einfallsenergie der Neutronen. Damit sind auch die Beträge der Wellenvektroren der einfallenden und gestreuten Neutronen bestimmt. Durch Wahl des Streuwinkels kann dann der Streuvektor eingestellt werden.