Jahn-Teller Effekt (oder Jahn

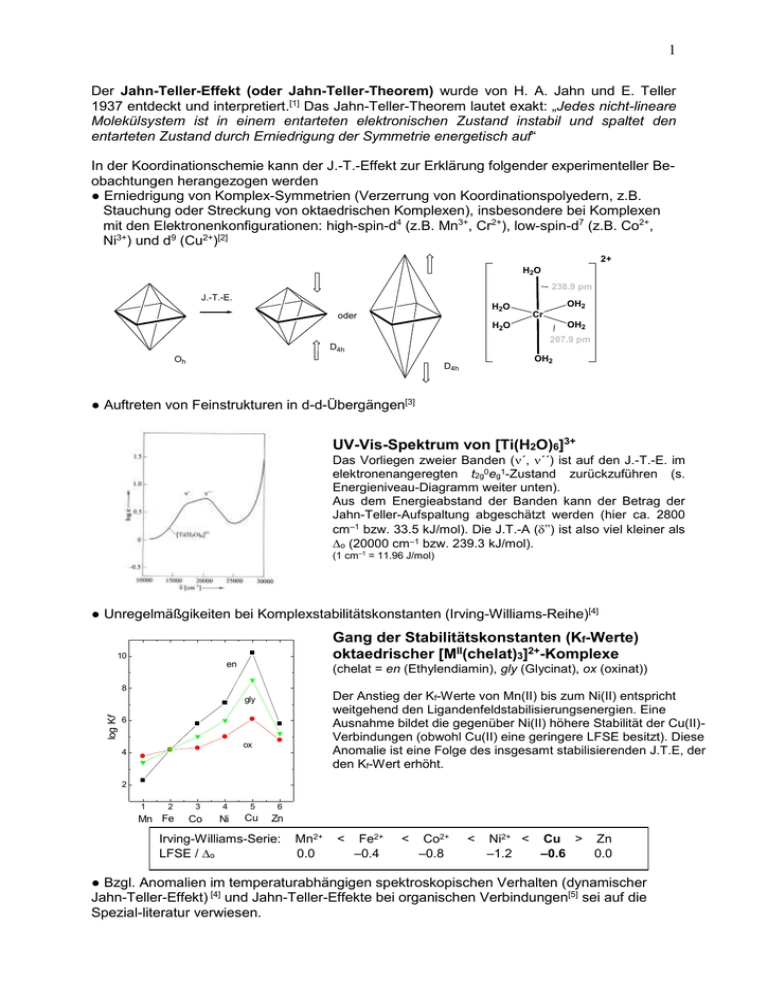
1
Der Jahn-Teller-Effekt (oder Jahn-Teller-Theorem) wurde von H. A. Jahn und E. Teller
1937 entdeckt und interpretiert.[1] Das Jahn-Teller-Theorem lautet exakt: „Jedes nicht-lineare
Molekülsystem ist in einem entarteten elektronischen Zustand instabil und spaltet den
entarteten Zustand durch Erniedrigung der Symmetrie energetisch auf“
In der Koordinationschemie kann der J.-T.-Effekt zur Erklärung folgender experimenteller Beobachtungen herangezogen werden
● Erniedrigung von Komplex-Symmetrien (Verzerrung von Koordinationspolyedern, z.B.
Stauchung oder Streckung von oktaedrischen Komplexen), insbesondere bei Komplexen
mit den Elektronenkonfigurationen: high-spin-d4 (z.B. Mn3+, Cr2+), low-spin-d7 (z.B. Co2+,
Ni3+) und d9 (Cu2+)[2]
2+
H2 O
238.9 pm
J.-T.-E.
H2O
oder
OH2
Cr
OH2
H2O
207.9 pm
D4h
Oh
OH2
D4h
● Auftreten von Feinstrukturen in d-d-Übergängen[3]
UV-Vis-Spektrum von [Ti(H2O)6]3+
Das Vorliegen zweier Banden (´, ´´) ist auf den J.-T.-E. im
elektronenangeregten t2g0eg1-Zustand zurückzuführen (s.
Energieniveau-Diagramm weiter unten).
Aus dem Energieabstand der Banden kann der Betrag der
Jahn-Teller-Aufspaltung abgeschätzt werden (hier ca. 2800
cm–1 bzw. 33.5 kJ/mol). Die J.T.-A (’’) ist also viel kleiner als
o (20000 cm–1 bzw. 239.3 kJ/mol).
(1 cm–1 = 11.96 J/mol)
● Unregelmäßgikeiten bei Komplexstabilitätskonstanten (Irving-Williams-Reihe)[4]
Gang der Stabilitätskonstanten (Kf-Werte)
oktaedrischer [MII(chelat)3]2+-Komplexe
10
en
(chelat = en (Ethylendiamin), gly (Glycinat), ox (oxinat))
8
Der Anstieg der Kf-Werte von Mn(II) bis zum Ni(II) entspricht
weitgehend den Ligandenfeldstabilisierungsenergien. Eine
Ausnahme bildet die gegenüber Ni(II) höhere Stabilität der Cu(II)Verbindungen (obwohl Cu(II) eine geringere LFSE besitzt). Diese
Anomalie ist eine Folge des insgesamt stabilisierenden J.T.E, der
den Kf-Wert erhöht.
log Kf
gly
6
ox
4
2
2
3
4
5
6
Mn Fe
1
Co
Ni
Cu
Zn
Irving-Williams-Serie:
LFSE / o
Mn2+
0.0
<
Fe2+
–0.4
<
Co2+
–0.8
<
Ni2+ < Cu > Zn
–1.2
–0.6
0.0
● Bzgl. Anomalien im temperaturabhängigen spektroskopischen Verhalten (dynamischer
Jahn-Teller-Effekt) [4] und Jahn-Teller-Effekte bei organischen Verbindungen[5] sei auf die
Spezial-literatur verwiesen.
2
Der Jahn-Teller-Effekt ist ein elektronischer Effekt. Gewöhnlich (aber nicht ausnahmslos)
wird der J.-T.-E. beobachtet, wenn die eg- und t2g-Orbitale (bei oktaedrischen Komplexen)
bzw. die e- und t2-Orbitale (bei tetraedrischen Komplexen) weder halb noch ganz besetzt
sind. Der J.-T.-E. ist besonders stark bei oktaedrischen Komplexen bei Besetzung der egOrbitale. Die folgende Tabelle zeigt die Elektronenkonfigurationen, für die der J.-T.-E. zu
erwarten ist (dunkelgrau = starker Jahn-Teller-Effekt,* hellgrau = schwacher Jahn-TellerEffekt). Die Streckung des Oktaeders ist häufiger als die Stauchung (Dehnung von 2
Bindungen (gegenüber 4 Bindungen) ist energetisch günstiger).
oktaedrisches
tetraedrisches
Ligandenfeld
Ligandenfeld
------------------------------------------------------------------------------------------------d0
d1
d2
d3
d4
d5
d6
d7
d8
d9
d10
t2g0
t2g1
t2g2
t2g3
t2g3eg1 (hs)
t2g3eg2 (hs)
t2g4eg2 (hs)
t2g5eg2 (hs)
t2g6eg2
t2g6eg3
t2g6eg4
e0
e1
e2
e2t21 (hs)
e2t22 (hs)
e2t23 (hs)
e3t23 (hs)
e4t23 (hs)
e4t24 (hs)
e4t25 (hs)
e4t26 (hs)
t2g4eg0 (ls)
t2g5eg0 (ls)
t2g6eg0 (ls)
t2g6eg1 (ls)
e3t20 (ls)
e4t20 (ls)
e4t21 (ls)
e4t22 (ls)
------------------------------------------------------------------------------------------------*Strukturelle Auswirkungen des J.-T.-E. sind besonders stark bei Besetzung der eg-Orbitale (Liganden-Orbitale),
aufgrund stärkerer elektrostatischer Wechselwirkungen zwischen den d-Elektronen und Liganden
d-Orbitalenergie
oktaedrisches
Ligandenfeld
d-Orbitalenergie
Jahn-Teller-Effekt
gestrecktes Oktaeder
0.6 o
dx2-y2
1/2 "
eg
Jahn-Teller-Effekt
oktaedrisches
Ligandenfeld
dz2, dx2-y2
gestrecktes Oktaeder
dz2, dx2-y2
0.6 o
-1/2 "
eg
dz2
o
dx2-y2
1/2 "
1/2 "
dz2
''
o
o
dxy, dxz, dyz
dxy
2/3 '
-0.4 o
t2g
'
dxy, dxz, dyz
dxy
-0.4 o
-1/3 '
2/3 '
1/3 '
t2g
dxz dyz
dxz dyz
Energieaufspaltung der d-Zustände eines Zentralatoms
Links: ideales Oktaeder; Rechts: gestrecktes Oktaeder
Bei J.-T.-E. (gestreckt quadratisch-bipyramidal). Für gestauchte
Oktaeder sind die Verhältnisse gerade umgekehrt.
d9
gestrecktes Oktaeder
1/2 "
dx2-y2
-1/2 "
d-Orbitalenergie
Bsp: J.-T.-E. für high-spin-d4 und d9
a) J.-T.-S. t2g4eg0-Konfiguration = ½ ’’
b) J.-T.-S. t2g6eg3-Konfiguration = ½ ’’
d4
d-Orbitalenergie
Jahn-Teller-Stabilisierungsenergie = der mit
der Verzerrung der Polyeder einhergehende
Energiegewinn.
Jahn-Teller-Effekt im elektronenangeregten Zustand von Ti3+
(vgl. das UV-Vis Spektrum oben)
gestrecktes Oktaeder
1/2 "
-1/2 "
dz2
2/3 '
dxy
-1/3 '
dx2-y2
dz2
2/3 '
dxy
-1/3 '
dxz dyz
dxz dyz
3
Ligandenfeld-Theorie
Annahmen
• elektrostatische Wechselwirkungen zwischen Elektronen der Liganden u. Metallionen
• Punktladungen
• Ligandenfeld = elektrisches Feld, das von den Liganden erzeugt wird
Ligandenfeld-Theorie betrachtet energetische Lage der fünf d-Orbitale in einem bestimmten
Kristallfeld:
z
y
x
dx2-y2
dz2
dxy
dxz
dzy
eg-Orbitale
(Orbitallappen auf den Achsen)
t2g-Orbitale
(Orbitallappen zwischen den Achsen)
Abb. 1. Grenzflächendarstellung für die d-Orbitale
Beispiel: Oktaedrischer Komplex
- im oktaedrischen Ligandenfeld: d-Orbitale haben nicht mehr die gleiche Energie
- Liganden weisen direkt auf die dz2- u. dx2-y2-Orbitale (starke elektrost. WW)
- Liganden liegen zwischen den dxy, dxz, dyz-Orbitalen (geringere elektrost. WW)
=> zwei Sätze von d-Orbitalen: t2g- und eg-Orbitale, eg-Orbitale sind energiereicher,
t2g-Orbitale energieärmer, Bezeichnung der Differenz: o Ligandenfeldaufspaltung
Ligand
dxz
dx2-y2
stärkere Abstoßung
Anhebung der Energie
geringere Abstoßung
Absenkung der Energie
Abb. 2. Anordnung der Liganden (kleine Punkte) und Orbitale (hier nur dx2-y2- und dxzOrbitale) in einem oktaedrischen Komplex.
dz2, dx2-y2
eg
Energie
d-Orbitale
0.6 o
o
d-Orbitale
o
0.4 o
kugelsymmetrisches
Ligandenfeld
t2g
dxy, dxz, dyz
isoliertes Ion
oktaedrisches
Ligandenfeld
Abb. 3. Energieniveaudiagramm der d-Orbitale eines Metallions in einem oktaedrischen
Ligandenfeld.
[1] H. Jahn, E. Teller, Proc. R. Soc. London, A 161 (1937), 220.
[2] B. N. Figgis, E. F. Kucharski, P. A. Reynolds, Acta. Cryst. 1990, B46, 577-584.
[3] A. F. Holleman, E. Wiberg, Lehrbuch der Anorganischen Chemie, 102. Aufl., de Gruyter, Berlin
2007, S. 1361 u. 1369.
[4] a) D. F. Shriver, P. W. Atkins, C.H. Langford, Anorganische Chemie, 2. Aufl, Wiley-VCH, 1997,
Weinheim, S. 254. b) ebenda, S. 244, S. 253.
[5] R. Lindner, H. Sekiya, K. Müller-Dethlefs, Angew. Chem. 1993, 105, 1384–1387.