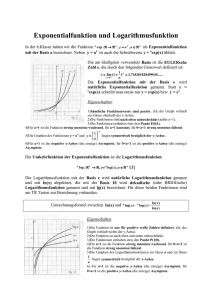
Exponentialfunktionen und Logarithmusfunktionen

Zusammenfassung: Klasse 10: Potenzen,
Logarithmen, Exponentialfunktionen und
Logarithmusfunktionen / Umkehrfunktionen
Von Florian Modler
Inhalt
1 Potenzen
1.1 Potenzgesetze
1.2 Wurzeln
2 Logarithmen
2.1 Logarithmusgesetze
2.2 Exponentialgleichungen
3 Exponentialfunktionen
3.1 Berechnungen y=ax
3.2 Berechnungen y=bax
4 Logarithmusfunktionen
4.1 Berechnungen
5 Umkehrfunktionen
1 Potenzen
a n  a  a  a  ...  a
nFaktoren
a1  a
a0  1
a 1 
1
a
1.1 Potenzgesetze
an
 a nm
am
p
a
p
p
p a
a  b  (ab) ; p  ( ) p
b
b
n m
nm
(a )  a
a n  a m  a nm ;
n
m
an  a m
Beispiele:
1
34 34
1
 7  4 7
7
5
5
3 5
4
4
3
3

 34  57
7
1
5
57
34 57

57 34
1.2 Wurzeln
n
m
an  a m
3
11  11  113 112  113
1
1
1 1

2
5
 116  6 115
Radizieren: 3 16  3 2³  2  3 2³  2  2  2
Nenner rational machen:
1
5
5


5
5
5 5
2 Logarithmen
ax  b
a : Basis
x : Exponent
 log a b  x
a : Basis
x : Exponent
Logarithmen sind Exponenten
Beispiele:
2x=0,5
x=log20,5
5x=125
x=log5125=3
log28=x
2x=8
x=3
log464=x
4x=64
; x=3
2.1 Logarithmusgesetze
log a (uv)  log a u  log a v
u
 log a u  log a v
v
log a vt  t  log a v
log a
log a x 
lg x
lg a
Beispiele:
3
lg( x )³  lg x 2 
3
 lg x
2
u
v³
2 lg 5  lg 3  lg 5²  lg 3  lg 25  lg 3  lg(25  3)  75
lg u  3lg v  lg u  lg v ³  lg
1) Berechne x:
1
log a ( x)  2 log a u  log a v
2
1
log a ( x)  log a u ²  log a v 2
1
2
log a ( x)  log a (u ²  v )
1
2
x  u²  v  u²  v
2.2 Exponentialgleichungen
1. Beispiel:
Schreibe 32 als Zweierpotenz. Löse so 23 x1  32 durch „Vergleichen der Exponenten“.
23 x 1  32
23 x 1  25
3x  1  5
x2
2. Beispiel:
Löse: 1, 24 x7  9 .
1, 24 x 7  9 | lg
lg1, 24 x 7  lg 9
(4 x  7)1, 2  lg 9
lg 9
7
lg12
x
4
3. Beispiel:
Berechne:
7 x 1  3  5 x | lg
lg 7 x 1  lg 3  lg 5 x
( x  1) lg 7  lg 3  x lg 5
x lg 7  lg 7  lg 3  x lg 5 |  x lg 5  lg 7
x lg 7  x lg 5  lg 3  lg 7
x[lg 7  lg 5]  lg 3  lg 7 |: lg 7  lg 5
lg 3  lg 7
x
lg 7  lg 5
4. Beispiel:
Löse: 5  5x  5 x  6
5  5 x  5 x  6
5x  u
1
5u   6
u
5u ²  6u  1  0 |: 5
u ²  1, 2u  0, 2
u  0undu  1
3 Exponentialfunktionen
Exponentialfunktionen und
Logarithmusfunktionen
1. Exponentialfunktionen
Definition:
Die Funktion f mit f ( x)  b x (b   /{1}) heißt Exponentialfunktion zur Basis b.
Die Einschränkung (b   /{1}) muss vorgenommen werden, da 1. die Funktion f(x)=1x der
Funktion y=1 entspricht und somit eine Gerade ist und 2. b   , weil die Funktion mit einem
negativen b nicht stetig wäre, sie würde „hin und her springen“, da für positive x-Werte der yWert positiv wird, aber für negative x-Werte der y-Wert negativ wird.
Auch die Funktion f ( x)  a  b x (mit a  0 ) heißt Exponentialfunktion.
Einschränkung muss vorgenommen werden, da für a=0 die Funktion y=0 lauten würde.
Die Zahl a heißt Anfangswert der Funktion f und gibt an, wo der Graph der Funktion
die y-Achse schneidet.
Eigenschaften:
1
(1) Der Graph der Exponentialfunktion f ( x )  ( ) x geht aus dem Graphen g ( x)  b x durch
b
Spiegelung an der y-Achse hervor.
(2) Die x-Achse ist Asymptote der Graphen von f und g.
(3) Der Graph der Funktion g ( x)  b x ist streng monoton steigend für b>1 und streng
monoton fallend für 0<b<1.
(4) Der Wertebereich von f ist 
3.1 Berechnungen y=ax
1) Bestimme die Exponentialfunktion f(x)=ax, deren Graph durch P (3/5) geht.
f ( x)  a x ; P(3 / 5)
5  a ³ | 3 ...
a35
f ( x)  ( 3 5) x
2) Wie ändert sich der Funktionswert f(x) von f ( x)  3x , wenn x um d zunimmt?
f ( x)  3x  d  3x  3d
3.2 Berechnungen y=bax
1) Bestimme a und b so, dass der Graph von f(x)=bax durch (-1/24) und (1,5/07,5) geht.
- Einsetzen der Punkte: b  a 1  24undb  a1,5  0,75
b  a 1  24
1
- Auflösen der 1. Gleichung : b   24
a
b  24a
- Einsetzen von b in die 2. Gleichung:
24a  a1,5  0, 75
3
24  a  a 2 
3
|: 24
4
1
32
1 52 1
a( ) 
32
4
a 2,5 
2) Schreibe f ( x)  23 x 5 in f(x)=bax um.
f ( x)  23 x 5  (2³) x  25  32  8x
4 Logarithmusfunktionen
Definition:
Für x   und b>1 ist der Logarithmus log b x zur Basis b diejenige Hochzahl, mit der man
b potenzieren muss, um x zu erhalten.
f ( x)  logb x heißt Logarithmusfunktion zur Basis b.
Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion.
Eigenschaften:
(1) Die y-Achse ist Asymptote von f ( x)  logb x (mit b>1; x   )
(2) f ist streng monoton steigend.
(3) Der Wertebereich ist ; der Definitionsbereich dagegen  .
(4) f hat die Nullstelle bei (1; 0)
Satz 6:
Es gilt:
(1)blogb x  x; x 

(2) logb b y  y; y 
Anders ausgedrückt: y  logb x ist äquivalent zu x  b y .
Satz 7:
log b ( x1  x2 )  log b x1  log b x2
log b (
x1
)  log b x1  log b x2
x2
log b ( x t )  t  log b x
5 Umkehrfunktionen
- Graphischer Weg, um Umkehrfunktion zu bestimmen:
Man spiegelt den Graphen an der Winkelhalbierenden y=x.
- Rechenweg:
Rechnerisch bestimmt man die Umkehrfunktion, indem man x und y vertauscht.
Denn die Definitionsmenge der Funktion ist die Wertemenge der Umkehrfunktion und die
Wertemenge der Funktion ist der Definitionsbereich der Umkehrfunktion!
y  x² |
x  y ² | ...
y x
Satz 5:
Wenn eine Funktion streng monoton steigend [fallend] ist, so ist sie umkehrbar.