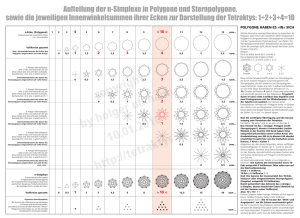
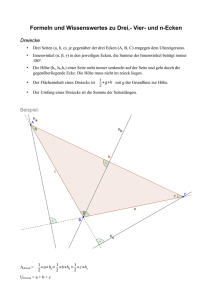
doc

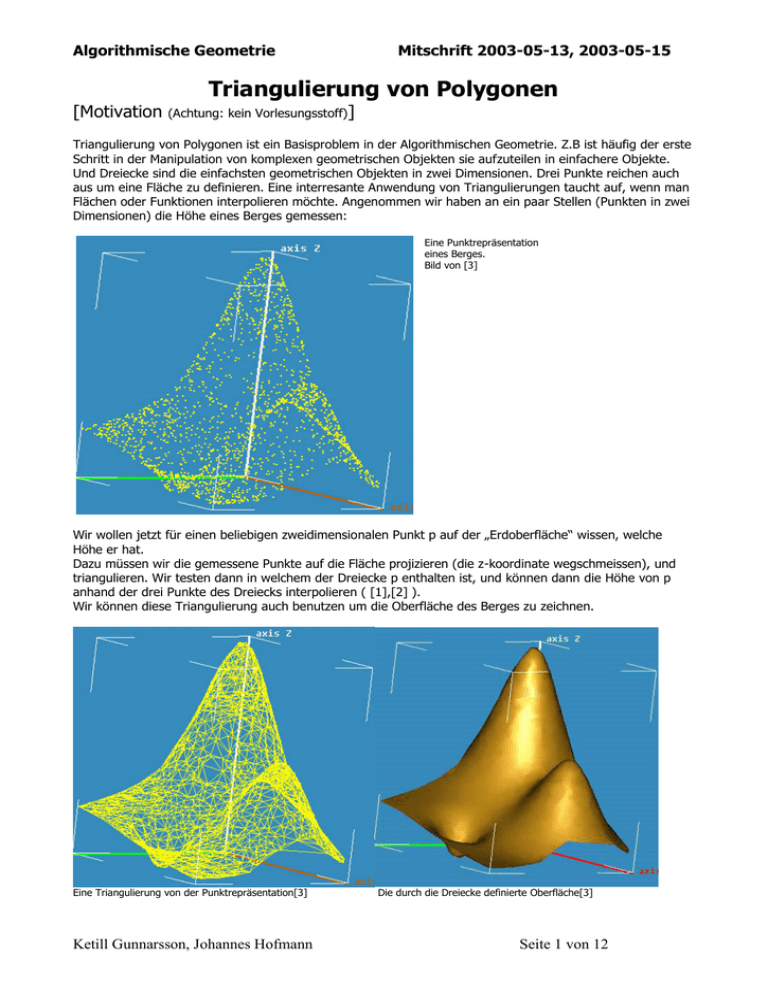
Algorithmische Geometrie
[Motivation
Mitschrift 2003-05-13, 2003-05-15
Triangulierung von Polygonen
(Achtung: kein Vorlesungsstoff)]
Triangulierung von Polygonen ist ein Basisproblem in der Algorithmischen Geometrie. Z.B ist häufig der erste
Schritt in der Manipulation von komplexen geometrischen Objekten sie aufzuteilen in einfachere Objekte.
Und Dreiecke sind die einfachsten geometrischen Objekten in zwei Dimensionen. Drei Punkte reichen auch
aus um eine Fläche zu definieren. Eine interresante Anwendung von Triangulierungen taucht auf, wenn man
Flächen oder Funktionen interpolieren möchte. Angenommen wir haben an ein paar Stellen (Punkten in zwei
Dimensionen) die Höhe eines Berges gemessen:
Eine Punktrepräsentation
eines Berges.
Bild von [3]
Wir wollen jetzt für einen beliebigen zweidimensionalen Punkt p auf der „Erdoberfläche“ wissen, welche
Höhe er hat.
Dazu müssen wir die gemessene Punkte auf die Fläche projizieren (die z-koordinate wegschmeissen), und
triangulieren. Wir testen dann in welchem der Dreiecke p enthalten ist, und können dann die Höhe von p
anhand der drei Punkte des Dreiecks interpolieren ( [1],[2] ).
Wir können diese Triangulierung auch benutzen um die Oberfläche des Berges zu zeichnen.
Eine Triangulierung von der Punktrepräsentation[3]
Ketill Gunnarsson, Johannes Hofmann
Die durch die Dreiecke definierte Oberfläche[3]
Seite 1 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
[Das Museumsproblem]
Ein weiteres Triangulierungsproblem ist das sogenannte Museumsproblem ( Art Gallery Problem ). Ein
Museum soll mit Kameras überwacht werden. Wir wollen wissen, wie viele Kameras wir benötigen und wo
die Kameras platziert werden sollen (Die Kameras werden auch Wächter genannt).
Ein Museum mit Kameras [4]
Überdeckung einer Kamera als Punktlichtquelle [4]
Definitionen:
- Der Plan des Museums ist ein einfaches Polygon P mit n Ecken
- Eine Kamera ist ein Punkt k (eine Punktlichtquelle)
- Eine Kamera sieht einen Punkt p genau dann, wenn die Strecke kp ganz
im Inneren von P liegt.
Also:
Wie viele Kameras müssen in P platziert werden, damit jeder Punkt im Inneren von P gesehen wird?
Idee:
Zerlege P in Stücke, die jeweils mit einer Kamera bewacht werden können, entweder:
- beliebige konvexe Stücke
- Dreiecke
Ein konvexes Polygon
(und damit auch ein Dreieck)
kann immer mit einer Kamera
bewacht werden.
(Bild von [4] ).
Leider ist das Problem, die kleinste Anzahl von Kameras zu einem gegebenen Polygon P zu finden, NPschwer. Wir fragen uns deswegen, wie viele Kameras immer ausreichen, um ein Polygon mit n Ecken zu
bewachen.
Eine einfache Lösung:
- Das Polygon triangulieren, und in jedes Dreieck eine Kamera stellen (s. Kapitel über Trianglulierung).
Ergibt n-2 Dreiecke -> n-2 Kameras reichen aus (siehe unten).
Eine bessere Lösung:
- Wähle eine Eckenmenge W aus P, s.d. jedes Dreieck mindestens eine Ecke in W hat.
- Platziere Kameras auf diese Ecken.
Aus 3-Färbbarkeit von Triangulierungen folgt (Satz):
Satz: Jedes einfache Polygon P mit n Ecken kann mit n/3 Kameras bewacht werden
Beweis:
- Finde eine 3-Färbung einer Triangulierung von P
- Wähle die kleinste Farbklasse als Menge der Kameras
- Die kleinste Farbklasse hat höchstens n/3 Elemente
Ketill Gunnarsson, Johannes Hofmann
Seite 2 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
Satz: Es gibt Polygone mit n Ecken, für die man n/3 Kameras benötigt.
Beweis:
[ Triangulierungen – Definition und Existenz ]
Definition:
-
Eine Diagonale eines einfachen Polygons P ist eine offene Strecke zwischen zwei Ecken von P, die
ganz Im Inneren von P liegt.
Definition:
-
Eine Triangulierung eines einfachen Polygons P ist eine Zerlegung von P in Dreiecke, welche von
einer maximalen Menge von paarweise disjunkten Diagonalen induziert wird.
Eine maximale Menge von disjunkten Diagonalen impliziert, dass keine Ecken auf dem Rand eines Dreiecks
liegen können.
Zu einem Polygon gibt es i. allg. Verschiedene Triangulierungen !
Zwei verschiedene
Triangulierungen eines Polygons
Fragen über Triangulierungen:
- Gibt es zu jedem einfachen Polygon eine Triangulierung?
- Wie viele Dreiecke braucht man, um ein Polygon zu triangulieren?
Existenz von Triangulierungen:
Satz: Zu jedem einfachen Polygon P gibt es eine Triangulierung.
Beweis:
Zeigen durch Induktion über n, dass jedes einfache Polygon P trianguliert werden kann.
I.A.: (n=3): Dann ist P ein Dreieck.
I.S.: Sei P ein einfaches Polygon mit n Ecken. Wir zeigen zunächst, dass es in P eine Diagonale gibt.
Sei v die lexikographisch kleinste Ecke von P und u sowie w die zu v adjazenten Ecken von P.
Fall 1.)
Die Strecke uw liegt in P uw ist eine Diagonale
Ketill Gunnarsson, Johannes Hofmann
Seite 3 von 12
Algorithmische Geometrie
Fall 2.)
Mitschrift 2003-05-13, 2003-05-15
Die Strecke uw schneidet den Rand von P uw ist keine Diagonale. Dann gibt es mindestens eine
Ecke von P auf uw oder in dem Dreieck uvw. Sei v‘ die Ecke von P in dem Dreieck uvw die am
weitesten von der Strecke uw entfernt ist. Die Strecke vv‘ schneidet keine Kante von P; sonst hätte
diese einen Endpunkt innerhalb von uvw der weiter von uw entfernt wäre als v‘ vv‘ ist eine
Diagonale.
In P gibt es also eine Diagonale. Diese zerlegt P in zwei Polygone L und R mit l bzw. r Ecken, wo l<n und
r<n. Nach I.V. kann jedes einfache Polygon mit n‘<n Ecken trianguliert werden, also ibs. L und R. Damit
kann auch P trianguliert werden.
q.e.d.
Grösse von Triangulierungen:
Satz: Jede Triangulierung eines einfachen Polygons mit n Ecken besteht aus n-2 Dreiecken.

Beweis:
Zeigen durch Induktion über n, dass jede Triangulierung eines einfachen Polygons mit n Ecken aus n-2
Dreiecken besteht.
I.A.: (n=3) Dann ist P ein Dreieck, 1=3-2
I.S. : Sei P ein einfaches Polygon mit n Ecken und T eine Triangulierung von P. Sei d eine Diagonale von P
aus T, die P in zwei Polygone L und R mit l bzw. r Ecken zerlegt, wobei l<n und r<n. Die Ecken von d
gehören zu L und R, also n+2=l+r. Nach I.V. hat jede Triangulierung von L bzw. R l-2 bzw. r-2 Dreiecke.
Damit hat die T gerade (l-2)+(r-2)=n-2 Dreiecke.
Färbung von Graphen:
Definition:
-
Eine Färbung eines Graphen G=(V,E) ist eine Funktion, die jedem Knoten aus V eine Farbe
zuordnet, mit der Eigenschaft, dass die Endpunkte jeder Kante aus E dabei unterschiedliche Farben
haben.
Definition:
-
Sei k > 0 eine natürliche Zahl. Eine k-Färbung eines Graphen G=(V,E) ist eine Färbung von G mit
höchstens k Farben.
Ketill Gunnarsson, Johannes Hofmann
Seite 4 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
3-Färbbarkeit von Triangulierungen:
Satz: Der Graph einer Triangulierung T eines einfachen Polygons P ist 3-färbbar.
Beweis:
Durch Induktion über n.
I.A. : (n=3) Dann ist P ein Dreieck und damit 3-färbbar.
I.S. : Sei P ein einfaches Polygon mit n Ecken und T eine Triangulierung von P. Sei d=(a,b) eine Diagonale
aus T.
d zerlegt T in zwei Triangulierungen L und R einfacher Polygone mit je < n Ecken.
Nach i.V. sind L und R 3-färbbar.
Die Ecken a und b von d gehören zu L und R falls diese Ecken unter den Färbungen von L und R
verschiedene Farben erhalten haben, müssen die Farben von L entsprechend permutiert werden.
Ketill Gunnarsson, Johannes Hofmann
Seite 5 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
Monotone Polygone
Eine Methode zum Triangulieren von Polygonen ist, die Polygone erstmal in monotone Polygone zu zerlegen
und die monotone Polygone einzeln zu triangulieren.
Definition:
-
Ein Polygon P heisst monoton bezüglich einer Geraden l, wenn der Durchschnitt des Inneren von P
mit jeder Geraden die parallel zu l ist, zusammenhängend ist.
Definition:
-
Ein Polygon P heisst y-monoton, wenn es monoton bezüglich der x-Achse ist.
Definition:
-
P heisst streng y-monoton, wenn es in P keine horizontale Kante gibt.
Eigenschaften y-monotoner Polygone:
Wenn ein Polygon P monoton bezüglich einer Geraden l ist, dann ist der Schnitt des Inneren von P mit
jeder Geraden die parallel zu l ist, entweder:
- leer
- Ein Punkt
- Eine Strecke
Wenn man sich auf der linken (rechten) Seite eines y-monotonen Polygons P vom höchsten zum tiefsten
Eckpunkt von P bewegt, so bewegt man sich immer horizontal oder nach unten (aber nie nach oben). Wenn
man sich auf einer Seite eines streng y-monotonen Polygos vom höchsten zum tiefsten Eckpunkt bewegt,
so bewegt man sich immer nach unten.
Streng y-Monoton: Immer nach unten.
Ketill Gunnarsson, Johannes Hofmann
Seite 6 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
Zerlegung in y-monotone Polygone:
Wir überstreichen ein Polygon P mit einer horizontalen Gerade und betrachten den Schnitt der Geraden l mit
dem Inneren von P. Dieser Durchschnitt ist eine Menge von Intervallen auf l .
Bei den
-
-
Ecken von P können Intervalle:
neue entstehen (Start-Ecken)
verschwinden (End-Ecken)
verschmelzen (Merge-Ecken)
in zwei Teile zerfallen ( Split-Ecken)
(kombinatorisch) unverändert bleiben (reguläre Ecken)
Klassifikation von Ecken:
Eine Ecke p von P ist eine:
- Start-Ecke gdw. die Nachbarn liegen unterhalb von p, und der innere Winkel bei p ist < 180
- End-Ecke gdw. die Nachbarn liegen oberhalb von p, und der innere Winkel bei p ist < 180
- Merge-Ecke gdw. die Nachbarn liegen oberhalb von p, und der innere Winkel bei p ist > 180
- Split-Ecke gdw. die Nachbarn liegen unterhalb von p, und der innere Winkel bei p ist > 180
- Alle anderen Ecken sind reguläre Ecken
Charakterisierung y-monotoner Polygone (Satz):
Satz: Ein einfaches Polygon P ist y-monoton gdw. es keine Split- und keine Merge-Ecken hat.
Beweis:
Wir zeigen: P ist nicht y-monoton es gibt eine Split- oder Merge-Ecke.
Sei also P nicht y-monoton es gibt eine horizontale Gerade l deren Schnitt mit P aus mindestens zwei
Intervallen besteht. Betrachte das linkeste Intervall pq mit linkem Endpunkt p und rechtem Endpunkt q.
Durchlaufe von q aus den Rand von P so, dass P links liegt.
Sei r der erste Punkt, der wieder auf der Geraden l liegt
Fall 1: r p
Die höchste Ecke der wir auf dem Weg von q nach r
begegnet sind, muss eine Split- Ecke gewesen sein
Fall 2: r = p
Durchlaufe von q aus den Rand von P so, dass P rechts liegt;
sei r‘ der erste Punkt, der wieder auf der Geraden l liegt.
r‘ p da ansonsten P nur zwei Schnittpunkte mit l hätte.
Die tiefste Ecke der wir auf dem Weg von q nach r‘ begegnet sind,
muss somit eine Merge-Ecke gewesen sein.
Aus der definition von Split- oder Merge-Ecken folgt:
Es gibt eine Split- oder Merge-Ecke  P ist nicht y-monoton.
Ketill Gunnarsson, Johannes Hofmann
Seite 7 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
DCEL- Doubly Connected Edge List
- Eine Datenstruktur für ebene Unterteilungen -
Anwendungsbeispiel:
DCEL ist z.B geignet um Überlappungen von Karten zu berechnen. Man könnte sich vorstellen eine Karte mit
Bevölkerungsdichte-Informationen und eine Karte mit Storchpopulationsinformationen zu überlappen, um zu
überprüfen, wie sich die zwei Grössen zu einander verhalten. In der DCEL werden in diesem Fall die
Unterteilung der Karte in verschiedene Unterregionen gespeichtert.
DCEL Struktur:
Die DCEL-Struktur besteht aus einer Sammlung von drei verschiedenen Arten von Einträgen:
(Hier nur eine Übersicht, genauere Erläuterung folgt später.)
- Knoten:
Jeder Knoten speichert seine Koordinate und einen Verweis auf seine inzidente Halbkante. Diese Kante ist
eine beliebige Halbkante die den Knoten als Ursprung hat. Zusätzlich können noch benötigte
Attributinformationen gepeichert werden (z.B Farbe,...).
- Facetten:
Jede Facette speichtert einen Verweis auf eine Halbkante ihrer äusseren Begrenzung, sowie eine Liste von
Verweisen auf Halbkanten von inneren Löchern(eine Halbkante pro Loch).
- Halbkanten:
Jede Halbkante speichert ihren Ursprungsknoten, ihre Zwillingshalbkante, ihre inzidente Facette sowie
Verweise auf ihre Vorgänger-und Nachfolgerhalbkante)
Unterstüzte Operationen:
- inzidente Kanten einer Facette zyklisch durchlaufen
- von einer Facette f über eine Kante e von f zur zweiten, zu e adjazenten Facette gehen
- inzidente Kanten einer Ecke zyklisch durchlaufen
- Einfügen von Ecken auf (= unterteilen von) Kanten
- Einfügen von Kanten zwischen Ecken (= Spalten von Facetten)
Platzbedarf O(Komplexität der ebenen Unterteilung).
Bemerkung: Isolierte Ecken werden von dieser Datenstruktur nicht unterstützt. Man kann dies jedoch
unterstützen, indem man zu jeder isolierten Ecke eine Kante zu sich selbst hinzufügt.
Darstellung von Kanten in der DCEL
- die Kante e mit den Ecken p,q wird dargestellt durch die beiden (orientierten) Halbkanten
h(e)=(p,q) und h‘(e)=(q,p)
- h‘ heisst der Zwilling von h (und umgekehrt)
- p heisst der Anfang von h, q heisst das Ende von h
- falls g=(r,p) und h=(p,q), so heissen g und h aufeinanderfolgend (i.allg. gibt es mehrere Halbkanten
die auf g folgen)
Ketill Gunnarsson, Johannes Hofmann
Seite 8 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
-
die Facette F „links“ von h heisst die Facette von h
-
der Eintrag für eine Halbkante h=(p,q) speichert
einen Zeiger AnfangsEcke(h) auf den Eintrag für
die Ecke p
einen Zeiger ZwillingsKante(h) auf den Eintrag für die Halbkante h‘=(q,p)
einen Zeiger Facette(h) auf den Eintrag für die Facette von h
einen Zeiger NachfolgerKante(h) auf den Eintrag für den Nachfolger von h
einen Zeiger VorgängerKante(h) auf den Eintrag für den Vorgänger von h
-
Darstellung von Facetten in der DCEL
- eine Facette F wird durch eine Menge von Randfolgen dargestellt
- eine Randfolge R von F ist eine maximale zyklische Folge von paarweise verschiedenen, jeweils
aufeinanderfolgenden, Halbkanten von F
- die Halbkanten einer Randfolge R durchlaufen den Rand der zugehörenden Facette
- geschieht dies gegen den Uhrzeigersinn, so heisst R äusserer Rand, ansonsten innerer Rand von F
- „Rand“ := Randfolge
-
-
jede beschränkte Facette hat genau einen äusseren Rand
die Anzahl der inneren Ränder von F entspricht der Anzahl der Löcher von F (im
graphentheoretischen Sinn)
jede Halbkante h gehört zu genau einem Rand
die Ränder verschiedener Facetten sind disjunkt
die Ränder einer Facette sind disjunkt
wenn F die Facette von h ist, so gehört h zu einer der Randfolgen von F
jede Halbkante hat somit einen eindeutig bestimmten Vorgänger und Nachfolger
Ketill Gunnarsson, Johannes Hofmann
Seite 9 von 12
Algorithmische Geometrie
-
Mitschrift 2003-05-13, 2003-05-15
der Eintrag für eine Facette f speichert
einen Zeiger AussenKante(f) auf den Eintrag einer beliebigen Halbkante auf dem äusseren Rand
von f
eine Liste InnenKanten(f), die für jeden inneren Rand R von f einen Zeiger auf den Eintrag
einer beliebigen Halbkante von R speichert
Darstellung von Ecken (Knoten):
- der Eintrag für eine Ecke p=(x,y) speichert
- die Koordinaten (x,y) von p
- einen Zeiger InzidenteHalbkante(p) auf den Eintrag einer beliebigen, zu p inzidenten
Halbkante, deren Anfang p ist
Ketill Gunnarsson, Johannes Hofmann
Seite 10 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
Operationen:
inzidente Halbkanten einer Facette f zyklisch durchlaufen
-
-
zyklisches Durchlaufen der Halbkantenliste ausgehend von AussenKante(f) über
NachfolgerKante() (Durchlauf des äusseren Randes von f gegen den Uhrzeigersinn)
für jeden Zeiger h auf eine Halbkante in InnenKanten(f) zyklisches Durchlaufen der
Halbkantenliste ausgehend von h über NachfolgerKante() (Durchlauf der inneren Ränder
von f im Uhrzeigersinn)
O(1) Zeit pro Kante
von einer Facette f über eine Halbkante h von f zur gegenüberliegenden (= zu h‘ adjazenten) Facette f‘
gehen
-
Facette(ZwillingsKante(h)) zeigt auf den Eintrag für die Facette f‘
O(1) Zeit pro Operation
inzidente Kanten einer Ecke p zyklisch durchlaufen
-
starte bei InzidenteHalbkante(p)
-
der Nachfolger einer Halbkante h in der
zyklischen Ordnung um p ist
NachfolgerKante(ZwillingsKante(h))
Durchlauf erfolgt im Uhrzeigersinn
O(1) Zeit pro Kante
-
Einfügen einer Ecke r auf einer Halkante h=(p,q)
-
erzeuge eine neue Halbkante k und ihren Zwilling k‘ (als Kopie von h bzw. h‘)
setze InzidenteHalbkante(q) auf k‘
setze InzidenteHalbkante(r) auf k
setze AnfangsEcke(k) auf r
setze AnfangsEcke(h‘) auf r
setze NachfolgerKante(h) auf k
setze VorgängerKante(h‘) auf k‘
setze VorgängerKante(k) auf h
setze NachfolgerKante(k‘) auf h‘
O(1) Zeit pro Operation
Ketill Gunnarsson, Johannes Hofmann
Seite 11 von 12
Algorithmische Geometrie
Mitschrift 2003-05-13, 2003-05-15
Einfügen einer Kante zwischen zwei Ecken p,q einer Facette f ohne innere Ränder
-
Verzeigerung der zu p,q inzidenten Halbkanten von f anpassen*
Facette()-Zeiger der Halbkanten auf der kleineren Facette anpassen
O(Komplexität der kleineren Facette) Zeit
p
q
*Wenn von p bzw. q viele HalbKanten ausgehen, können wir nicht über den zu p bzw. q inzidenten Kante
einen eindeutigen Nachfolger-und Vorgänger von unsere eingefügte Strecke holen. Eine Lösung ist dass man
davon ausgeht das man schon beim einfügen die richtige Nachfolger-und Vorgängerkanten übergeben
bekommt.
p
q
Eine von diesen Halbkanten ist die
zu q inzidente Halbkante. Ist der
unsere richtige Nachfolger bzw.
Vorgängerkante?
[1] The Algorithm Design Manual by Steven S. Skiena, Steve SkienaTelos Pr; Book and CD-ROM edition
(November 14, 1997), ISBN: 0387948600.
[2] http://www.cs.sunysb.edu/~algorith/files/triangulations.shtml , Computer Science Department at Stony
Brook University. Link besucht am 2003-05-16.
[3] http://herakles.zcu.cz/~miva/research/crust.html, Ivana Koligerová ([email protected]) Michal
Varnuška ([email protected]), Centre of Computer Graphics and Data Visualisation, Department of
Computer Science and Engineering, University of West Bohemia, Plzen, Czech Republic. Link besucht am
2003-05-16.
[4] Computational Geomety, Mark de Berg, Marc von Kreveld, Mark Overmars, Otfried Schwarzkopf,
ISBN 3 –540-65620-0.
Ketill Gunnarsson, Johannes Hofmann
Seite 12 von 12