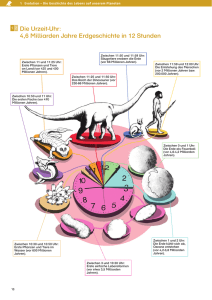
Diskretes exponentielles Wachstum

Diskretes exponentielles Wachstum
Bsp.: aus Tim_Lechner 2
5.22 In einem Land wächst der Stromverbrauch jährlich um 3%. Anfänglich, d.h. zur Zeitt t=0 Jahre,
betrug er 60 000 GWh (GigaWattstunden). Wie lautet die Gleichung der
Stromverbrauchsfunktion y = c· a t für t in Jahren?
5.25 Das Edelgas Radon ist radioaktiv; Radon-Atomkerne (genauer solche mit 222 Kernteilchen)
zerfallen unter Aussendung eines α-Teilchens in das Element Polonium. Sind anfänglich
beispielsweise No = 1014 Radon-Atomkerne vorhanden, so ist ihre Anzahl nach t Tagen gegeben
t
durch N(t) = N0  e
, wobei λ= 0,1812 ist.
a) Wie viele Kerne sind nach 2 Tagen noch nicht zerfallen?
b) Ermittle die Halbwertszeit τ. Wie viele Radon-Kerne sind also nach Ablauf von τ Tagen
noch vorhanden?
c) Wie groß ist die Abnahmerate pro Tag?
5.26 Von einem radioaktivem Stoff zerfallen pro Minute 40%. Anfänglich waren 100 mg vorhanden.
Wie viel sind nach 1, 2, 4, 5 Minuten noch vorhanden?
5.27 Mit Hilfe des radioaktiven Kohlenstoffs C 14 (Halbwertszeit 5730 Jahre) ist es möglich, das Alter
von Fossilien zu bestimmen. C 14 befindet sich in einem geringen Ausmaß im Kohlendioxid der
Luft und wird über die pflanzliche Nahrung und die Atemluft in den Organismus aufgenommen.
Diese laufende Aufnahme einerseits und der Zerfall andererseits führen zu einer bestimmten
festen Menge von C 14 im lebenden Organismus. Im Zeitpunkt des Todes endet jedoch die C-14Aufnahme, es findet nur mehr der Zerfall statt.
a) Wie viel Prozent der ursprünglichen C-14-Menge sind nach 5000 Jahren in einem Fossil noch
vorhanden?
b) In einem fossilen Knochen ist noch 20% der
ursprünglichen C-14-Menge vorhanden. Wie alt ist der Knochen?

h
5.28 Die so genannte barometrische Höhenformel p = 1013  e 7991 gibt für die "Normatmosphäre" die
Abnahme des Luftdrucks in Millibar (mbar) mit zunehmender Höhe h in m über dem Meeresniveau an
a) Wie viel Prozent des Luftdruckes auf Meeresniveau beträgt der Luftdruck am Gipfel des
Großglockners (3798m).
b) Berechne die "Halbwertshöhe" des Luftdrucks, also die Höhe, in der sich der Luftdruck halbiert
hat.
c) In welcher Höhe ist der Luftdruck nur mehr 40 % des Luftdruckes auf dem Meeresniveau?
5.29 Auf Grund der Absorption kann Sonnenlicht nicht in größere Meerestiefen eindringen. Besonders
stark wird rotes Licht absorbiert. Ist y0 dessen Intensität an der Meeresoberfläche, so beträgt die
Intensität y(x) in einer Tiefe x in Metern: y(x) = y 0  e 2,4x
Berechne die "Halbwertstiefe" für rotes Licht in Wasser.
5.31 Koffein hat eine Halbwertszeit von etwa 7 Stunden. Jemand trinkt um drei Uhr Nachmittag 2
Tassen Kaffee.
a) Welchen Koffeingehalt (ausgedrückt in Tassen) hat er um 22 Uhr im Blut?
b) Wie lautet die Antwort, wenn er um 17 Uhr eine weitere Tasse Kaffee trinkt?
5.32 Aspirin ist ein vielfach verwendetes schmerzstillendes Mittel. Sein Wirkstoff Acetyl-salicylsäure
wird mit einer Halbwertszeit von etwa 3 Stunden ausgeschieden. Eine handelsübliche Tablette
enthält 320 mg dieses Wirkstoffes. Ein Patient nimmt um 6 Uhr 2 Tabletten, um 12 Uhr und um
18 Uhr je eine weitere.
Wieviel Wirkstoff befindet sich um 22 Uhr im Körper des Patienten?
5.33 Eine Bakterienkultur vermehrt sich exponentiell; man stellt fest, dass ihre Anzahl in drei Minuten
von 4 auf 15 angewachsen ist. Wie hoch ist die Wachstumsrate pro Minute?
5.34 In einem Wald wurde seit dem Jahre 1980 kein Holz gefällt. Bis zum Jahr 2000 hat sich der
Bestand auf etwa 48 000 fm erhöht. Erfahrungsgemäß wächst der Holzbestand jährl um 2%.
a) Wie lautet das Wachstumsgesetz für den Holzbestand bei Annahme eines exponentiellen
Wachstums?
b) Wie groß ist der Holzbestand im Jahre 2010? In diesem Jahr werden 15000 Festmeter gefällt.
Wann wird wieder der Bestand des Jahres 2010 erreicht?
5.36 In einem Land wächst die Bevölkerung in einem Jahr von anfänglich 10 Mio. Einwohnern auf
10,20 Mio. Gib die Bevölkerungszahlen nach 2, 3, 4, 5 und 10 Jahren an, wenn a) eine lineare
Zunahme, b) eine exponentielle Zunahme angenommen wird.
5.37 Eine Stadt, die zur Zeit 140000 Einwohner hat, verliert im Mittel jährlich 1 % ihrer Einwohner.
a) Stelle die Abnahme der Einwohnerzahl rekursiv dar.
b) Wie lautet die Termdarstellung für die Einwohnerzahlen? Wie groß ist ihre Einwohnerzahl in
10 Jahren?
5.38 Die Weltbevölkerung hat in den folgenden Jahren jeweils um eine Milliarde Menschen
zugenommen:
Jahr
ca. 1800
1927
1960
1974
1987
1999
Bevölkerung
1 Mrde
2 Mrde
3 Milliarden
4 Milliarden
5 Milliarden
6 Milliarden
Sprechen die Verdopplungszeiten (1 auf 2,2 auf 4, 3 auf 6 Milliarden) im Betrachtungszeitraum für ein exponentielles oder
überexponentielles Wachstum? Nach 1999 hat sich übrigens das Wachstum deutlich verlangsamt.
5.39 Angenommen, die Anzahl der Seerosen auf einem Teich verdoppelt sich jedes Jahr.
Am Ende des ersten Jahres befindet sich nur eine Seerose auf dem Teich; am Ende des 30. Jahres
ist der Teich vollständig mit Seerosen bedeckt. Wann ist a) die Hälfte, b) ein Viertel, c) ein
Achtel des Teichs bedeckt?
5.40 Eine Legende erzählt, dass sich der Erfinder des Schachspiels folgende Belohnung erbeten hat:
man möge auf das erste Feld ein Weizenkorn legen, auf das zweite zwei, auf das dritte vier
Weizenkörner usw.; jedes Mal möge also die Anzahl der Weizenkörner verdoppelt werden.
a) Wie lautet die rekursive Darstellung für die Anzahlen der
Weizenkörner auf den Feldern des Schachbrettes? Wie
[
lautet die Termdarstellung?
b) Welche Masse an Weizen würde dies für jeden der 6 Milliarden Bewohner der Erde ergeben,
wenn ein Weizenkorn eine Masse von etwa 0,05 g besitzt? & •"'
5.41 Ein Betrieb bietet einem Angestellten bei seiner Einstellung die Wahl zwischen zwei
Gehaltsvarianten:
Variante A: Monatliches Anfangsgehalt € 1.800,-, jährliche Erhöhung um € 55,-. Variante B:
Monatliches Anfangsgehalt wie bei A, jährliche Erhöhung um 3%.
a) Gib die Monatsgehälter für die ersten 6 Jahre an.
b) Welche Variante ist bei einer 15-jährigen Betriebszugehörigkeit günstiger, wenn als Kriterium
die Verdienstsumme in dieser Zeit herangezogen wird (12 Monatsgehälter pro Jahr)?
5.44 Im Jahre 2004 betrug die Weltbevölkerung etwa 6,4 Mrd. Menschen. Gleichzeitig betrug die
jährliche Wachstumsrate etwa 1,2%.
a) Nach wie vielen Jahren würde sich die Weltbevölkerung verdoppeln, wenn die jährliche
Wachstumsrate konstant bliebe?
b) Wie groß wäre die Weltbevölkerung im Jahre 2050, wenn die jährliche Wachstums-rate
gleich bliebe?
c) Nach der UN-Bevölkerungsprognose 2004 wird im Jahre 2050 die Weltbevölkerung 8,9
Mrd. Menschen betragen. Welcher mittleren jährlichen Wachstumsrate würde dies
entsprechen?