Professor Botan liest in einem Buch über

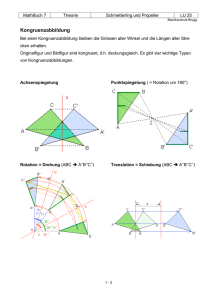
BLK – Sinus
Thema:
Zentrische Streckung
RS – Bad Bramstedt
H. Bernhardt
Aufgabe:
Professor Botan liest in einem Buch über Pflanzenfarbstoffe. Leider ist sein Augenlicht so
schlecht, dass er selbst bei groß geschriebenen Buchstaben noch eine Lupe benötigt.
Nimmt man den ersten Originalbuchstaben eines Pflanzenfarbstoffes, erscheint dieser nach
der Vergrößerung durch die Lupe wie unten abgebildet.
Vergrößerter Buchstabe
Originalbuchstabe
.
a) Finde heraus, wo bei der oberen Abbildung das Zentrum der Lupe liegt.
b) Ermittle die Lupenvergrößerung.
c) Erkennst du mathematische Beziehungen zwischen dem Originalbuchstaben und
dem vergrößerten Buchstaben?
d) Der vierte Buchstabe dieses Farbstoffes ist ein T.
Bilde diesen Buchstaben durch Streckung von Z aus mit dem Vergrößerungsfaktor k = 4
ab.
e) Der letzte Buchstabe (der 11.) ist ein L.
Hier ist die Lupenvergrößerung ( 4 - fach) dargestellt. Wie sah das Original aus?
e) Weißt du, wie der Pflanzenfarbstoff heißt?
Hier ist die an einer Geraden gespiegelte Lösung mit der dazu gehörenden
Spiegelgeraden:
Aufgabe 2
Färbe zunächst die Rechtecke wie angegeben ein.
Untersuche nachfolgende Fragen für
Fall I :Das gelbe Rechteck sei die Originalfigur.
a) Bestimme den Vergrößerungsfaktor der Seitenlängen von der Originalfigur
(gelbes Rechteck) zu den Seitenlängen des jeweilig anderen Rechtecks.
b) Finde jeweils einen Zusammenhang zwischen dem Flächeninhalt des gelben
Rechtecks und dem Flächeninhalt des vergrößerten Rechtecks.
c) konstruiere das Streckungszentrum Z zwischen der Originalfigur (gelbes Rechteck)
und der jeweiligen Bildfigur.
Fall II. : Das rosa Rechteck sei die Originalfigur.
a) Bestimme den Streckungsfaktor der Seitenlängen von der Originalfigur (rosa
Rechteck) zu den Seitenlängen einer kleineren Bildfigur.
b) Finde einen Zusammenhang zwischen dem Flächeninhalt der Originalfigur und dem
Flächeninhalt des jeweils verkleinerten Rechtecks.
BLK – Sinus Thema: Zentrische Streckung
RS – Bad Bramstedt
Lösungen soweit zeichnerisch mit dem PC möglich.
Aufgabe:
Professor Botan liest in einem Buch über Pflanzenfarbstoffe. Leider ist sein Augenlicht so
schlecht, dass er selbst bei groß geschriebenen Buchstaben noch eine Lupe benötigt.
Nimmt man den ersten Originalbuchstaben eines Pflanzenfarbstoffes, erscheint dieser nach
der Vergrößerung durch die Lupe wie unten abgebildet.
Vergrößerter Buchstabe
Originalbuchstabe
i
i
a) Finde heraus, wo bei der oberen Abbildung das Zentrum der Lupe liegt.
Siehe Abbildung.
b) Ermittle die Lupenvergrößerung.
ZA = 3,4 cm ZB = 3,4 cm
ZA i= 13,6 cm ZB i= 13,6 cm,
die Lupenvergrößerung liegt bei 4
c) Erkennst du mathematische Beziehungen zwischen Originalbuchstaben und dem
vergrößerten Buchstaben?
ZA i  4 * ZA ;
ZB i  4 * ZB
d) Der vierte Buchstabe dieses Farbstoffes ist ein T.
Bilde diesen Buchstaben durch Streckung von Z aus mit dem Vergrößerungsfaktor k = 6
ab.
Strecke ZP i = 6 * Strecke ZP
( P ist ein Punkt auf den Buchstaben T, Pi ist der zugehöriger Bildpunkt auf dem Bild.
Pi
P
Entsprechend bei L; k = 0,25
e) Weißt du, wie der Pflanzenfarbstoff heißt? Gespiegelte Lösung:
Name des Farbstoffes: XANTHOPHYLL
Aufgabe 2
Färbe zunächst die Rechtecke wie angegeben ein.
Untersuche nachfolgende Aspekte für:
Fall I
a) Bestimme den Vergrößerungsfaktor der Seitenlängen von der Originalfigur (gelbes
Rechteck) zu den Seitenlängen der anderen Rechtecke.
b) Finde jeweils einen Zusammenhang zwischen dem Flächeninhalt des gelben Rechtecks
und dem Flächeninhalt des vergrößerten Rechtecks.
Beispielhaft Fall I: Vergrößerungsfaktor
Originalfigur gelb
Bildfigurgrün
Seite a
8 mm
20 mm
Seite b
12mm
30 mm
Flächeninhalt
96 mm²
600 mm²
Vergrößerungsfaktor
k
2,5
2,5²
96  2,5²= 600cm²
Originalfigurgelb
Bildfigurblau
Seite a
8 mm
10 mm
Seite b
12 mm
15 mm
Flächeninhalt
96 mm ²
Originalfigurgelb
150 mm²
1,25²
96  1,25²= 150 mm²
Bildfigurrosa
Vergrößerungsfaktor
k
5
Seite a
8 mm
40 mm
Seite b
12 mm
60 mm
Flächeninhalt
96 mm²
Vergrößerungsfaktor
k
1,25
2400 mm²
5²
96  5²= 2400 cm²
c) Konstruiere das Streckungszentrum Z zwischen der Originalfigur (gelbes Rechteck)
und der jeweiligen Bildfigur.
Allgemein: ZA  K = ZA i
Fall II. : Das rosa Rechteck sei die Originalfigur.
a) Bestimme den Streckungsfaktor zwischen den Seitenlängen Originalfigur (rosa
Rechteck) und den Seitenlängen einer kleineren Bildfigur.
b) Finde einen Zusammenhang zwischen dem Flächeninhalt der Originalfigur und
dem Flächeninhalt des jeweils verkleinerten Rechtecks.
Beispielhaft Fall II: Streckungsfaktor
Seite a
Originalfigurrosa
40 mm
Seite b
Flächeninhalt
Bildfigurblau
10 mm
60 mm
15 mm
2400 mm²
150 mm²
Streckungsfaktor k
0,25
=
1
4
0,25²
2400  0,25² =
150 mm²
Allgemein: Ai = A  k²