Kapitel_4_3_3

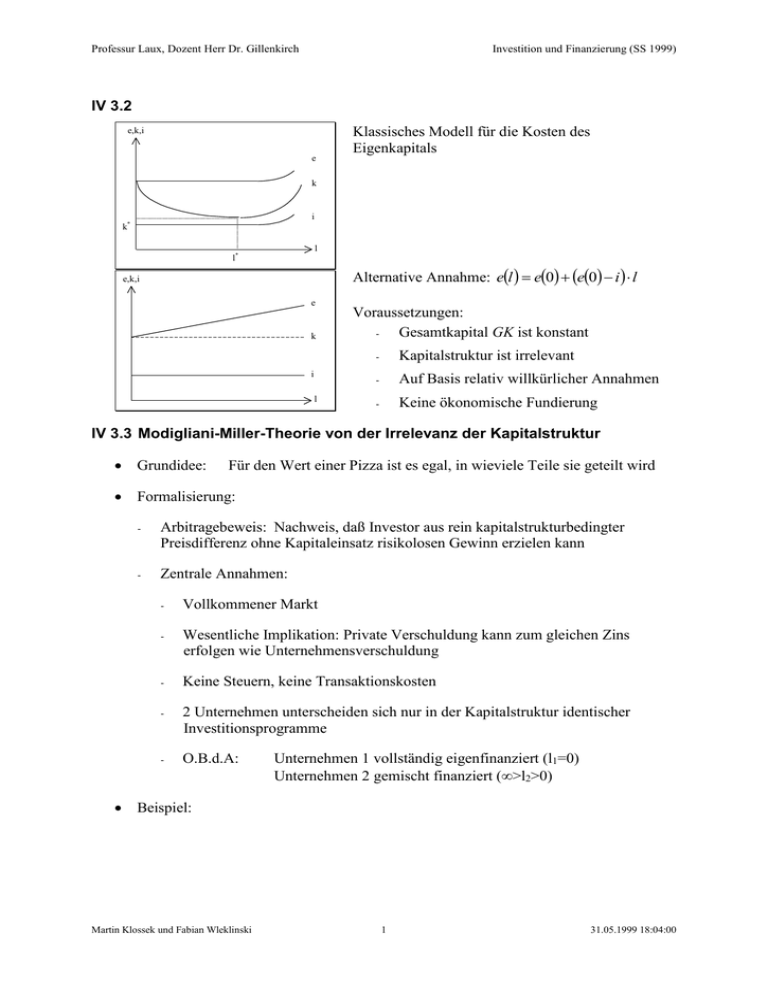
Professur Laux, Dozent Herr Dr. Gillenkirch
Investition und Finanzierung (SS 1999)
IV 3.2
e,k,i
e
Klassisches Modell für die Kosten des
Eigenkapitals
k
i
k*
l
l*
Alternative Annahme: el   e0  e0  i   l
e,k,i
e
k
i
l
Voraussetzungen:
Gesamtkapital GK ist konstant
-
Kapitalstruktur ist irrelevant
-
Auf Basis relativ willkürlicher Annahmen
-
Keine ökonomische Fundierung
IV 3.3 Modigliani-Miller-Theorie von der Irrelevanz der Kapitalstruktur
 Grundidee:
Für den Wert einer Pizza ist es egal, in wieviele Teile sie geteilt wird
 Formalisierung:
-
Arbitragebeweis: Nachweis, daß Investor aus rein kapitalstrukturbedingter
Preisdifferenz ohne Kapitaleinsatz risikolosen Gewinn erzielen kann
-
Zentrale Annahmen:
-
Vollkommener Markt
-
Wesentliche Implikation: Private Verschuldung kann zum gleichen Zins
erfolgen wie Unternehmensverschuldung
-
Keine Steuern, keine Transaktionskosten
-
2 Unternehmen unterscheiden sich nur in der Kapitalstruktur identischer
Investitionsprogramme
-
O.B.d.A:
Unternehmen 1 vollständig eigenfinanziert (l1=0)
Unternehmen 2 gemischt finanziert (>l2>0)
 Beispiel:
Martin Klossek und Fabian Wleklinski
1
31.05.1999 18:04:00
Professur Laux, Dozent Herr Dr. Gillenkirch
U1
1
Y
MW2 (EK)
MW(FK)
Gesamtwert
Y – ik
e
Investition und Finanzierung (SS 1999)
U2
200.000
1.000.000
0
1.000.000
200.000
20%
200.000
600.000
500.000
1.100.000
175.000
29,2%
Annahme: Aktionär besitzt 10% der Aktien von U2
-
Strategie: „Buy low, sell high“
-
Verkaufe 10% der Aktien von U2 und bekomme 60.000 GE
-
Als Aktionär Kapitalstrukturrisiko mit l 
-
500000
5

1100000 11
Kreditaufnahme: „homemade leverage“, Kredit 50.000 GE,
Gesamtbarbestand: 110.000 GE
-
Kaufe Aktien von U1 (11% des GK)
-
11% des Bruttogewinns als Ausschüttung = 22.000 GE
-
Position als Aktionär von U2: 0,1200000  0,05  500000  17500
-
Position als Aktionär von U1: 0,11200000  0,05  50000  19500
jährlicher, risikoloser Gewinn von 2000 GE
Markt kennt diesen Mechanismus
-
Erwartung steigender Nachfrage nach Aktien von U1
-
Steigender Preis
-
sinkende EK-Kosten
Anschlußfrage:
Auf welchem Wert müssen die EK-Kosten von U1 sinken, damit
keine Arbitrage möglich ist?
Annahme:
U2 ist korrekt bewertet  MW(EK1) muß auf 1.100.000 GE steigen
! 200000
e
 18,1890
1100000
 Variation des Beispiels:
MW(FK2)=400.000 GE
-
Gesamtwert U2=900.000 GE
-
umgekehrte Strategie für Aktionäre von U1, Anteil 10%
-
Verkauf der U1-Aktien für 100.000 GE
1
Y=Gewinn
MW=Marktwert
Martin Klossek und Fabian Wleklinski
2
2
31.05.1999 18:04:00
Professur Laux, Dozent Herr Dr. Gillenkirch
Investition und Finanzierung (SS 1999)
-
l2=4/9
-
Aufteilung der 100.000 GE auf Kapitaltitel in diesem Verhältnis:
/9100.000 in Aktien, 5/9100.000 in Obligation, damit Aktien-Anteil von
100.000 1
 am Bruttogewinn
900.000 9
4
-
Schlußfolgerung:
Bei gegebenem Investitionsprogramm sind die Kapitalkosten unabhängig von der
Kapitalstruktur l, d.h. k ist eine Konstante.
-
Vergleich traditionelle These mit Modigliani-Miller-Problem
-
Problem: Konstanz der WACC kann auf zwei Arten argumentativ untermauert
werden:
-
-
-
traditionelle These
-
Modigliani-Miller
Unterschied:
Argumentationsweg!
-
traditionelle These:
Verhaltensannahmen
-
Modigliani-Miller:
Arbitragbeweis
Schlußfolgerung aus Modigliani-Miller:
-
Kapitalkosten bei gegebenem Investitionsprogramm sind konstant. Welcher
Verlauf der EK-Kosten resultiert?
Angenommener Verlauf der FK-Kosten:
k l   el 
il   i , k l   k
EK
FK
 il 
EK  FK
EK  FK
bzw.
el   k l   k l   il  l  k  k  i l
-
EK-Kosten sind lineare Funktion von l. L=0, d.h. vollständige
Eigenfinnzierung e(0)=k und damit: el   e0  e0  i l
Martin Klossek und Fabian Wleklinski
3
31.05.1999 18:04:00