Physik 9_II - Ihre Homepage bei Arcor
Werbung
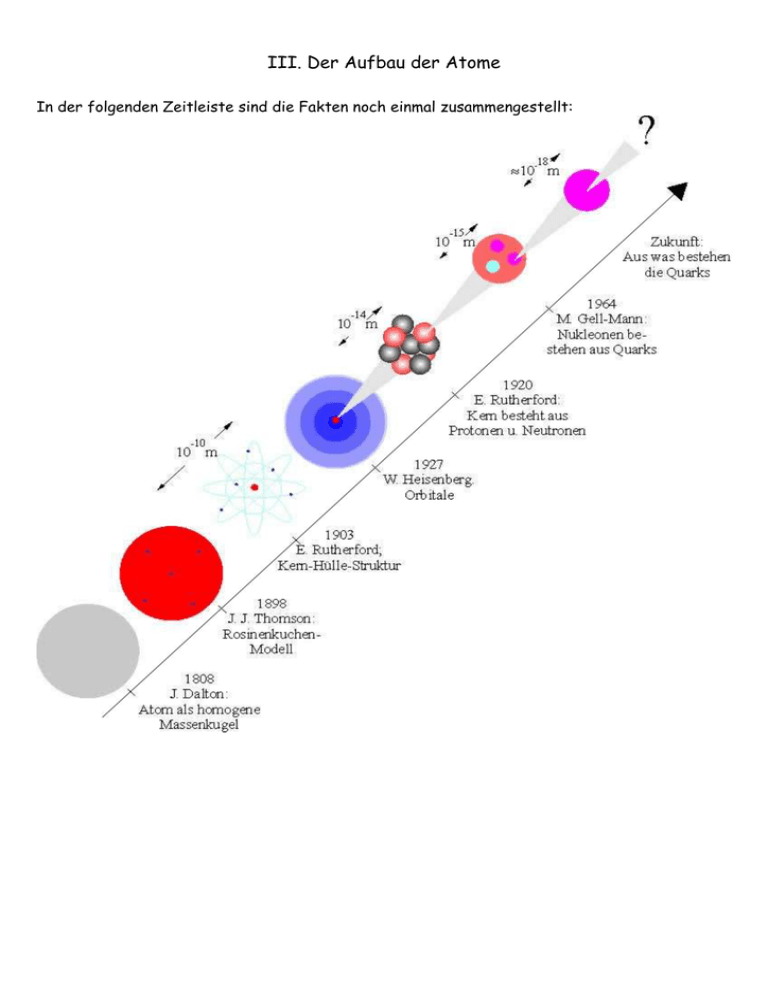
III. Der Aufbau der Atome In der folgenden Zeitleiste sind die Fakten noch einmal zusammengestellt: Veranschaulichung atomarer Größenordnungen: Vom Molekül zum Quark: Zur Bestimmung der Größe eines Atoms dient der Ölfleckversuch: Um das Grundprinzip des Versuchs besser verstehen zu können, betrachten wir zunächst nicht Moleküle sondern Erbsen. In einen Becher schütten wir gerade so viele Erbsen, dass sich eine einlagige Schicht bildet. Um die durchschnittliche Höhe dieser Erbsenschicht zu ermitteln könnte man den Durchmesser jeder einzelnen Erbse ausmessen (was uns messtechnisch möglich wäre) und dann einen Mittelwert errechnen (Methode 1). Man kann aber auch wie folgt vorgehen (Methode 2): - Man bestimmt zunächst den Radius des Bechers und errechnet hieraus die Fläche A der einlagigen Erbsenschicht. - Man füllt die Erbsen in einen Messzylinder und ermittelt so das Volumen V der Erbsen. - Die durchschnittliche Höhe der Erbsenschicht ergibt sich dann näherungsweise aus dem Quotienten V/A. Will man den Durchmesser eines Moleküls bestimmen, so ist für uns die Methode 1 nicht möglich. Wenn es jedoch gelingt eine einlagige Molekülschicht (monomolekulare Schicht) herzustellen, dann können wir nach Methode 2 vorgehen. Beim Ölfleckversuch lässt man einen einzigen Tropfen eines Ölsäure-Leichtbenzin-Gemisches mittels einer Tropfbürette auf eine ruhige ebene Wasseroberfläche auftropfen, die vorher mit Lykopodium (Bärlappsporen) bestreut war. Der Tropfen der Mischung breitet sich kreisförmig aus. Nach dem Verdampfen des Leichtbenzins verringert sich der Kreisdurchmesser auf den Wert d. Wenn man nun davon ausgeht, dass sich auf dem Wasser eine einmolekulare Schicht von Ölsäuremolekülen ausgebildet hat, kann man - ähnlich wie bei den Erbsen - den Durchmesser eines Moleküls abschätzen. Der Streuversuch von Rutherford Um über die Struktur eines Mikroobjekts (Atom, Kern, Proton, Neutron) Näheres zu erfahren, hat sich das sogenannte Streuexperiment hervorragend bewährt. Dabei wird das zu untersuchende Objekt mit Teilchen bombardiert und die Verteilung der gestreuten Teilchen beobachtet. Grundaufbau eines Streuexperiments Ein kollimierter Teilchenstrahl wird an einem Target (engl.: Ziel) gestreut. Aus der Winkelverteilung der gestreuten Teilchen schließt man auf die Struktur des Targets und auf die Art der Kräfte zwischen den Geschossen und den Bausteinen des Targets. Aus der Streuverteilung der Geschosse und mit einer sinnvollen Modellvorstellung können dann Aussagen über die Struktur des zu untersuchenden Objekts gemacht werden. Nuklide und Isotope Kernladungszahl und Massezahl Der Kern eines Atoms besteht aus den positiv geladenen Protonen und den ungeladenen Neutronen. Die Masse von Proton und Neutron ist ungefähr gleich. Ihre Masse ist jeweils etwa 1800-mal so groß wie die eines Elektrons der Hülle. Teilchen Masse Ladung -27 Proton 1,6727·10 kg ≈ u +1,6022·10-19As = +e Neutron 1,6750·10-27 kg ≈ u ---31 Elektron 9,109·10 kg -1,6022·10-19As = -e u: Atomare Masseneinheit (-unit); u = 1,6605·10-27 kg Durchmesser ca. 1·10-15 m ca. 1·10-15 m < 1·10-18 m Kernladungszahl Z: - Die Zahl der Protonen in einem Kern bestimmt die Kernladungszahl Z. - Beim neutralen Atom stimmt die Elektronenzahl in der Hülle mit der Kernladungszahl überein. - Die Struktur der Atomhülle (wesentlich bestimmt durch die Elektronenzahl) bestimmt das chemische Verhalten eines Atoms. - Weiß man die Kernladungszahl eines Atoms so liegt damit auch der Name des Elements fest und umgekehrt. - Die Kernladungszahl eines Elements kann in einer Periodentafel nachgeschlagen werden. Ein Periodentafel findest du z.B. bei Wikipedia unter der Adresse: http://de.wikipedia.org/wiki/Periodensystem Massezahl A: Die Summe aus Protonenzahl Z und Neutronenzahl N ergibt die Massezahl A. A=Z+N Will man die Masse eines Atoms ungefähr bestimmen, so muss man nur die Massezahl A mit der atomaren Masseneinheit u multiplizieren: matom ≈ A·u Isotope: Kerne mit gleicher Protonenzahl Z aber verschiedener Massezahl A (und damit verschiedener Neutronenzahl N) bezeichnet man als Isotope. Aufgrund der gleichartigen Hüllenstruktur (beim neutralen Atom gilt: Protonenzahl = Elektronenzahl) sind Isotope chemisch nicht zu unterscheiden. Elementschreibweise: Ein Element X mit der Kernladungszahl Z und der Massezahl A wird weltweit einheitlich in folgender Form geschrieben: Elementsymbol: Die N-Z-Karte (Nuklidkarte): Man sieht, dass bei Atomen mit nicht zu großer Massezahl A die Zahl der Neutronen N und der Protonen Z etwa gleich groß ist. Man erkennt dies auch daran, dass sich die Atome in der Karte längs der Winkelhalbierenden im N-Z-System anordnen. Die Karte zeigt alle stabilen Atome im N-Z-System als schwarze Punkte. Die Linie der stabilen Kern weicht bei größerem Z von der Winkelhalbierenden ab, die Neutronenzahl überwiegt die Protonenzahl (vgl. hierzu auch die entsprechende Musteraufgabe: In der nebenstehenden N-Z-Karte (N: Neutronenzahl; Z: Protonenzahl) sind die stabilen Atomkerne als schwarze Punkte dargestellt. Auf der Winkelhalbierenden des Diagramms gilt N = Z. a) Wo liegen in diesem Diagramm isotope Kerne? b) Versuche eine Begründung dafür zu geben, dass die "Linie der stabilen Kerne" bei größeren Protonenzahlen von der Winkelhalbierenden nach unten abweicht. Lösung: a) Isotope Kerne haben gleiche Protonenzahl. Isotope Kerne liegen also im N-Z-System auf einer parallelen zu N-Achse (vgl. Skizze). Auf der oberen (roten) Parallelen liegen isotope Kerne mit Z = 40 (Zirconium). Auf der unteren (roten) Parallelen liegen isotope Kerne mit Z = 20 (Calcium). b) Die Ursachen für das Abweichen der "Linie der stabilen Kerne" von der Winkelhalbierenden nach unten, sind die Kurzreichweitigkeit der Kernkraft und der Langreichweitigkeit der Coulombkraft: In größeren Kernen sitzen schon so viele Protonen, dass ein neu einzubauendes Proton die abstoßende Coulombkraft von allen diesen Kernprotonen "spürt". Überwiegt diese Coumlombkraft die anziehende Kernkraft der unmittelbaren Nachbarn, so kann das Proton nicht stabil in den Kern integriert werden.) Hinweis: Die Kernladungszahl Z wird häufig auch als Ordnungszahl bezeichnet. Der Name Ordnungszahl wird verständlich, wenn man weiß dass die Chemiker die verschiedenen Elemente nach ihrer Protonenzahl anordnen. Weitere Aufgaben S. 63, Nr. 2, 3, 5, 8, 11, 12, 13 IV. Aufnahme und Abgabe von Energie 1. Energie der Photonen – Prismenspektrum Wenn Photonen auf Materie treffen und absorbiert werden, können die verschiedensten Effekte eintreten. Hier einige Beispiele: - Beim Auftreffen auf Materie können die Photonen eine Erwärmung des Körpers hervorrufen (die Atome in dem Körper bewegen sich heftiger). - Treffen die Photonen auf Pflanzen, so kann dort die Photosynthese in Gang kommen. - Bestrahlt man eine Solarzelle mit Photonen so tritt an der Zelle eine elektrischen Spannung auf. - Treffen Photonen auf die Haut, so kann es zu Bräunungseffekten kommen. Bei der Beleuchtung von bestimmten Substanzen tritt das Phänomen der Lumineszenz auf, d.h. die bestrahlten Körper senden selbst Licht aus. Den zuletzt genannten Effekt der Lumineszenz kann man benutzen, um eine qualitative Aussage über den Zusammenhang zwischen der Farbe des Lichts und der Energie der zugehörigen Photonen zu erhalten. Versuch: Prismenspektrum und Zinksulfidschirm Man entwirft im abgedunkelten Raum mit einem Geradsichtprisma ein kontinuierliches Spektrum und hält in dieses Spektrum einen Zinksulfidschirm. Schaltet man die Lichtquelle ab, so leuchtet dieser Schirm in dem Bereich, wo das blaue Licht auftraf und rechts davon grünlich auf. Aus dem Versuchsergebnis kann man schließen, dass die Photonen des blauen und ultravioletten Lichts in der Lage sind auf dem Zink-Sulfid-Schirm Phosphoreszenz auszulösen. Die Photonen des roten, gelben und grünen Lichts dagegen nicht. Offensichtlich nimmt die Energie der Photonen vom roten zum blauen Bereich des Spektrums zu. Anstelle des Zink-Sulfid-Schirms kann man auch nur ein schmales phosphoreszierendes Leuchtband in das Spektrum halten. Dann ergibt sich etwa die folgende Situation: - Die Energie der Photonen hängt von der Farbe des entsprechenden Lichts ab. - Die Photonenenergie nimmt vom roten zum blauen Rand des Spektrums zu. Verschiedene Typen von Spektren: Emissionsspektren und Absorptionsspektren Unter dem Emissionsspektrum versteht man das elektromagnetische Spektrum, das von Körpern, Atomen oder Molekülen nach geeigneter Anregung (Erhitzung, Stoß durch Elektronen usw.) ausgesandt wird. Die Körper, Atome oder Moleküle stellen hierbei die Strahlungssender dar. Heiße Materialien (z.B. eine Glühwendel oder die Sonne) senden in der Regel ein kontinuierliches Spektrum aus, während Atome oder Moleküle eines verdünnten Gases sogenannte Linienspektren emittieren, die charakteristisch für das jeweilige Atom bzw. Molekül sind. Durchstrahlt man mit weißem Licht (nicht zu heiße) Körper, Atome oder Moleküle so kann es sein dass im an sich kontinuierlichen Spektrum des weißen Lichts nach der Durchstrahlung Linien oder ganze Bereiche fehlen. In diesem Fall spricht man von einem Absorptionsspektrum. Die Körper, Atome oder Moleküle stellen in diesem Fall Strahlungsabsorber dar. Kontinuierliches Emissionsapektrum: diskretes Emissionsspektrum: diskretes Absorptionsspektrum: Zusammenfassung: Aufgaben S. 74 Nr. 1 Energiestufen im Atom Die Emissionsspektren von verdünnten Gasen sind in der Regel Linienspektren. Im Photonenbild bedeutet dies, dass die Gasatome Photonen mit ganz bestimmten (diskreten) Energien aussenden. Dies lässt den Schluss zu, dass die Atome nur Zustände mit ganz bestimmten Energiebeträgen einnehmen. Beispiel: Angeregte Wasserstoffatome senden u.a. rotes Licht aus. Die entsprechenden Photonen haben die Energie von Eph,rot = 1,9 eV. Der Energiesatz führt uns zur Annahme, dass das Wasserstoffatom bei der Emission dieser Photonen von einem angeregten Zustand (Energie E2) in einen energieärmeren Zustand (Energie E1) übergeht, der energetisch exakt 1,9 eV unter dem angeregten Zustand liegt. Die Energieverhältnisse im Atom lassen sich durch ein sogenanntes Energie-Termschema übersichtlich darstellen. Ein Beispiel für ein mechanisches System, das drei Energiestufen einnehmen kann ist zum Beispiel ein auf dem Boden liegender Quader, wie die hier fotografierte Zündholzschachtel. niedrigster Energiezustand (Grundzustand) erster Anregungszustand * Aus den Anregungszuständen kann die Schachtel umfallen und dabei Energie abgeben (man kann das Umfallen hören). * Aus dem ersten Anregungszustand kann es in den Grundzustand umfallen, aus dem zweiten Anregungszustand kann es in den ersten Anregungszustand oder den Grundzustand umfallen. * Zum Wiederaufrichten braucht man immer eine bestimmte Energie von außen. zweiter Anregungszustand Deutung des diskreten Emissionsspektrums eines Atoms: Angeregte Atome senden ein diskretes Linienspektrum aus. Dies lässt sich mit der Annahme diskreter Energieniveaus im Atom verstehen. Beim Übergang von einem energetisch höheren (Energie E3) zu einem energetisch niedrigerem Niveau (Energie E2) wird ein Photon erzeugt, das Differenzenergie Ephoton = E3 - E2 besitzt und das Atom verlässt. Hinweise: * Da die sich die betrachteten Energieübergänge in der Atomhülle abspielen, kann man sich vorstellen dass bei der Lichtemission ein Elektron von einem energetisch höheren Niveau auf ein energetisch niedrigeres Niveau wechselt. * Man darf den Wechsel im Niveauschema auf keinen Fall als Ortswechsel auffassen: Es ist keineswegs so, dass z.B. beim Übergang von Niveau 3 auf das Niveau 2 ein Elektron von einer Bahn die weiter vom Kern entfernt ist auf eine kernnähere Elektronenbahn wechselt (wir werden später noch sehen, dass die Vorstellung von definierten Elektronenbahnen beim Atom sowieso nicht zulässig ist). Bei dem Übergang handelt es sich um einen "energetischen Abstieg". * In der Regel verharrt ein Atom nur eine extrem kurze Zeit (≈ 10-8 s) im angeregten Zustand. * Die Anregung eines Atoms kann z.B. durch die Absorption eines Photons, durch den Stoß mit einem Nachbaratom oder durch Stöße mit Elektronen erfolgen. * Wenn die lichtaussendenden Atome von ihren Nachbaratomen stark gestört werden (dies ist z.B. bei hohem Druck in einem Gas oder bei Flüssigkeiten und Festkörpern der Fall), dann senden diese Atome kein Linienspektrum, sondern ein kontinuierliches Spektrum aus. Deutung des diskreten Absorptionsspektrums eines Atoms: Befindet sich das oben betrachtete Atom im Grundzustand, so kann es z.B. durch ein Photon mit der Energie Ephoton = E3 - E1 oder durch ein Photon mit der Energie E*photon = E2 - E1 angeregt werden, da die Photonenenergie genau einer Energiestufe im Atom entspricht, die vom Grundzustand (in dem befindet sich das Atom zu Beginn der Betrachtung) aus erreichbar ist. Bei dem Anregungsprozess wird das Photon vernichtet, es fehlt im Licht, welches die Atome durchstrahlt. Die Energie des Photons steckt nun im Atom, das nach kurzer Zeit unter Photonenemission wieder in den Grundzustand übergeht. Photonen deren Energien nicht dazu führen, dass das Atom vom Grundzustand in einen möglichen höheren Energiezustand übergeht, werden vom Atom nicht absorbiert. Hinweise: * Beträgt die Energiestufe in einem Atom z.B. 1,9 eV und bestrahlt man das Atom mit Photonen der Energie 2,4 eV, so könnte man sich folgenden Prozess vorstellen: Die eingestrahlten Photonen geben 1,9 eV an das Atom zur Anregung ab und die restliche Energie von 2,4 eV - 1,9 eV = 0,5 eV bleibt in energieärmeren Photonen, welche die Atomschicht durchdringen. Versuche zeigen jedoch, dass dieser Prozess nicht stattfindet. Die 2,4eVPhotonen durchdringen die Atomschicht ohne Anregung. * Die obigen mechanischen Bilder können die Vorgänge im Atom nur teilweise illustrieren. Der Energieträger "Kugel" existiert auch noch nachdem er seine Energie abgegeben hat. Dagegen existiert ein Photon, das seine Energie an das Atom abgegeben hat, nicht mehr, es wird vernichtet. Aufgaben S. 74 Nr. 2, 3, 4, 5, 6, 7, 8 Entstehung der Röntgenstrahlung Geschichte: Wilhelm Conrad Röntgen, einer der größten Physiker, den es je gab, wurde am 27.3.1845 in Lennep im Bergischen Land (Rheinland) geboren. Kurz danach zog er mit seiner Familie nach Apeldoorn in den Niederlanden. Dort verlebte er von 1848 bis 1862 seine Kindheit bzw. Jugend. Im Jahre1862 folgte der Umzug seiner Familie nach Utrecht, wo er die Technische Schule besuchte. Doch man halte sich fest: 1864 flog er ohne gültigen Abschluß von der Schule!!!! Er, das Genie!? Einfach unfassbar. Doch muß dazu gesagt werden, daß der Grund ein ehrenwerter war! Gerüchten zufolge jedenfalls. Nachdem seine Klasse einem Lehrer einen Streich gespielt hatte, war dieser außer sich vor Wut und wollte sich gar nicht mehr einkriegen. Da sich aber keiner schuldig bekannte, tat dies Röntgen, um dem Theater ein Ende zu bereiten. Er wird sich später wohl auch gefragt haben, ob es das wert war. In Deutschland und den Niederlanden wurde er nämlich 1864 zunächst mangels eines Schulabschlusses nicht von Universitäten angenommen und musste so erst einmal ein weniger spannendes Dasein als Gasthörer führen. Woran arbeitete Röntgen? In der zweiten Hälfte des 19. Jahrhunderts untersuchte man verstärkt den Transport elektrischer Ladungen in Gasen. Man benutzte dafür sogenannte Entladungsröhren, in denen ein Vakuum herrschte (so gut es halt ging) und die folgendermaßen aufgebaut waren. Die Kathode bestand aus einem heißen Glühdraht, welcher Elektronen produzierte. Zwischen Kathode und Anode wird eine sehr hohe Spannung angelegt, welche die Elektronen stark beschleunigt. Dazu muss man wissen, dass man damals in der Physik die Elektronen noch nicht kannte. Alles, was man sah, war, dass zwischen den beiden Elektroden ein schmaler Streifen glühte. Es war nicht klar, ob dies Teilchen oder Wellen waren. Man nannte diese Art von Strahlung "Kathodenstrahlen". Röntgen, der eigentlich auf einem ganz anderen Gebiet arbeitete, wollte die gemachten Experimente selber noch mal durchführen. Vielleicht wunderte es ihn, dass sich Fotoplatten neben der Entladungsröhre leicht schwärzten und er untersuchte dies. Man führte damals die Schwärzung auf UV-Licht zurück - aber Röntgen glaubte wohl nicht an diese Vorstellung. Es gibt sonst nämlich auch keinen offensichtlichen Grund, weshalb Röntgen den folgenden, entscheidenden Versuch gemacht haben sollte. Der Versuch: Also, egal ob er eine unsichtbare Strahlung vermutete oder nicht, er nahm eine einfache Änderung am bekannten Versuchsaufbau vor. Er benutzte immer noch die gleiche Röhre, die er mit einer Vakuumpumpe so luftleer wie damals möglich machte. Die Spannung, die zur Beschleunigung der Elektronen benötigt wurde, erzeugte er mit einem Funkeninduktor. Er bedeckte die Röhre nun aber völlig mit schwarzer Pappe, so daß weder normales noch UV-Licht durchkommen konnte. Als plötzlich der Schirm aus fluoreszierendem Material aufleuchtete, war Röntgen sofort klar, dass es eine neue Art von unsichtbaren Strahlen gab, die durch Materie (Stoffe) durchging. Es ist nicht überliefert, was Röntgen in diesem Augenblick gedacht hat, ob er sich der historischen Bedeutung bewusst war auf jeden Fall muss es unglaublich spannend und aufregend gewesen sein! Dadurch, dass er die Röhre mit schwarzer Pappe abgedeckt hatte, konnte normales (für das menschliche Auge sichtbares) Licht nicht hinausdringen. Da nun trotzdem ein Schirm im Raum aufblitzte, folgerte Röntgen richtig, dass es eine unbekannte, unsichtbare Art von Strahlen geben musste. Doch hatte er ja noch keinen blassen Schimmer, wieso und wo diese Strahlen überhaupt entstanden!! Diesen Fragen ging er in den nächsten 6 Wochen mit unbeschreiblicher Gewissenhaftigkeit nach, ohne irgend jemandem davon zu erzählen. Seiner Frau sagte er nur: "Die anderen würden denken, ich bin total durchgedreht!" Sogar sein Bett verlegte er in sein Labor!!! Seine Gründlichkeit ging so weit, dass er in diesen 6 Wochen so viel über diese neuen "XStrahlen" (so nannte er sie) herausfand, dass in dem folgenden Jahrzehnt, trotz massiven Aufwandes vieler Physiker, kaum neue Erkenntnisse erzielt werden konnten. Was sind Röntgenstrahlen? Röntgenstrahlen werden generell immer dann erzeugt, wenn Elektronen bzw. ein Kathodenstrahl auf Material trifft. Es gibt jedoch zwei verschiedene Möglichkeiten, wie bei diesem Aufprall Röntgenstrahlen entstehen können. Deswegen unterscheidet man zwischen charakteristischer Strahlung und Bremsstrahlung. Charakteristische Strahlung: Die Erzeugung charakteristischer Röntgenstrahlung beginnt damit, dass Elektronen, die auf ein Material geschossen werden, Elektronen aus den Bahnen der Atome herausschießen. Wenn nun ein Elektron aus seiner Bahn rausgeschossen worden ist, hinterlässt es dort ein "Loch". Dieses wird nun dadurch gefüllt, dass ein Elektron aus einer äußeren Schale in das Loch hineinspringt. Dabei wird Energie frei, welche sich in Form von Licht, nämlich Röntgenlicht, äußert. Dieses Licht, das immer dann auftritt, wenn ein Elektron von einer äußeren in eine innere Bahn springt, wird charakteristische Röntgenstrahlung genannt. Wichtig ist bei dem ganzen eben beschriebenen Vorgang, dass die heranfliegenden Elektronen nur Elektronen mit gleicher oder niedrigerer Bindungsenergie herausschießen können. Auch ist das Licht, das beim Nachfüllen eines Elektrons der inneren Schale erzeugt wird, energiereicher als wenn ein Loch auf einer der äußeren Schalen gefüllt wird. Es gibt also immer anderes Licht (in der Wellenlänge verschieden), abhängig davon, aus welcher Schale ein Elektron rausflog und aus welcher Schale das nachfüllende kam. Anhand dieser Strahlung kann der Physiker auf das Material zurückschließen, auf das geschossen wurde. Das liegt daran, dass jeder Stoff anders angeordnete Schalen bzw. Energieniveaus hat und damit ein für ihn typisches Spektrum charakteristischer Röntgenstrahlung aufweist. Bremsstrahlung: Das Material, auf das die Elektronen treffen, besteht aus einem Atomgitter (klicke hier, wenn Du vergessen hast, wie ein Atom mit Kern und Hülle etc. aussieht). Das Verhalten der Elektronen in Materie könnte man mit dem eines Skiläufers vergleichen. Der Skiläufer erkennt das/die Hindernis/se rechtzeitig und fährt um sie rum. Übertragen heißt das: das negative Elektron fliegt nah an einem Atomkern (positiv) vorbei und erfährt eine gewisse Anziehungskraft, da sich ungleichnamige Ladungen ja anziehen. Diese Kraft reicht jedoch nur dazu aus, die Flugbahn des Elektrons zu krümmen. In jeder Kurve wirbelt unser Skiläufer ein bisschen Schnee auf, d.h., seine Energie nimmt langsam ab (er wird abgebremst). Diese Energie geht in den Schnee über, der in jeder Kurve aufgewirbelt wird. Im Falle des Elektrons, das beim Vorbeifliegen an einem Atomkern ebenfalls abgebremst wird (Krümmung der Flugbahn), wird die dabei frei werdende Energie in kleinen Portionen von Röntgenlicht abgestrahlt. Eigenschaften der Röntgenstrahlung: - Röntgenstrahlen durchdringen Materie, d.h., sie werden nur selten von den Atomen absorbiert. - Röntgenstrahlen sind unsichtbar für das menschliche Auge, da sie zu kurzwellig sind (nicht mehr in dem von uns sehbaren Spektrum). - Röntgenstrahlen ionisieren Luft und Gase. - Röntgenstrahlen sind weder durch elektrische noch magnetische Felder ablenkbar. Reaktionen in der Gesellschaft: In der Gesellschaft wurde diese naturwissenschaftliche Entdeckung wie keine vor ihr aufgenommen. Das Gefühl, etwas sehen zu können, was bisher absolut verborgen war, nämlich das Innere des eigenen Körpers, löste viele Emotionen aus. Normalerweise werden physikalische Entdeckungen nur in einem kleinen Kreis Interessierter diskutiert, aber diesmal war jeder verrückt nach Einzelheiten, weil es sie selber betraf. Das Interesse der Bevölkerung ging bald so weit, dass selbst auf Partys Röntgenapparate als Attraktion aufgestellt wurden. Zum Vergnügen wurden dann den ganzen Abend lang Fotos von den eigenen Händen oder anderen Körperteilen gemacht und anschließend ausgiebig bestaunt. Von Strahlenschutz hatte man damals offenbar keinen blassen Schimmer. Es ging soweit, dass jeder Firlefanz geröntgt wurde. Röntgenstrahlung war plötzlich Bestandteil der Öffentlichkeit und es wurden sogar etwas ironische Karikaturen wie die obige (Abendgesellschaft der damaligen Zeit) in Zeitungen veröffentlicht. Selbst in Schuhgeschäften fand die neue Entdeckung Anwendung - der Kunde konnte sich die Position seiner Füße in den neuen Schuhen angucken! Als Röntgen am 23.1. 1896 in Würzburg seinen einzigen öffentlichen Vortrag hielt, wurde er mehrmals von stehenden Ovationen unterbrochen. Nachdem er dann während seines Vortrags auch noch die Hand des Leiters der medizinischen Fakultät, Prof. von Kölliker, mit Röntgenstrahlen fotografierte, kannte der Beifall keine Grenzen mehr. Auf den spontanen Vorschlag von Kölliker hin wurden die "X-Strahlen" ab dann in Deutschland nur noch Röntgenstrahlen genannt. Am deutlichsten wird diese Welle der Begeisterung durch die Tatsache, dass selbst der Kaiser, der sonst mit Physik nichts am Hut hatte, Röntgen schon 2 Wochen nach seiner Entdeckung zu sich einlud, um ihn zu ehren. Viel wichtiger war dem Kaiser aber wohl eine sofortige persönliche Vorführung der Strahlen. Aufgaben S. 74 Nr. 9, 10 Strahlung radioaktiver Nuklide Entdeckung der natürlichen Strahlung durch Becquerel: Henri Becquerel entstammt einer Wissenschaftlerfamilie (schon sein Großvater und sein Vater waren Physik-Professoren). Seine Entdeckung der radioaktiven Strahlung war einem glücklichen Umstand zu verdanken. * Becquerel beschäftigte sich zunächst mit optischen Phänomenen. * Zusammen mit seinem Vater untersuchte er die Phosphoreszenzspektren erhitzter Minerale sowie die Phosphoreszenz von Uransalzen. Mit der Entdeckung der Röntgenstrahlen (Conrad Röntgen 1895) wurde das Interesse der Physiker verstärkt auf ein Phänomen gelenkt, das anscheinend eng mit dieser Strahlung zusammenhing: Viele von Röntgenstrahlung getroffene Körper fluoreszieren. So leuchtete z.B. die Glaswand einer in Betrieb befindlichen Röntgenröhre in einem fahlen Licht auf. Aus dieser Beobachtung entstand die Vermutung, dass die Fluoreszenz und die Emission der Röntgenstrahlen in einem Zusammenhang stehen. Becquerel verwendete als fluoreszierendes Material eine Uranverbindung. Zur Untersuchung legte er eine Probe davon auf eine lichtdicht verpackte Fotoplatte und bestrahlte die Probe zur Fluoreszenzanregung mit Sonnenlicht. Tatsächlich zeigte die Platte nach der Entwicklung die Umrisse des fluoreszierenden Körpers. Wenige Tage nach diesem Versuch trat ein entscheidender Zufall ein. Da mehrere Tage keine Sonne schien blieb ein Uranpräparat auf einer Fotoplatte in einer Schublade liegen. Bei der Entwicklung dieser Platte stellte Becquerel zu seiner Überraschung fest, dass die Platte trotzdem intensiv geschwärzt war. Becquerel berichtet über seine Beobachtungen: "Es kann leicht gezeigt werden, dass die Strahlung des Uran-Kalium-Doppelsulfats (Kristallplättchen) emittiert wird, wenn es dem Sonnenlicht oder diffusem Licht ausgesetzt ist, nicht nur einige Lagen schwarzes Papier, sondern auch Metalle durchdringt, z.B. eine Platte oder dünne Schicht Aluminium. Ich möchte aber folgende Tatsache betonen, der ich große Bedeutung beimesse und die gänzlich außerhalb des Kreises jener Erscheinungen liegt, deren Beobachtung zu erwarten ist. Die selben Kristallplättchen, unter den selben Versuchsbedingungen auf die photographische Platte gelegt, abgeschirmt, aber selber von der Einwirkung äußerer Strahlung geschützt, also in völliger Dunkelheit gehalten, ergeben genau die selben Wirkungen auf der photographischen Platte. Becquerel fand später noch, dass die entdeckte Strahlung Gase ionisieren, also leitend machen und damit auch ein Elektroskop entladen kann. Im Jahre 1903 bekam er zusammen mit dem Ehepaar Curie den Nobelpreis für seine Entdeckung. Zu Ehren Becquerels verwendet man für die Einheit der Aktivität einer radioaktiven Probe das Becquerel (1 Bq = 1 s-1) Strahlungsarten: - Strahlung: Beim Alpha-Zerfall spucken große Atomkerne kleinere Atomkerne aus - nämlich die des Elements Helium: Diese so genannten Alpha-Teilchen bestehen aus jeweils zwei positiv geladenen Protonen und zwei neutralen Neutronen. Ein Beispiel für einen Alpha-Strahler ist Radium-226. Es zerfällt in Radon-222. Die Alpha-Teilchen haben eine ziemlich große Geschwindigkeit: Zwischen 15.000 bis 20.000 Kilometer pro Sekunde! Allerdings besitzt die Strahlung nur eine geringe Reichweite und lässt sich schon durch ein Blatt Papier oder eine dünne Alu-Folie abschirmen. Trotzdem gilt sie als ausgesprochen gesundheitsschädlich. Alphastrahlung steht zum Beispiel im Verdacht, bei Rauchern für die Entstehung von Lungenkrebs mitverantwortlich zu sein. Sie ist aber auch nützlich: Im täglichen Leben werden schwache Alpha-Strahler zum Beispiel in Rauchmeldern eingesetzt. * α-Teilchen können ein dickeres Blatt Papier bereits vollständig absorbiert werden. * Die Reichweite der α-Teilchen in Luft beträgt nur wenige Zentimeter. * α-Teilchen können durch starke Magnetfelder aufgrund ihrer positiven Ladung abgelenkt werden. - Strahlung: Beim Beta-Zerfall werden in der Regel negativ geladene Elektronen aus dem Kern geschleudert. Man spricht dann vom Beta-Minus-Zerfall. (Es gibt auch einen Beta-Plus-Zerfall, doch der ist unter den natürlichen Radionukliden viel seltener.) Die Elektronen, die die Strahlung ausmachen, kommen übrigens nicht aus dem Nichts: Sie entstehen dadurch, dass sich im Atomkern ein Neutron in ein Proton und ein Elektron umwandelt: Zerfall eines Neutrons im Atomkern Das Proton bleibt im Kern, das Elektron wird weggeschleudert. Das ist zum Beispiel beim Cäsium-137 der Fall. Es entsteht Barium-137. Die Reichweite von Beta-Strahlung kann in Luft mehrere Meter betragen, abschirmen lässt sie sich durch Aluminium- oder Kunststoffplatten von einigen Millimetern Dicke. Die Geschwindigkeit der Teilchen kann dabei von nahezu null bis zu Lichtgeschwindigkeit betragen. Im täglichen Leben trifft man Beta-Strahler als strahlentherapeutische Maßnahme: Krebsgeschwüre unter der Hautoberfläche können so bestrahlt werden. Bei der C14-Methode spielt die Beta-Strahlung ebenfalls eine Rolle: Sie misst die C14-Reste, die über die Jahrtausende beim Zerfall übrigbleiben. Mit ihnen kann man das Alter von archäologischen Fundstücken bestimmen. * β-Teilchen können durch Aluminium von wenigen Millimetern Wandstärke bereits vollständig absorbiert werden. * Die Reichweite der β-Teilchen in Luft beträgt wenige Meter. * ß-Teilchen können bereits durch schwächere Magnetfelder aufgrund ihrer negativen Ladung abgelenkt werden. Beim Beta-Plus-Zerfall werden Positronen - so zusagen „positive Elektronen” - aus dem Kern geschleudert. Bei der Beta-Plus-Strahlung wird im Kern aus einem Proton ein Neutron sowie ein Positron: Beta-Plus-Strahlung Natrium-22 ist ein solcher Beta-Plus-Strahler. - Strahlung: Gamma-Strahlung kann als elektromagnetische Welle bezeichnet werden und gleicht daher vom Wesen her der Röntgenstrahlung und dem sichtbaren Licht. Wesentlicher Unterschied: Röntgenstrahlung hat ihren Ursprung in der Atomhülle, Gammastrahlung im Kern. Gamma-Strahlung tritt oft auf, wenn beim Alpha- oder Beta-Zerfall überschüssige Energie in Form von Strahlung abgegeben werden muss. Sehr oft entsteht sie, wenn ein Atomkern aus einem energiereichen in einen energieärmeren Zustand zurückfällt, zum Beispiel beim Barium137m. Gammastrahlung tritt in Kernkraftwerken sowohl unmittelbar bei der Spaltung, als auch durch Energieabgabe der bei der Spaltung entstandenen Spaltprodukte auf. Genau wie Licht breitet sich Gamma-Strahlung mit Lichtgeschwindigkeit aus. Sie hat eine viel höhere Reichweite als Alpha- oder Beta-Strahlung: Um sie abzuschirmen, braucht man abhängig von ihrer Energie - Bleischilde mit einer Dicke von mindestens 20 Zentimetern oder Betonwände von mindestens einem Meter Dicke. Gammastrahlung wird zum Beispiel in der Krebstherapie eingesetzt. In vielen Ländern benutzt man sie außerdem, um Lebensmittel haltbar zu machen. * Die Reichweite der γ-Strahlung in Luft beträgt viele Meter. * γ-Strahlung wird nur durch dicke Bleiplatten oder sehr dicke Betonschichten absorbiert. * γ-Strahlung kann auch durch stärkste Magnetfelder nicht abgelenkt werden. * Das Verhalten der γ-Strahlung ist dem der Röntgenstrahlung sehr ähnlich. Gute Grafiken Buch S. 79 Aufgaben S. 90 Nr. 1, 2, 3, 6, Eigenschaften der natürlichen radioaktiven Strahlung: Nuklidkarte In der Nuklidkarte sind alle Nuklide mit ihren mit ihren Zerfallsarten, Halbwertzeiten, Zerfallsenergien u.ä. dargestellt. Die Kernladungszahl Z ist senkrecht und die Neutronenzahl N waagerecht aufgetragen. Isotope des selben Elements liegen auf einer waagerechten, Isotone auf einer senkrechten und Isobare auf einer schrägen Geraden. Die Farbe gibt die Zerfallsart des Kerns an. Die stabilen Kerne sind schwarz und liegen auf der Linie der Stabilität, die für kleine Nuklidzahlen mit der Winkelhalbierenden des I. Quadranten etwa übereinstimmt, also N = Z. Für größere Nuklidanzahl biegt sie nach unten ab, dort gilt N > Z. Beim Alphazerfall sinkt die Protonenzahl um 2 und sinkt die Neutronenzahl um 2. Beim Beta-Minus-Zerfall steigt die Protonenzahl um 1 und sinkt die Neutronenzahl um 1. Beim Beta-Plus-Zerfall sinkt die Protonenzahl um 1 und steigt die Neutronenzahl um 1. Nachweis radioaktiver Stahlung: Das Geiger-Müller-Zählrohr: Das Geiger-Müller-Zählrohr ist ein ziemlich einfaches Instrument - aber sehr wirkungsvoll zum Messen der Aktivität. Es besteht aus einem Metallrohr, vorne und hinten verschlossen, in dessen Inneren sich ein dünner Draht aus Wolfram befindet. Das Röhrchen enthält außerdem Gas (zum Beispiel Luft) unter niedrigem Druck und etwas Alkoholdampf. Die Halbwertszeit und das Zerfallsgesetz: Das Zerfallsgesetz für radioaktive Atome lautet - ganz analog zum Zerfallsgesetz beim Bierschaum: Weil man meistens die Menge der noch vorhandenen radioaktiven Atome mit der Ausgangsanzahl von Atomen ins Verhältnis setzt, findet man in Formelsammlungen in der Regel folgende - gleichbedeutende - Formel: Mit Hilfe dieser Formel lässt sich jetzt schon einiges über den Zerfall radioaktiver Stoffe vorhersagen. Welchen der folgenden Aussagen kann man wohl zustimmen? (Mehrere Antworten sind hier möglich.) a) Am Anfang zerfallen extrem viele Atome, im Laufe der Zeit werden es immer weniger. b) Wenn man lange genug wartet, ist kein Atom mehr da, das zerfallen könnte. c) Das Verhältnis von ursprünglich vorhandenen und derzeit noch vorhandenen Atomen ist konstant. d) Die radioaktiven Atome nehmen exponentiell zu. e) α ist eine Konstante, die bestimmt, wie schnell die Atome zerfallen. Wie lange dauert es, bis radioaktive Atome zerfallen? Für ein einzelnes, ausgewähltes Atom kann man nicht sagen, ob es in der nächsten Millisekunde zerfallen wird oder noch eine Woche oder gar ein Jahrhundert „lebt”. Für eine große Anzahl von Atomen kann man dagegen mit Hilfe des Zerfallsgesetzes sehr wohl statistische Aussagen machen. Die Halbwertszeit: Wie schnell die Atome im Mittel zerfallen, gibt die Konstante α an. Sie ist typisch für jedes Isotop; in ihr verbirgt sich die Halbwertszeit, mit deren Hilfe man auch das Zerfallsgesetz nochmal etwas anders formulieren kann: Die Zeit, in der die Hälfte der Kerne in einer Menge von Radionukliden zerfällt. Die Halbwertszeiten bei den verschiedenen Radionukliden sind sehr unterschiedlich, z. B. von 7,2 · 1024 Jahren bei Tellur-128 bis herab zu 2 · 10-16 Sekunden bei Beryllium-8. Beispiele für Halbwertszeiten auf S. 81 im Buch Die C14- Methode: Wie alt ist eigentlich der Neandertaler? Bei der Suche nach Antworten auf solche Fragen macht man sich die Tatsache zunutze, dass instabile Elemente mit einer bestimmten statistischen Wahrscheinlichkeit zerfallen. Die Altersbestimmung geht so: Lebende Organismen, also Menschen, Tiere oder Pflanzen, enthalten einen bestimmten Anteil des instabilen Kohlenstoff-14 (C14), der immer wieder neu aus der Umwelt aufgenommen wird. Nach dem Tod oder dem Absterben kann kein neuer Kohlenstoff-14 mehr aufgenommen werden, und der vorhandene Anteil zerfällt (Beta-MinusZerfall) zu Stickstoff-14. Allerdings ziemlich langsam: Man weiß, dass nach 5.730 Jahren genau die Hälfte der ursprünglich vorhandenen C14-Atome noch vorhanden sind. Wollen Wissenschaftler also bei einer Probe herausfinden, wie alt sie ist, dann reicht es aus, zu bestimmen, welcher Anteil des C14 in ihr noch nicht zerfallen ist. Das Alter lässt sich daraus zurückrechnen - und weil Kohlenstoff so langsam zerfällt, geht das bis zu einem Alter von etwa 50.000 Jahren. Aufgabe: Auf einem Acker finden wir beim Spaziergang diesen Totenschädel. Die Analyse mit unserem in unsere Computermaus eingebauten C14-Detektor zeigt an, wie viel Prozent C14 noch im Fundstück übrig sind. Und es stellt sich die Frage: Wie alt ist der Schädel eigentlich? Weitere Aufgaben S. 90-92 Nr. 9 (exp!), 10, 11, 15, 12, 20 Biologische Wirkungen und Strahlungseinheiten: * Die Aktivität A Zur Charakterisierung der "Stärke" einer Strahlungsquelle verwendet man den Begriff der Aktivität. Sie beschreibt die Zahl der Zerfälle je Zeiteinheit. Zur Beschreibung der Wirkung der radioaktiven Strahlung auf einen Körper bedient man sich des Begriffs der Dosis. Dividiert man die Dosis durch die Zeit, so gelangt man zur Dosisleistung. * Energiedosis DE Je mehr Energie durch radioaktive Strahlung auf einen Körper übertragen wird, desto größer ist die - meist schädliche - Wirkung. Die Energiedosis ist der Quotient aus der absorbierten Energie ΔE und der Masse Δm des absorbierenden Körpers. * Ionendosis DI Die Ionendosis ist der Quotient aus der durch die Strahlung im Körper entstandenen elektrischen Ladung ΔQ und der Masse Δm des absorbierenden Körpers. * Äquivalentdosis H Die Äquivalentdosis berücksichtigt neben der Energieabgabe an den Körper auch noch die unterschiedliche Wirkung verschiedener Strahlenarten auf das Zellgewebe eines lebenden Organismus, indem die Energiedosis mit einem Bewertungsfaktor q multipliziert wird. H = q·DE Nach den neueren Bestimmungen der Strahlschutzverordnung ist eine effektive Dosis zu berechnen, die sich aus den summierten Äquivalentdosen für jedes Organ zusammensetzt, wobei die Organdosen noch jeweils mit einem Gewebe-Wichtungsfaktor w zu multiplizieren sind. Man sieht, dass diejenigen Organe mit schneller Zellbildung besonders gefährdet sind. Die Strahlenbelastung des Menschen: Aufgaben dazu S. 92 Nr. 23, 25 (PC!) Kernumwandlungen und Energiebilanzen Einstein fand folgende Formel als Beziehung zwischen Masse und Energie: E = m c2 (c = Lichtgeschwindigkeit) Zerlegt man einen Kern bestehend aus Z Protonen und N Neutronen in seine Bestandteile und sind die Kernbausteine (Nukleonen) soweit voneinander entfernt, dass weder die elektrische Abstoßungskraft zwischen den Protonen noch die starke Kernkraft zwischen den Nukleonen eine Rolle spielen, so ist die Gesamtenergie Evor der Bausteine nach der Einsteinschen MasseEnergie-Beziehung zu berechnen: Baut man die Nukleonen zu einem Kern X zusammen, so verliert das System aufgrund der anziehenden Kräfte zwischen Nukleonen an Energie, die Gesamtenergie nach dem Zusammenbau Enach wird nun kleiner sein. Wegen der Äquivalenz von Masse und Energie wird auch die Masse mk der Kerns kleiner sein als die Summe der Massen der Einzelbaustein. Für Enach gilt: Je stärker die Bindungskräfte zwischen den zum Kern zusammengefügten Nukleonen ist, desto kleiner wird der Betrag von Enach ausfallen. Die Energiedifferenz Ea - Ee wird als Bindungsenergie B des Kerns bezeichnet. Es gilt: Wie du auf der Grundwissensseite zur Einsteinschen Beziehung gelernt hast, ist der Ausdruck in der eckigen Klammer aber gerade der Massendefekt Δm. Somit gilt: Bindungsenergie: Die Bindungsenergie ist die beim Zusammenbau eines Kerns aus seinen Einzelbausteinen freiwerdende Energie. Sie hat ein positives Vorzeichen (exothermer Vorgang). Unter der mittleren Bindungsenergie pro Nukleon versteht man die Bindungsenergie bezogen auf ein Nukleon. Die mittlere Bindungsenergie hat den Wert B/A. Dabei ist A die Nukleonenoder auch Massezahl. Bei der Kernspaltung macht man sich diese Bindungsenergien zunutze: Bei einer Kernspaltung wird z.B. ein U-235-Kern durch ein Neutron gespalten. Die Reaktionsprodukte sind zwei leichtere Kerne und Neutronen. Wesentlich bei dieser exothermen Reaktion ist, dass die Summe der kinetischen Energien der Endprodukte größer ist als die Summe der kinetischen Energie der Anfangsprodukte. Was auf den ersten Blick wie eine Verletzung des Energiesatzes aussieht, wird mit der aus der Einsteinschen Relativitätstheorie gewonnen Erkenntnis, dass Masse und Energie gleichwertig (äquivalent) sind, verständlich: Untersucht man nämlich durch geeignete Apparate (Massenspektrometer) die Massen der Reaktionsprodukte, so stellt man fest, dass die Summe der Massen der Endprodukte (m nach) kleiner ist als die der Anfangsprodukte (mvor). * Die Massenunterschiede bei einer Spaltreaktion sind natürlich nicht so hoch, dass man sie mit einer auch noch so empfindlichen Balkenwaage feststellen könnte. Hierzu bedarf es ausgefeilterer Techniken, welche du erst in der Oberstufe kennenlernen wirst. * Wenn hier von Massen die Rede ist, so ist stets die sogenannte Ruhemasse eines Teilchens gemeint (Masse des Teilchens bei der Geschwindigkeit Null). Einstein stellte nämlich in seiner Relativitätstheorie fest, dass die Masse von Teilchen eine geschwindigkeitsabhängige Größe ist. * In der Teilchenphysik gibt man die Masse von Teilchen meist als Vielfaches der atomaren Masseneinheit u an. * Die Differenz zwischen der Massensumme der Teilchen vor der Reaktion mvor und der Massensumme der Teilchen nach der Reaktion mnach wird als Massendefekt Δm bezeichnet. Δm = mvor - mnach Die Einsteinsche Masse-Energie-Beziehung: Enach - Evor = (mvor - mnach)·c2 Man sagt auch, dass die Beziehung ΔE = Δm·c2 die Äquivalenz von Masse und Energie beschreibt. Energie und Masse sind nur zwei verschiedene "Währungen" des Gleichen. Der Umrechnungsfaktor zwischen diesen "Währungen" ist das Quadrat der Lichtgeschwindigkeit c (c = 2,998·108m/s ≈ 3,0·108m/s). 1. Beispiel: Atomare Masseneinheit Die atomare Masseneinheit 1 u = 1,6605·10-27 kg wird oft in Form einer Energie angegeben. Es gilt: 2. Beispiel: Energie bei der Spaltung von U-235 geg.: Atommassen der Teilchen Vernachlässigungen: Um die kinetische Energie der Reaktionsprodukte abschätzen zu können, nehmen wir an, dass das die Spaltung auslösende Neutron eine vernachlässigbare kinetische Energie besitzt. Außerdem ignorieren wir, dass die Reaktionsprodukte angeregt sind. Bestimmung des Massendefekts: Abschätzung der kinetischen Energie der Reaktionsprodukte: Bei der Kernfusion von Deuterium (Wasserstoffisotop mit einem Neutron und einem Proton im Kern) und Tritium (Wasserstoffisotop mit zwei Neutronen und einem Proton im Kern) entsteht (vereinfacht) ein Heliumkern und ein Neutron. Aufgabe: Bestätige durch Rechnung die Reaktionsenergie von ca. 17,6 MeV bei der oben dargestellten Fusionsreaktion. Warum ist die kinetische Energie der Reaktionsprodukte größer als 17,6 MeV? Aufgaben Buch S. 105 Nr. 2, 3, 4, 5, 6, 7, 8, 12, 13, 19, 20(?)