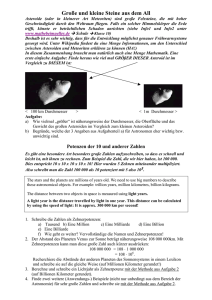
Übungsangebot Sequenz Wurzel und Potenzen für 9. Klasse

Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Potenzen mit ganzzahligen Exponenten
Werden zwei Potenzen mit gleicher Basis multipliziert/ dividiert, so gilt:
𝑎𝑚 · 𝑎𝑛 = am+n wobei 𝑎 ∈ ℝ; 𝑚, 𝑛 ∈ ℕ
am/ an = am-n
Werden zwei Potenzen mit unterschiedlicher Basis und unterschiedlichen Exponenten multipliziert/
dividiert, so gilt:
𝒂𝒎 · 𝒃𝒎 = (𝒂 · 𝒃)𝒎
am /bm = (a/b)m
Exponenten werden multipliziert:
(𝒂𝒎 )𝒏 = 𝒂𝒎·𝒏
Besondere Potenzen:
ao = 1 und a1 = a
Für negative Exponenten gilt:
𝟏
a-k := 𝒂
Aufgabe 1:
Berechne die Potenzen im Kopf.
a) 25
b) 33
c) (−4)3
d) 1,52
e) −210
54
f)
g) (−6)3
h) −63
Aufgabe 2:
Berechne die folgenden Potenzen.
a)
92
e) 122
b) 52
f)
152
c)
82
d) 102
g)
192
h) 202
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Aufgabe 3:
Schreibe die Terme ohne Klammern und ohne Potenzen.
a) (𝑎 + 𝑏)3
b) 2𝑏 3 + (3𝑎)2
c) (1𝑎2 𝑏)3
d) (−3)5 · 𝑎2
e) 4𝑎4 : (2𝑎)2
f)
(15𝑎6 )2
g) (82 · 43 ): (−2)10
h) 3 · 35 − 34
Aufgabe 4:
Schreibe als Potenz mit negativem Exponenten.
a)
1
26
b)
1
43
c)
1
75
d)
1
103
e)
1
32
f)
1
65
g)
1
𝑏6
h)
1
𝑎3
Aufgabe 5:
Schreibe mit positivem Exponenten.
a) 3−3
b) 3−2
e) 𝑎−6
f)
Aufgabe 6:
Berechne im Kopf.
a)
56 · 5−4
b)
2−12 · 29
c)
0,111 · 0,1−9
d)
(4) · (4)
e)
3−4
3−7
1 6
1 −4
3𝑏 −10
c) 4−5
d) 15−7
g) (7𝑏)−5
h) −3𝑎−4
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
f)
10−5
10−4
g)
11−6 : 11−8
2
h)
(2−3 ) ·23
2−4
−4
i)
(52 )
2
·(53 )
5−2 ·5−2
Zehnerpotenzen
Aufgabe 1:
In der Physik sind folgende Längeneinheiten gebräuchlich. Gib sie als Zehnerpotenzen mit der Einheit
m an.
1
i)
1 Mikrometer (1 µm) 1 µm = 1000 mm
j)
1 Nanometer (1 nm) 1 nm =
1
1000000
mm
1
k) 1 Picometer (1 pm) 1 pm = 1000000000 mm
Aufgabe 2:
Stelle folgende Zahlen mit Zehnerpotenzen dar.
Beispiel: 0,0004 = 4 · 0,0001 = 4 · 10−4
j)
0,00007
k) 0,000000009
l)
0,0038
m) 0,000000067
n) 0,0000001
i)
0,003
Aufgabe 3:
Schreibe die Längen in der angegebenen Einheit. Benutze dabei Zehnerpotenzen.
Beispiel: 1 cm = 0,00001 km = 10−5 km
a) 1 cm (m)
b) 1 mm (m)
c) 1 mm (km)
d) 72 dm (km)
e) 115 mm (km)
f)
172 m (km)
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Aufgabe 4:
Notiere die Größen ohne Zehnerpotenzen.
a) Fläche von Australien und Ozanien: 8,509 · 106 km2.
b) Zahl der Synapsen im Gehirn: 7 · 1012.
c) Durchmesser eines roten Blutkörperchens: 7,5 · 10−3 mm.
d) Masse eines Wasserstoffmoleküls: 3,35 · 10−24 g.
Aufgabe 5:
Schreibe als Zehnerpotenz.
j)
0,0001
k) 0,01
l)
0,00001
m) 1
n) 0,000000001
o) 0,00000000001
p) 0,0001
i)
0,1
Aufgabe 6:
Schreibe ohne Zehnerpotenz.
i)
Durchmesser der roten Blutkörperchen 7 · 10−4 cm
j)
Länge der kleinsten Bakterien ≈ 10−4 cm
k) Durchmesser des Wasserstoffatoms ≈ 10−8 cm
l)
Durchmesser des Atomkerns von Wasserstoff ≈ 10−12 cm
m) Gewicht eines Boratoms ≈ 17,952 · 10−24 g
Aufgabe 7:
Die Eiserne Brücke in Regensburg ist eine 82 m lange Bogenkonstruktion aus Stahl (gemessen bei
0°C). Bei einer Erwärmung um 1°C dehnt sich 1 m Stahl um 1,2 · 10−5 m aus.
j)
Um wie viel m (cm, mm) unterscheidet
sich die Brückenlänge im Winter (bei
−25°C) und im Sommer (bei +35°C)?
k) Wie groß wäre der Unterschied bei
einer Brückenlänge von 450 m?
l)
Wie würdest du ein Reißen der Brücke
verhindern?
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Aufgabe 8:
Schreibe in wissenschaftlicher Schreibweise.
a) 450000
b) 35670000
c) 0,00028
d) 86000
e) 0,0804
f)
6703000
g) 0,000024
h) 750200
i)
0,00206
Wurzeln
Für alle reellen Zahlen 𝑎, 𝑏 ≥ 0 mit 𝑏 ≠ 0 gilt:
𝑛 𝑚
𝑛
√ √𝑎 = √ 𝑚√𝑎 =
𝑛 •𝑚
√𝑎 ;
𝑛
√𝑎
√𝑏
𝑎
𝑛
𝑛
𝑛
= √𝑏 ; √𝑎 • √𝑏 = √𝑎𝑏
𝑛
( √𝑎 )m = √𝑎m
Für alle reellen Zahlen 𝑎, 𝑏 > 0 gilt: √𝑎 + √𝑏 > √𝑎 + 𝑏
Aufgabe 1:
Bringe den Faktor unter die Wurzel.
Beispiel: 3√2 = √3 · 3 · 2 = √18
m) 4√3
n) 5√7
o) 7√10
p) 0,1√12
q) 𝑎√𝑏
r) 2𝑥√0,5𝑦
s) 0,2𝑑√8
t) 1,5𝑠√3𝑠
l)
2√5
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Aufgabe 2:
Beseitige durch Erweitern die Wurzel im Nenner.
o)
3
√5
p)
4
√2
q)
t) √5
r)
√11
√7
s)
10√5
√10
u)
2·√3
3·√2
v)
5 3
√
3 5
x)
4·√5+3·√8
√20
y)
2√3−3√2
√6
√2
√3
2
w)
√8−3
√2
i)
8− 4
k) 𝑥 −2
l)
𝑐6
n) 0,1−1,1
o) 𝑎1,6
Aufgabe 3:
Schreibe als Wurzel.
4
2
h) 0,55
g) 43
4
j)
0,1−3
m) 3−0,4
3
0,3
3
q) 𝑧 − 2
p) 𝑦 9
3
5
r) 𝑝−5,6
Aufgabe 4:
Berechne ohne Verwendung des Taschenrechners.
e)
√18 · √8
f)
3
g)
√243: √3
h)
4
i)
√0,3 · √2,7
j)
3
√2 · √32
4
√80: √5
4
√√256
Aufgabe 5:
Rechne vorteilhaft.
Beispiel: √2 · √8 = √2 · 8 = √16 = 4
q) √5 · √20
r) √6 · √24
s) √8 · √32
t) √5 · √45
u) √6 · √54
v) √8 · √98
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Aufgabe 6:
Vereinfache.
6
n) √𝑎8
o) √𝑥 −15
q) (𝑥 −0,3 )1,2
r) ( √𝑥 )
3
4
6
s)
5
√𝑎−10
Aufgabe 7:
Fasse, wenn möglich, zusammen und berechne auf zwei Dezimalstellen genau.
m) √8 + √8
n) 4√7 − √7
o) 5√5 − 8√5
p) 11√3 + 9√3
1
12
p) (√𝑎3 )
q) 2√20 − √20
3
r) 3,5√32 − √32
s) 8√7 − 12,4√7
t) √3 + √4
u) 2√5 − 3√6
v) 7√9 − 1,4√8
w) 6,4√13 + 7,2√12
x) 0,5√20 + 0,5√21
y) 19√36 − 24√30
z) 13,2√28 − 0,9√25
Lehrer: Neuhold
Klasse: 9a
Datum: 12.09.143
Potenzen mit rationalen Exponenten
𝑚
𝑛
𝑎 𝑛 = √𝑎
Aufgabe 1:
Schreibe als Potenz.
5
a) √34
−6
d) (√0,5)
1
8
( 5√0,9)
c)
7
5
1
e) √(4)
f)
8
9
3
4
g) √(5)
j)
7
3
b) (√5)
h)
3
(√2)
k)
4
4
1
√6,59
i)
l)
3
√0,5−5
11
2
(√3)
6
1
4
√53
1
5
(√12)
Aufgabe 2:
Schreibe als Wurzel.
4
2
b) 0,55
a) 43
4
3
c) 8−4
3
5
d) 0,1−3
e) 𝑥 −2
f)
𝑐6
g) 3−0,4
h) 0,1−1,1
i)
𝑎1,6
l)
𝑝−5,6
3
j)
𝑦9
0,3
k) 𝑧 − 2