Werkstatt Arbeit PS 1409 - Physic

Werkstatt: Arbeit = Kraft ⋅ Weg
Viel Kraft für nichts?
In der Physik definiert man Arbeit durch das Produkt aus Kraft und Weg:
W = 𝐹⃗ * 𝑠⃗ = FII * s

FII bezeichnet dabei die Kraftkomponente in Wegrichtung s. Die Einheit der Arbeit ist das Joule (J).
In Worten versteht man unter der Arbeit folgendes:
Es wird physikalische Arbeit verrichtet, wenn eine Kraft längs eines Weges
bzw.
Mit in entgegengesetzter Richtung zu einem Kraftfeld wirkt.
Was ist mit „längs“ des Weges gemeint? Heisst das, dass keine Arbeit im physikalischen Sinne verrichtet wird,
wenn eine Kraft zum Beispiel senkrecht zu einer Wegstrecke wirkt? Ja, genau! Trägt man zum Beispiel einen
Koffer während man vorwärts geht, wird keine Arbeit verrichtet, da Kraft und Weg senkrecht zueinander
stehen (siehe Fig.). Für die physikalische Arbeit ist also nur die Kraft relevant, die entlang, d.h. in Richtung des
Weges wirkt!
Fig.: G ist die Gewichtskraft des
Koffers. Sie zeigt senkrecht zum
Weg nach unten.
Wie kann man das verstehen? Nun, einerseits ist es eine Definition, die sich in der Physik bewährt hat.
Andererseits können wir die Definition auch mathematisch interpretieren: Das Produkt aus Kraft und Weg ist
ja kein gewöhnliches mathematisches Produkt. Da sowohl die Kraft als auch der Weg ein Vektor ist, werden
also zwei Vektoren miteinander multipliziert! Wie soll das gehen? In der Mathematik spricht man hier vom
sogenannten Skalarprodukt. Dabei werden zwei Vektoren so multipliziert, dass am Schluss eine Zahl (Skalar)
herauskommt. Für die Arbeit sieht das so aus:
W = 𝐹⃗ * 𝑠⃗ = F* s *cos( α )



s

F
Für die Arbeit ist nur die Kraft

relevant, die in Wegrichtung zeigt.
Sie beträgt FII = F⋅ cos(α).
F II
Die Arbeit ist somit eigentlich das Produkt aus der Kraftkomponente in Wegrichtung und dem Weg. Der
Winkel α ist dabei der Winkel, der zwischen dem Kraftvektor und dem Wegvektor liegt. Ist α = 90 o, d.h. stehen
die beiden Vektoren senkrecht aufeinander, so ist cos(α) = 0 und somit ist auch W = F*s*cos(α) = 0. Es wird also
keine Arbeit verrichtet. Merken Sie sich also
Wirkt die Kraft senkrecht zur Wegrichtung, so wird keine Arbeit verrichtet.
Aufgabe 1
Geben Sie die SI-Einheit der Arbeit an.
Aufgabe 2
Ein Kind zieht einen Schlitten auf dem Eis. Dafür braucht es eine Kraft von 100 N. Die Leine des Schlittens
schliesst mit dem Eisboden einen Winkel von 40o ein. Welche Arbeit verrichtet das Kind, wenn es einen Weg
von 20 m zurücklegt? (1530 Nm )
Aufgabe 3
Nennen Sie Situationen, in denen ein Körper bewegt ist und dabei keine Arbeit verrichtet wird.
Zum Nachlesen und – schauen:
http://wikis.zum.de/zum/Benutzer:Zoliverz/Lernpfad_Energie/1._Physikalische_Arbeit__Zieh_Dein_Skateboard_auf_die_Rampe!
Werkstatt: Arbeit = Kraft ⋅ Weg
Hubarbeit W = m g h
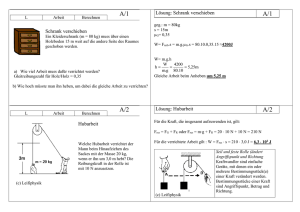
Die Abbildung zeigt einen Mann, der ein schweres Fass
auf einen Wagen verladen will. Er hebt die Last
senkrecht hoch, übt also eine Kraft längs eines
bestimmten Weges aus. Die Kraft, die er aufwenden
muss, entspricht der Gewichtskraft F des Fasses. Der
zurückgelegte Weg ist die Höhe h vom Boden bis hinauf
zur Ladefläche des Wagens.
Da hier ein Gegenstand auf eine gewisse Höhe gehoben
wird, spricht man auch von Hubarbeit. Sie berechnet
sich folgendermassen:
W = F II ⋅s = m g h
,
wobei m die Masse des Gegenstandes, g die Fallbeschleunigung (9.81 m/s 2) und h die Höhe bezeichnet.
Die Hubarbeit ist also das Produkt aus der Gewichtskraft F = m ⋅ g und dem Weg, bzw. der Höhe h.
Aufgabe 4:
Berechnen Sie die Hubarbeit die der Mann in der Abbildung verrichtet, wenn er das 20 kg schwere Fass auf die
1.2 m hohe Ladefläche hebt. (240 Nm)
Aufgabe 5:
Das Verladen der Fässer liesse sich auch anders
durchführen: das Fass bräuchte nicht gehoben, es
könnte viel leichter über ein schräg gestelltes Brett
hinaufgerollt werden. Der Winkel zwischen dem Brett
und dem Boden beträgt 45o. Die Reibung kann
vernachlässigt werden.
Berechnen Sie
a) die Kraftkomponente FII parallel zum Weg s
(Brett), (141 __ )
b) den zurückgelegten Weg s, (1,7 m )
c) die verrichtete Arbeit W. (240 __ )
d) Was fällt Ihnen auf? Was kann so gespart werden, was nicht?
e)* Setzen Sie nun als Beweis für Ihre Vermutung die Formeln aus a) bis c) (ohne Zahlen) für die
verrichtete Arbeit zusammen. Alles klar?!
Aufgabe 6
Studieren Sie zur sogenannten „goldenen Regel der Mechanik“ folgende Internetseite:
http://www.leifiphysik.de/themenbereiche/arbeit-energie-undleistung#Goldene%20Regel%20der%20Mechanik (Google „Leifi Goldene Regel Mechanik“)
Beantworten Sie dann folgende Fragen:
a) Was besagt die goldene Regel der Mechanik?
b) Nennen Sie drei Kraftwandler!
Aufgabe 7
Überprüfen Sie die goldene Regel der Mechanik am Flaschenzug, der bei der Lehrperson steht.
Zusatzaufgaben: Aufgaben 217 und 218 S. 72 im Aufgabenbuch
Seite 2 von 6
Werkstatt: Arbeit = Kraft ⋅ Weg
Reibungsarbeit W = FR⋅ s
Jeder hat schon einmal versucht, ein schweres Möbelstück von seinem Platz zu verrücken. Die Kraft, die man
dabei aufwendet, muss die Reibung der Berührungszonen von Möbelstücken überwinden.
Die Arbeit, die man gegen die Reibung verrichtet, berechnet sich aus dem Produkt von Reibungskraft FR und
dem Weg s:
W = F II s = F R s
Aufgabe 8
Ein Kind der Masse 20 kg sitzt auf einem 2 kg schweren Schlitten. Berechnen Sie die notwendige Arbeit, um
den Schlitten mit dem Kind 50 m zu schieben, wenn der Reibungskoeffizient zwischen den Kufen und dem
Neuschnee 0.4 beträgt. (4.400 ___ )
Zusatzaufgabe
Aufg. 220 S. 73 im Aufgabenbuch
Seite 3 von 6
Werkstatt: Arbeit = Kraft ⋅ Weg
Verformungsarbeit W = ½Ds
2
Unter Verformungsarbeit kann man sich vereinfacht die Arbeit vorstellen, die nötig ist, um eine Feder zu
komprimieren oder zu dehnen.
Beispiel: Eine Schraubenfeder mit der Federkonstante D wird
um die Strecke s gedehnt. Für diese Dehnung
müssen wir eine Kraft aufwenden. Die Kraft ist aber nicht
konstant, sondern proportional zur Strecke s (Hooke’sches
Gesetz). Das heisst die Kraft wächst mit zunehmender
Dehnung.
D
Die Formel für Spann- bzw. Verformungsarbeit lässt sich
folgendermassen begründen:
Aufgabe 9
Skizzieren Sie ein Diagramm mit der Spannkraft F auf der yAchse und der Dehnung s auf der s-Achse. Zeichnen Sie nun
qualitativ die Spannkraft in Abhängigkeit der Dehnung s ein
(Hooke´sches Gesetzt F = D s).
Die Arbeit ist als Produkt von Kraft und Weg definiert.
* (i) Berechnen Sie nun anhand dieses Diagramms die an
einer Feder verrichtete Arbeit.
(ii) Zeichnen Sie nun im Diagramm die der Arbeit
entsprechende geometrische „Größe“ ein.
Hinweis: Versuchen Sie die Aufgabe zu lösen. Wenn Sie die
Lösung nach einiger Zeit nicht finden, lesen Sie den folgenden
Abschnitt. Probieren Sie es dann noch einmal mit dieser
Aufgabe.
Formel für die Berechnung der an einer Feder verrichteten Arbeit:
Geometrische Größe, die im Diagramm den Betrag der Arbeit zeigt: ________________________
Wir müssen daher zur
Berechnung der Arbeit nicht etwa die Kraft F = D s nach vollendeter Dehnung einsetzen, sondern die mittlere
Kraft F = ½ D s
Die Arbeit wächst also nicht linear sondern ____________________ mit der Dehnung s!
Aufgabe 10
Lösen Sie die Aufgabe 224 S. 73 im Aufgabenbuch.
Werkstatt: Arbeit = Kraft * Weg
Beschleunigungsarbeit W = ½mv 2
Gemäss Newtons zweitem Gesetz (Grundgesetz der Mechanik) ist eine Kraft notwendig, um einen Körper zu
beschleunigen. Da die Kraft längs der beschleunigten Strecke wirkt, wird Arbeit verrichtet.
Beispiel: Ein Auto soll auf einer glatten, ebenen Fahrbahn in gleichmässig beschleunigte Bewegung versetzt
werden. Zur Beschleunigung wird die konstante Kraft F = m a benötigt. Das Auto erhält dadurch die
Geschwindigkeit
Für den zurückgelegten Weg erhält man
v=at
s = ½ a t²
Wenden wir nun den Arbeitsbegriff sinngemäss an, so ergibt sich:
W = F{{ *s = m a ½ a t²
=
½m(at)²
=
½ m v²
Die Arbeit nimmt also quadratisch zu mit der Geschwindigkeit v! Das heisst, dass sie das vierfache an Arbeit
(Treibstoff) benötigen um die doppelte Geschwindigkeit zu erreichen.
Aufgabe 11
Welche Arbeit müssen Sie aufwenden, wenn sie Ihr Fahrrad (Gesamtmasse 85 kg) von 0 km/h auf 36 km/h
beschleunigen möchten? (4,25 kN)
Aufgabe 12
a) Berechnen Sie die Arbeit die nötig ist, um ein Auto der Masse 1500 kg von 0 km/h auf 36 km/h zu
beschleunigen
b) Berechnen Sie die Arbeit die nötig ist, um ein Auto der Masse 1500 kg von 0 km/h auf 80 km/h zu
beschleunigen (370 kJ)
c) Berechnen Sie die Arbeit die nötig ist, um das Auto von 0 km/h auf 120 km/h zu beschleunigen. (833 kJ)
d) Berechnen Sie die Arbeit die nötig ist, um das Auto von 80 km/h auf 120 km/h zu beschleunigen. (463 kJ)
e) Vergleichen Sie die Ergebnisse aus b) bis d). Formulieren Sie eine Abhängig des Betrags der Arbeit zu den
absoluten Geschwindigkeiten.
Zusatzaufgabe
Aufgabe 221 S. 73 im Aufgabenbuch
Seite 5 von 6
Werkstatt: Arbeit = Kraft ⋅ Weg
Zusatz: Mehrere Kräfte wirken
Für gewöhnlich sind mehrere Kräfte zur Bewältigung einer Arbeit nötig. Betrachten Sie das folgende Beispiel
und lösen Sie anschliessend die Aufgabe:
Ein Skifahrer der Masse m = 75 kg wird mit einem Schlepplift hochgezogen. Das Starthaus des Skilifts befindet
sich auf 1800 m.ü.M. Das Ende des Skilifts ist auf 1950 m.ü.M, wo der Skifahrer nach einer 2 km langen Fahrt
eine konstante Geschwindigkeit von 9 km/h hat. Die Skier sind frisch gewachst und haben deshalb einen
kleinen Reibungskoeffizienten von 0.1.
Aufgabe
a) Nennen Sie alle Arbeitsformen die für die gesamte Arbeit des Lifts berücksichtigt werden müssen.
Schreiben Sie auch gleich die nötigen Formeln auf.
b) Berechnen Sie nun die gesamte vom Lift verrichtete Arbeit.
c) Was haben Sie vernachlässigt, bzw. was müsste man auch noch berücksichtigen, wenn man wissen
möchte, wie viel Arbeit der Lift an einem gut besuchten Tag verrichten soll?