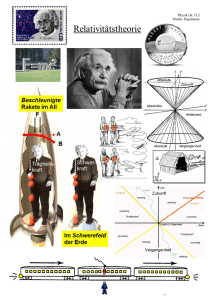
Wellenfronten bei bewegten Quellen

§11.13 Wellen bei bewegten Quellen
Doppler-Effekt
Bewegt sich die Quelle relativ zum Medium,
ändert sich für einen Beobachter die Schallfrequenz.
Während
der Schwingungsdauer T  1 f 0 durchläuft
.
die Welle in z-Richtung die Strecke  z   0  v Ph T
Bewegt sich die Quelle mit der Geschwindigkeit uQ  u z in z-Richtung auf den
Beobachter zu, so ist der Abstand Flächen gleicher Phase demnach:

   0  uQ T 

v Ph  u Q
f0
Der ruhende Beobachter misst
demnach die Frequenz f:
Dieser Abstand ist definitionsgemäß die Wellenlänge
der sich im Medium ausbreitenden Welle.
f 
v Ph


f0
Entsprechend für eine sich entfernende Quelle:
v Ph
v Ph  u Q

f0
f  f0
1
1  u Q v Ph
1
1  u Q v Ph
Doppler-Effekt
Bewegt Beobachter, ruhende Quelle:
In der Zeit T  1 f 0 bewegt sich der Beobachter
um die Strecke  z  u B T und misst deswegen
n   z  0 zusätzliche Schwingungen.
Die gemessene Frequenz erhöht sich damit um
  n T und wird :
f

f 
f0 
uB
0

f0 
f0
uB
v Ph
Entsprechend für eine
Bewegung von der Quelle weg:
Bewegen sich sowohl Quelle,
als auchBeobachter, wird die
gemessene Frequenz:
f0 

u B 
f 0 1 

v Ph 

f 

u B 
f 0 1 

v Ph 

f 
f0

Für beliebige Bewegungsrichtungen ergibt sich vektoriell:

Gaub
  0
1  u B v Ph
1 m u Q v Ph
0
0
r
 k
r
 k
r
uB
r
uQ
60
Doppler-Effekt
Einfach einsehbar ist dies aus der Wellendarstellung:
r r
  A cos  0 t  k r


Die Bewegungsgleichung des Bewegten Beobachters ist:
r
r
r
r  u B t  r0

Damit wird die Wellendarstellung:
r r
r r
r
  A cos  0 t  k u B t  r0   A cos  t  k r0


mit:    0




r r
 k uB

analog für eine Bewegung der Quelle

Gaub
WS2014/15
61
Wellenfronten bei bewegten Quellen
Bewegt sich eine Schallquelle mit der Geschwindigkeit u in z-Richtung und
sendet Kugelwellen mit der Frequenz f 0 aus, ist der Abstand λ zweier um 2π
versetzter Phasenflächen vom Winkel α gegen die Bewegungsrichtung
abhängig:
   
u
f0


v Ph  u cos  

Gaub
WS2014/15
62
Wellenfronten bei bewegten Quellen
Bewegt sich die Quelle mit der Phasengeschwindigkeit, wird    0   0
 Die Amplituden zu verschiedenen Zeiten ausgesandter Kugelwellen
überlagern sich und es entsteht eine Welle mit sehr großer Amplitude
(nicht mehr harmonisch!), die sogenannte Kopfwelle.

Bewegt sich die Quelle sogar schneller als die Phasengeschwindigkeit, ist

v Ph
   arccos 
 u


  0


Gaub
63
Wellenfronten bei bewegten Quellen
In diesem Fall sind die zu verschiedenen Zeiten ausgesandten Kugelwellen
auf Kegeln mit dem Öffnungswinkel β in Phase. Es ist:
  90   


sin   
v Ph
u

1
mit der Machzahl M
M
Der Kopfwellenkegel
heißt dann Machscher
Kegel.
Zu beobachten sind derartige Kegel zum Beispiel bei Schiffen, deren
Geschwindigkeit größer ist als die Phasengeschwindigkeit der
Oberflächenwellen des Wassers.
Man beachte aber die Dispersion der Wasserwellen!!!
64
Size doesn‘t matter!
65
And speed neither!
Wellenfronten bei bewegten Quellen
Ein Schiff bewege sich mit der Geschwindigkeit u und befinde sich zum
Zeitpunkt t = 0 am Punkt Q 1 . Dabei sendet es Oberflächenwellen in einem
breiten Spektrum aus. Hat das Schiff zum Zeitpunkt T den Punkt Q 2 erreicht,
habe die Welle mit der Mittenwellenlänge  0 den Punkt W 0 erreicht.

Da andere Teilwellen
andere Phasengeschwindigkeiten und damit andere

Phasen im Punkt W 0 haben, mittelt sich die Gesamtamplitude
zu Null und

es entsteht keine Kopfwelle. 
Das Maximum der Wellengruppe,
das sich mit der Gruppenge
schwindigkeit
v Gr 
1
2
v Ph  0 
bewegt, ist zum Zeitpunkt T erst
am Punkt G 0 , weshalb die
Q G
Bugwelle
 entlang der Linie 2 0
entsteht.


66

Wellenfronten bei bewegten Quellen
Mit Q 2W 0  d und Q 1G 0  s ergibt sich
2s
s
für den Öffnungswinkel θ der Bugwelle: tan  0  
und tan  0    
d
d
 
 
   arctan 2 s   arctan  s 
 d 
d 
 2 

 arctan 
  arctan 1 / 2
 2 
Weil Q unabhängig von s ist
sein muss 
gelten:
 0 
d arg  

d arg  ds
d
d
ds
1
0
1 
2d

d
2
4s
d
2
2
1

d
d
2
1
2
 s
2

2
2
2
 2
d  4s
d  s
2d  2s  d  4 s

2
2
d  2s
d
s 
2
2
2
2
   19 , 5
d
d 
d

2

2
s
1 
2
 4s
1
2


Unabhängig von der
Geschwindigkeit,
solange u > vph!
2
WS2014/15
67

Wellenfronten bei bewegten Quellen
Bei einem mit Überschallgeschwindigkeit fliegenden Flugzeug ist die
Kopfwelle als lauter Knall wahrnehmbar („Überschallknall“).
Die Krümmung der Wellenfronten hat mehrere Ursachen:
Das Flugzeug ist keine Punktquelle, die Schallgeschwindigkeit hängt
von der Höhe über dem Erdboden ab ( T(h), p(h) ).
Gaub
WS2014/15
68