M 9 Übungsaufgaben zum Satz des Pythagoras und zur
Werbung

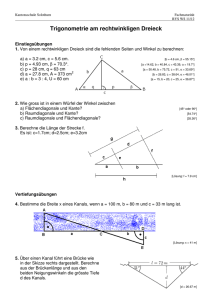
M9 Übungsaufgaben zum Satz des Pythagoras und zur Trigonometrie 1.)Ein Junge hält einen Drachen an einer 75 m langen Schnur ganz straff. Sein Freund steht 40 m von ihm entfernt und sieht den Drachen genau über sich. Berechne die Höhe des Drachens. 2.) In einem gleichseitigen Dreieck ist die Höhe 42 cm lang. Berechne die Seitenlänge s des Dreiecks zuerst in allgemeiner Form und setze dann den Zahlenwert für die Höhe ein. 3.) Landwirt Hühnerfroh besitzt ein Wiesenstück in Form eines gleichschenkligen Dreiecks. Das Areal ist 488,29 m² groß, die Grundseite 38,6 m lang. Die Wiesenfläche soll den Hühnern als Auslauf dienen. Deshalb wird sie eingezäunt. Wie viel Meter Zaun sind erforderlich? 4.) Ein Neubau mit Satteldach ist 11,4 m breit. Die Dachsparren haben eine Länge von 7,5 m. Allerdings ragen die Sparren 40 cm über die Hauswand hinaus. Welche Höhe hat der Hausgiebel? Fertige eine Skizze an. (Dachsparren = Balken) 5.) In und um einen Kreis mit dem Radius r = 3,6 cm ist je ein Quadrat gezeichnet; beide Quadrate berühren den Kreis. Wie lang sind die Quadratseiten des a) umbeschriebenen Quadrates? b) einbeschriebenen Quadrates? 6.) Ein Quader ist 7 cm lang, 5 cm breit und 4 cm hoch. Berechne die Länge der Diagonalen der 3 Seitenflächen sowie die Länge der Raumdiagonalen. Runde auf eine Stelle hinter dem Komma. 7.) Ein neuer Deich erhält das Profil eines Trapezes. Die seeseitige Böschung wird 35 m lang, die landseitige Böschung wird 21 m lang, die Höhe beträgt 13 m und die obere Breite (Deichkrone) beträgt 5 m. Wie breit wird der Deichfuß? (Untere Seite) 8.) Bei einer Pyramide mit quadratischer Grundfläche ist a die Grundkante, h die Höhe, s die Seitenkante, der Neigungswinkel der Seitenkante und ß der Neigungswinkel der Seitenfläche. Berechne die gesuchte Größe. a) h = 12 cm; s = 13 cm b) a = 8 cm; h = 10 cm c) s = 20 m; = 71,8° Gesucht: Gesucht: ß Gesucht: h und a 9.) Die Spitze eines direkt am Ufer eines Flusses stehenden 18 m hohen Baumes erscheint dem Beobachter am gegenüberliegenden Ufer unter einem Winkel von 48°. Wie breit ist an dieser Stelle der Fluss? 10.) Im Rechteck ABCD sind die Seiten a = 30 cm (150 m) und b = 18,6 cm (270,6 m) lang. Wie groß ist der Schnittwinkel der Diagonalen? Welchen Winkel 1 und 2 bilden die Diagonalen mit den Seiten? 11.) In einem Sumpfgelände ist die Entfernung zwischen zwei Punkten A und C nicht direkt messbar. Man hat deshalb von A aus eine Standlinie AB = s abgesteckt, von A und B den Punkt C angepeilt und die Winkel und ß zwischen der Standlinie und den Visierlinien gemessen: s = 800 m; = 84°, ß = 66°. Berechne die Entfernung zwischen A und C. Ergebnisse ab Mittwoch auf der PG-Homepage Ergebnisse : 1.) h = 63,44m s 3 1 2.) s2 = (2 )2 + h2 ; 4 s2 = h 2 ; s = 2h√3 ; s = 48,5cm 1 g 3.) A = 2 gh ; h = 25,3m ; s2 = ( 2 )2 + h2 ; s = 31,82m ; U = 95,46m 4.) Siehe auch Aufgabe 12/S.140 (Dachneigung = 29,90 ; Dachhöhe 3,0m) 11,4 2 ) 2 h2 = 7,12 – ( ; h = 4,23m 5.) Umbeschriebenes Quadrat : a1 = 2r = 7,2cm Einbeschriebenes Quadrat ( Die Ecken liege auf dem Kreis) : Durchmesser = Diagonale des Quadrats ; a2 = 5,1cm 6.) Siehe auch Aufgabe 33/S.109 d1 = 8,06cm ; d2 = 8,6cm ; d3 = 6,4cm ; Raumdiagonale d = 9,5cm 7.) Zeichne an geeigneten Stellen die Höhe h ein, so dass du 2 rechtwinklige Dreiecke und ein Rechteck erhältst. Untere Breite = 5m + 32,5m + 16,5m = 54m 8.)Siehe auch Aufgabe 14/Seite 140 ; = 67,380 ; = 6,2cm ( ist hier der untere Winkel im Gegensatz zur Bezeichnung im Buch) H = 19cm ; a = 8,84cm 9.) 16,21m 10.) 0,5a 2 0,5b a tan 2 b 30 (1) tan 1,6129 2 18,6 58,20 2 116,40 (2) 58 tan Berechnung von 1: (1) 1 = 90° – 58,2° = 31,8 ° (2) 2 = 90° – 29° = 61° Berechnung von 2: (1) 2 = 90° – 1 = 58,2° (2) 2 = 90° – 61° = 29° 11.) mit Sinussatz : AC s sin66 = sin30 ; AC = 1461m