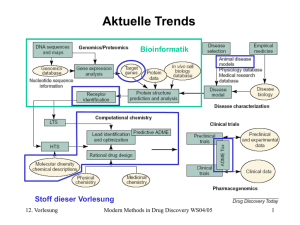
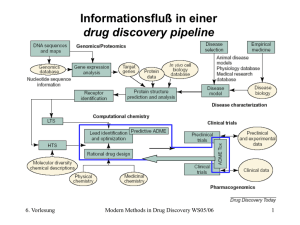
Modern Methods in Drug Discovery
Werbung

QSAR, QSPR, Statistik, Korrelation, Similarität & Deskriptoren Das Handwerkszeug des rational drug designs am Computer, vor allem dann, wenn keine Strukturinformation über das target (Enzym) vorhanden ist. QSAR-Gleichungen stellen einen quantitativen Zusammenhang zwischen chemischer Struktur und (biologischer) Aktivität her. log( 1 / C ) k1 P1 k2 P2 kn Pn Erfordert das Vorhandensein von experimentellen Meßdaten für eine Reihe von bekannten Verbindungen, z.B. aus High Throughput Screening 6. Vorlesung Modern Methods in Drug Discovery WS04/05 1 Begriffsdefinitionen QSAR: quantitative structure-activity relationsship QSRP: quantitative structure-property relationship Activity und Property sind z.B: log(1/Ki) Bindungskonstante log(1/IC50) Konzentration bei der 50% Wirkung eintritt Physikalische Größen, wie Siedepunkt, Löslichkeit, … Ziel: Voraussage von Moleküleigenschaften anhand ihrer Struktur, ohne eine expt. Meßung durchführen zu müßen. → in silico anstatt in vitro oder in vivo Vorteil: Einsparung von Zeit und Resourcen 6. Vorlesung Modern Methods in Drug Discovery WS04/05 2 Zeitliche Entwicklung von QSAR Methoden (I) 1868 Aber: A.C.Brown, T.Fraser: Physiologische Aktivität ist eine Funktion der chemischen Konstitution (Zusammensetzung) Eine direkte Beziehung ist nicht gegeben, sodern immer nur über die Unterschiede. Zur Erinnerung: 1865 Strukturvorschlag für Benzol von A. Kekulé Die chemische Struktur der meisten organischen Verbindungen ist noch unbekannt ! 1893 6. Vorlesung H.H.Meyer, C.E.Overton Toxizität von organischen Verbindungen steht im Verhältnis zu deren Verteilung zwischen wäßrigem und lipophilen biologischem Medium Modern Methods in Drug Discovery WS04/05 3 Zeitliche Entwicklung von QSAR Methoden (II) 1868 E.Fischer Schlüssel-Schloß Prinzip bei Enzymen Widerum keinerlei strukturelle Information über Enzyme vorhanden ! 1930-40 Hammet Gleichung: Reaktivität physikalisch, organische, theoretische Chemie 1964 C.Hansch, J.W.Wilson, S.M.Free, F.Fujita Geburtsstunde der modernen QSAR-Methoden Hansch-Analyse bzw. Free-Wilson-Analyse log( 1 / C ) k1 P1 k2 P2 kn Pn Koeffizienten (konstant) Deskriptoren oder Variablen linear free energy-related approach 6. Vorlesung Modern Methods in Drug Discovery WS04/05 4 Deskriptoren Ansätze eine mathematische Beziehung zwischen numerischen Eigenschaften (Deskriptoren Pi) und physikochemischen Eigenschaften der Verbindung (z.B. biologische Aktivität log(1/C) ) herzustellen, werden als QSAR, bzw QSPR bezeichnet. log( 1 / C ) k1 P1 k2 P2 kn Pn Daneben werden Deskriptoren auch zur Beschreibung von Molekülen in der Diversitäts Analyse und in Kombinatorischen Bibliotheken eingesetzt. Prinzipiell kann jede molekulare Eigenschaft als Deskriptor verwendet werden. Mehr zu Deskriptoren unter http://www.chemcomp.com/Journal_of_CCG/Features/descrip.html 6. Vorlesung Modern Methods in Drug Discovery WS04/05 5 Informationsfluß in einer drug discovery pipeline 6. Vorlesung Modern Methods in Drug Discovery WS04/05 6 Zunehmende Information Komponentenauswahl Wieviel Information ist über das target vorhanden ? X-Ray mit Wirkstoff Docking HTS X-Ray des Proteins active site Reihe von wirksamen QSAR, Verbindungen Pharmacophor erstellen Wenige hits aus HTS Kenntnis der Enzymfunktion (z.B. Kinase, GPCR) eADME Filter combi chem Erstellen einer virtuellen Bibliothek 6. Vorlesung Modern Methods in Drug Discovery WS04/05 7 Molekülbasierte Deskriptoren zur Voraussage der ADME Eigenschaften logP Wasser/Octanol Verteilungskoeffizient Lipinski‘s rule Topologische Indices Polar surface area Similarität / Dissimilarität QSAR quantitative structure activity relationship QSPR quantitative structure property rel. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 8 „1D“ Deskriptoren (I) Für einige Deskriptoren benötigt man nur Kenntnisse die sich bereits aus der Summenformel der Verbindung erhält. Bsp.: Molmasse, Gesamtladung, Anzahl von Halogenatomen Weitere solcher eindimensionaler Deskriptoren ergeben sich additiv aus atomaren Beiträgen. Bsp.: Summe der atomaren Polarisierbarkeiten Refraktivität (Brechungsindex n, molar refractivity, MR) MR = (n2 –1) MW / (n2 +2) d mit Dichte d, Molekülgewicht MW Ist abhängig von der Polarisierbarkeit und enthält außerdem das Molekülvolumen (MW / d) 6. Vorlesung Modern Methods in Drug Discovery WS04/05 9 logP (I) Der Wasser/n-Octanol Verteilungskoeffizient bzw. der logaritmierte Wert wird als logP bezeichnet. Wird oft zur Abschätzung der Membrangängigkeit und der Bioverfügbarkeit einer Verbindung eingesetzt, da ein oral applizierter Wirkstoff lipophil genug sein muß um durch die Lipidschicht der Membrane zu gelangen, andererseits wasserlöslich sein muß um in Blut und Lymphe transportiert zu werden hydrophil –4.0 < logP < +8.0 lipophil Zitronensäure –1.72 Typische Wirkstoffe < 5.0 6. Vorlesung Iodbenzol +3.25 Modern Methods in Drug Discovery WS04/05 10 logP (II) Zur Vorhersage des logP wurde eine Reihe von Methoden entwickelt: basierend auf Molekülfragmenten (Gruppen und Reste) ClogP Leo, Hansch et al. J.Med.Chem. 18 (1975) 865. Problem: Aufreten von nicht parametrisierten Fragmenten (bis zu 25% in Substanzbibliotheken) basierend auf Atomtypen SlogP S.A. Wildman & G.M.Crippen J.Chem.Inf.Comput.Sci. 39 (1999) 868. AlogP, MlogP, XlogP... Jeweils mittels einer mathematischen Fitprozedur (Regressionanalyse, Neuronales Netz) erstellt. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 11 logP (III) Neuere Methoden zur Vorhersage des logP verwenden zunehmend Eigenschaften des kompletten Moleküls, wie etwa Moleküloberfläche (polare/unpolare, bzw.deren elektrostatische Eigenschaften) Dipolmoment und Polarisierbarkeit Volumen / Oberfläche (Globularität) Bsp: mit Hilfe quantenmechanischer Daten trainiertes Neuronales Netz logP T. Clark et al. J.Mol.Model. 3 (1997) 142. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 12 „1D“ Deskriptoren (II) Weitere atomare Deskriptoren benutzen Information basierend auf empirischen Atomtypen wie in einem Kraftfeld. Bsp.: Anzahl von Halogenen Anzahl von sp3 substituierten Kohlenstoffatomen Anzahl von H-Brücken Akzeptoren (N, O, S) Anzahl von H-Brücken Donoren (OH, NH, SH) Anzahl aromatischer Ringe Anzahl von COOH Gruppen ... Anzahl frei drehbarer Bindungen 6. Vorlesung Modern Methods in Drug Discovery WS04/05 13 fingerprints Binärer fingerprint eines Moleküls 6. Vorlesung Modern Methods in Drug Discovery WS04/05 14 Lipinski´s Rule of 5 Kombination von Deskriptoren zur Abschätzung der intestinalen Absorption. Schlechte Aufnahme der Verbindung, wenn Molekülmasse > 500 logP > 5.0 > 5 H-Brücken Donoren (OH und NH) >10 H-Brücken Akzeptoren (N und O) Schlechte Diffusion Zu lipophil Zuviele H-Brücken mit den Kopfgruppen der Membran C.A. Lipinski et al. Adv. Drug. Delivery Reviews 23 (1997) 3. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 15 2D Deskriptoren (I) Bei Deskriptoren die sich aus der Molekülkonfiguration (kovalente Verknüpfung der Atome) ableiten, spricht man von 2D Deskriptoren. Da keine Atomkoordinaten verwendet werden sind 2D Deskriptoren generell konformationsunabhängig C1 obwohl sie topologische H2 Information über das H3 H4 Molekül enthalten. Vgl. Darstellung mittels SMILES C 5 O7 H4 Modern Methods in Drug Discovery WS04/05 H6 C1 H2 adjacency matrix 0 1 1 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 H6 0 0 0 0 1 O7 0 0 0 0 1 6. Vorlesung C5 H3 M 0 0 0 0 1 0 0 0 0 0 0 1 0 0 distance 0 1 1 1 0 2 1 2 0 1 2 2 1 2 2 2 3 3 2 3 3 matrix 1 1 2 2 2 2 0 2 2 0 3 1 3 1 D 2 3 3 3 1 0 2 16 2 3 3 3 1 2 0 2D Deskriptoren (II) Die wesentlichsten topologischen Eigenschaften eines Moleküls sind der Verzeigungsgrad und die molekulare Form. O7 H4 H2 C5 Für Kohlenstoff stehen 4 Valenzen zur Verfügung. H6 C1 H3 Das Verhältnis der tatsächlichen Verzweigung zur theoretisch möglichen Verzeigung läßt sich deshalb als Deskriptor verwenden. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 17 2D Deskriptoren (III) Allgemeine Definitionen: Zi Ordnungszahl (H=1, C=6, LP=0) hi Anzahl H-Atome die an Atom i gebunden sind di Anzahl schwerer Atome die an Atom i gebunden sind Deskriptoren für den Verzweigungsgrad und die Flexibilität eines Moleküls: Kier & Hall Connectivity Indices pi Anzahl der s und p Valenzelektronen an Atom i vi = (pi – hi ) / (Zi – pi – 1) für alle schweren Atome 6. Vorlesung Modern Methods in Drug Discovery WS04/05 18 Kier und Hall Connectivity Indices Zi Ordnungszahl (H=1, C=6, LP=0) di Anzahl schwerer Atome die an Atom i gebunden sind pi Anzahl der s und p Valenzelektronen an Atom i vi = (pi – hi ) / (Zi – pi – 1) für alle schweren Atome 1 Chi0 0. Ordnung 0 d für alle Schweratom e mit di 0 i i Chi1 1. Ordnung 1 j i i 1 di d j für alle Schweratom e wenn i an j gebunden ist Chi0v Valenzindex 6. Vorlesung 0v i 1 vi für alle Schweratom e mit vi 0 Modern Methods in Drug Discovery WS04/05 19 Kier und Hall Shape Indices (I) n Anzahl schwerer Atome (Nicht-Wasserstoffatome) m Anzahl aller Bindungen zwischen den schweren Atomen p2 Anzahl der Pfade mit Länge 2 p3 Anzahl der Pfade mit Länge 3 Kappa1 n(n 1) 2 1 m2 Kappa2 (n 1)(n 2) 2 2 p 22 Kappa3 Kappa3 6. Vorlesung aus der Distanzmatrix D (n 1)(n 3) 2 3 für ungerade n 2 p3 (n 3)(n 2) 2 3 für gerade n 2 p3 Modern Methods in Drug Discovery WS04/05 20 Kier und Hall Shape Indices (II) Setzt man die Atome in Relation zu sp3-hybridisierten C-Atomen so erhält man die Kappa alpha Indices ri ri Kovalenzradius von Atom i 3 r Kovalenzradius eines sp r 1 c i c Kohlenstoffatoms n KappaA1 1 s ( s 1) 2 mit s n 2 (m ) Element Hybridisierung C sp3 0 C sp2 -0.13 C sp -0.22 N sp3 -0.04 N sp2 -0.20 N sp -0.29 O sp3 -0.04 P sp3 +0.43 S sp3 +0.35 Cl 6. Vorlesung Modern Methods in Drug Discovery WS04/05 +0.29 21 Balaban, Wiener und Zagreb Indices n Anzahl schwerer Atome (Nicht-Wasserstoffatome) m Anzahl aller Bindungen zwischen den schweren Atomen di Anzahl schwerer Atome die an Atom i gebunden sind wi Dij Summe der nichtdiagonalen Matrixelemente von Atom i in der Distanzmatrix D i j m m n 1 BalabanJ m 1 wi w j n WienerJ (Pfad Nummer) 1 2 wi i n WienerPolarität 1 2 w i Korreliert mit den Siedepunkten von Alkanen wenn Dij 3 i Zagreb d 2 i für alle schweren Atome i i 6. Vorlesung Modern Methods in Drug Discovery WS04/05 22 Was sagen die topologischen Indices aus ? Topologische Indices sind assoziert mit Verzweigunsgrad des Moleküls Größe und räumliche Ausdehnung des Moleküls Strukturelle Flexibilität In der Regel läßt sich eine chemische Eigenschaft nicht direkt mit einem einzigen Index korrellieren. Topologische Indices kodieren prinzipiell dieselben Eigenschaften wie fingerprints, jedoch weniger einleuchtend aber numerisch einfacher aufzustellen 6. Vorlesung Modern Methods in Drug Discovery WS04/05 23 3D Deskriptoren Bei Deskriptoren die Atomkoordinaten des Moleküls verwenden spricht man von 3D Deskriptoren. Diese sind deshalb in der Regel konformationsabhängig. Beispiele: Van der Waals Volumen, Molekulare Oberfläche, Polare Oberfläche, Elektrostatisches Potential (ESP) 6. Vorlesung Modern Methods in Drug Discovery WS04/05 24 Quantenmechanische Deskriptoren (Auswahl) Atomladungen (partial atomic charges) Keine Observablen ! Mulliken Populationsanalyse Electrostatic potential (ESP) derived charges E Dipolmoment Polarisierbarkeit LUMO HOMO HOMO / LUMO (eV) der Grenzorbitale WienerJEnergien (Pfad Nummer) Covalent hydrogen bond acidity/basicity Donor Differenz der HOMO/LUMO Energien zu Wasser Akzeptor Lit: M. Karelson et al. Chem.Rev. 96 (1996) 1027 6. Vorlesung Modern Methods in Drug Discovery WS04/05 25 DRAGON Programm zur Erzeugung von >1400 Deskriptoren BalabanJ WienerJ (Pfad Nummer) WienerPolarität Roberto Todeschini Zagreb Siehe: http://www.disat.unimib.it/chm/Dragon.htm 6. Vorlesung Modern Methods in Drug Discovery WS04/05 26 Weiterführende Information zu Deskriptoren Roberto Todeschini, Viviana Consonni Handbook of Molecular Descriptors, Wiley-VCH, (2000) 667 Seiten (ca. 270 €) BalabanJ WienerJ (Pfad Nummer) CODESSA Alan R. Katritzky, Mati Karelson et al. http://www.codessa-pro.com WienerPolarität MOLGEN C. Rücker et al. http://www.mathe2.uni-bayreuth.de/molgenqspr/index.html Zagreb 6. Vorlesung Modern Methods in Drug Discovery WS04/05 27 Smilaritätsdeskriptoren und Indices (I) A erfüllte Eigenschaft von Molekül A |A B| Schnittmenge gemeinsamer Eigenschaften von A und B |A B| Vereinigunsmenge der Eigenschaften von A und B Euklidische Distanz Manhattan Distanz B B A Formel D A, B A N 2 x x iA iB N D A, B xiA xiB i 1 i 1 DA, B A B A B Definition DA, B A B A B Bereich Andere Namen ∞ bis 0 - 6. Vorlesung Modern Methods in Drug Discovery WS04/05 ∞ bis 0 City-Block, Hamming 28 Smilaritätsdeskriptoren und Indices (II) Soergel Distanz Tanimoto Index D A, B xiA xiB / max( xiA , xiB ) S A, B N N N N 2 2 xiA xiB / xiA xiB xiA xiB i 1 i 1 i 1 i 1 DA, B A B A B / A B S A, B A B / A B N N i 1 i 1 1 bis 0 -0.333 bis +1 (kontinuierliche Werte) 0 bis +1 (binäre on/off Werte) - Jaccard Koeffizient Bei binären (dichotomen) Werten sind Soergel Distanz und Tanimoto Index zueinander komplementär 6. Vorlesung Modern Methods in Drug Discovery WS04/05 29 Smilaritätsdeskriptoren und Indices (III) Dice Koeffizient S A, B Cosinus Koeffizient N N N N 2 2 2 xiA xiB / xiA xiB S A, B xiA xiB / i 1 i 1 i 1 i 1 S A, B 2 A B / A B -1 bis +1 0 bis +1 N x x i 1 2 iA i 1 2 iB S A, B A B / A B 0 bis +1 (kontinuierliche Werte) 0 bis +1 (binäre on/off Werte) Hodgkin Index Czekanowski Koeffizient Sørensen Koeffizient Monoton mit dem Tanimoto Index 6. Vorlesung N Carbo Index Ochiai Koeffizient Hoch korreliert mit dem Tanimoto Index Modern Methods in Drug Discovery WS04/05 30 Korrelation der Deskriptoren (I) Ebenso wie konkrete Moleküleigenschaften sind auch die Deskriptoren n oft miteinander korreliert. x x y y r y Korrelation nach Pearson i 1 i i 2 2 xi x yi y i 1 i 1 n x hoher Korrelationsgrad r > 0.84 geringer Korrelationsgrad 0< r < 0.84 r < 0.5 anti-korreliert n [1...1] Auftragung zweier Variablen x und y im Craig-Plot Um aus der Vielzahl der Deskriptoren eine möglichst aussagekräftige Kombination zu erhalten, müssen multivariante Methoden der Statistik angewandt werden. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 31 Korrelation der Deskriptoren (II) Im allgemeinen hat steht man vor dem Problem aus der Vielzahl vorhandener Deskriptoren die statistisch relevanten (und damit die aussagekräftigsten) für die jeweilige QSARGleichung zu finden. Pro Deskriptor sollten 5 Moleküle (Datenpunkte) vorhanden sein, sonst ist die Gefahr einer zufälligen Korrelation zu hoch Lösungsansatz: Ermittlung der unkorrelierten Variablen mittels einer principal component analysis (PCA) – siehe unten – oder Anwendung der partial least square (PLS) Technik 6. Vorlesung Modern Methods in Drug Discovery WS04/05 32 Partial least square (PLS) Die Aktivität y wird als spezielle Linearkombination der Variablen bzw. Moleküleigenschaften xi ausgedrückt y b1 t1 b2 t2 b3 t3 bm tm wobei t1 c11 x1 c12 x2 c1n xn t 2 c21 x1 c22 x2 c2 n xn t m cm1 x1 cm 2 x2 cmn xn Die latenten Variablen ti werden so konstruiert, daß sie zueinander orthogonal, also unkorreliert sind. → Statistikprogramme D.h. durch Kombination der ursprünglichen Moleküleigenschaften werden neue Komponenten erzeugt, die unkorreliert zueinander sind. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 33 Principal Component Analysis PCA (I) Problem: Welche sind die entscheidenden Deskriptoren im Datensatz ? Die Hauptkomponentenanalyse erzeugt eine Serie unkorrelierter Variablen aus einem Satz korrelierter Variablen. Dazu wird eine Koordinatentransformation der Datenmatrix durchgeführt, sodaß die erste Hauptachse (pc1) die größte Streuung (Varianz) der Datenpunkte aufweist. Die zweite (pc2) und folgende Hauptachsen stehen orthogonal zueinander und deren Komponenten sind unkorreliert zueinander. Lit: E.C. Pielou: The Interpretation of Ecological Data, Wiley, New York, 1984 6. Vorlesung Modern Methods in Drug Discovery WS04/05 34 Principal Component Analysis PCA (II) Die erste Hauptachse (pc1) weißt die größte Streuung (Varianz) der Datenpunkte auf, während die zweite (pc2) und folgende Hauptachsen orthogonal dazu stehen. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 35 Principal Component Analysis PCA (III) Die signifikanten Hauptkomponenten haben meistens einen Eigenwert >1 (Kaiser-Guttman Kriterium). Zusätzlich tritt meistens ein Knick zu den weniger relevanten auf (Scree-Test) 6. Vorlesung Modern Methods in Drug Discovery WS04/05 36 Principal Component Analysis PCA (IV) Durch die so ermittelten relevanten Hauptkomponenten sollte sich mehr als 80% der gesamten Varianz erfassen lassen 6. Vorlesung Modern Methods in Drug Discovery WS04/05 37 Principal Component Analysis (V) Bsp: Durch welche Deskriptoren wird der logP bestimmt ? Eigenschaft Dipolmoment Polarisierbarkeit Mittel des +ESP Mittel des –ESP Variance des ESP Minimales ESP Maximales ESP Molekülvolumen Oberfläche Anteil an der Gesamtvariance pc1 0.353 pc2 pc3 0.504 0.397 -0.175 0.151 -0.389 0.104 0.160 0.403 -0.244 -0.239 -0.149 0.548 0.422 0.170 0.506 0.106 0.519 0.115 28% 22% 10% Lit: T.Clark et al. J.Mol.Model. 3 (1997) 142 6. Vorlesung Modern Methods in Drug Discovery WS04/05 38 QSAR-Gleichungen (I) Hat man nun möglichst viele unkorrelierte Eigenschaften, müßen nun noch die Koeffizienten ki bestimmt werden. Dies geschieht durch multiple lineare Regressionsanalyse (least square fit der besten Kombination der Koeffizienten) → Statistikprogramme Meistens kann man nicht die beste Kombination aller möglichen Kombinationen von Deskriptoren berechnen. (exponentielle Laufzeit) In der Regel fängt man deshalb mit dem Deskriptor an der die höchste Einzelkorrelation zeigt und nimmt schrittweise weitere Deskriptoren hinzu (forward regression). Oder man fängt mit allen Deskriptoren an und entfernt sukzessive diejenigen die die Korrelation am wenigsten verschlechtern (backward regression). 6. Vorlesung Modern Methods in Drug Discovery WS04/05 39 QSAR-Gleichungen (II) Die wichtigsten Statistischen Größen zur Beurteilung einer QSAR-Gleichung sind: Korrelationskoeffizient (quadriert als r2) Standartabweichung (standard deviation, se, möglichst klein, se<0.4 Einheiten) Fisher value F (Maß für die Übertragbarkeit der QSARGleichung auf einen anderen Datensatz, sollte möglichst hoch sein, wird aber mit zunehmender Anzahl der Variablen kleiner) Probability value p einer einzelner Variablen (Maß für zufällige Korrelation, p<0.05 = 95% Sicherheit) 6. Vorlesung Modern Methods in Drug Discovery WS04/05 40 QSAR-Gleichungen (III) Zur Überprüfung der Aussagekraft der QSAR-Gleichung werden vor allem zwei gebräuchliche Möglichkeiten verwendet: a) willkürliche Vertauschung der tatsächlichen Aktivitäten (falscher Datensatz) sollte die Voraussagefähigkeit (Standardabweichung) der Gleichung zusammenbrechen lassen. b) Cross-validation Es werden verschiedene Gleichungen aufgestellt, wobei jeweils eine Klasse von Eigenschaften (Physicochemisch, biologisch, elektronisch, sterisch) weggelassen wird (leave-one-out) und das Ergebnis mit dem vollständigen Modell verglichen wird. Die erhaltene Standardabweichung wird als PRESS (predictive residual sum of squares) bezeichnet. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 41 QSAR-Gleichungen (IV) Cross-validation Der Korrelationskoeffizient q2 der aus der cross-validation erhalten wird ist kleiner als der ursprüngliche Wert r2, aber entsprechend aussagekräftiger. Einer der besten Tests ist jedoch die Überprüfung mit einem externen Datensatz. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 42 Interpretation von QSAR-Gleichungen (I) Die Art der enthaltenden Variablen bzw. Deskriptoren sollte Rückschlüße auf die zugrunde liegenden physiko-chemischen Vorgänge zulassen und so das Design neuer Moleküle durch Interpolation ermöglichen Die mathematische Form der QSAR-Gleichung kann Aufschluß über den biologischen Wirkungsmechanismus geben: Eine Abhängigkeit der Aktivität von (log P)2 deutet auf einen Transportvorgang des Wirkstoffes zum Rezeptor hin. Vorsicht ist bei der Extrapolation über die Grenzen des erfaßten Datenbereiches angebracht. Hier können keine zuverlässigen Vorhersagen gemacht werden. 6. Vorlesung Modern Methods in Drug Discovery WS04/05 43 Interpretation von QSAR-Gleichungen (II) Zwischen den verwendeten Deskriptoren und der Meßgröße sollte ein schlüssiger Zusammenhang stehen. Hierzu ein Gegenbeispiel: H. Sies Nature 332 (1988) 495. Wissenschaftlicher Beweis, daß der Storch die Babies bringt 2100 1900 storks babies 1700 amount 1500 1300 1100 900 700 500 1965 1967 1969 1971 1973 1975 1977 1979 1981 year Die Daten hierzu finden sie unter /home/stud/mihu004/qsar/storks.spc 6. Vorlesung Modern Methods in Drug Discovery WS04/05 44