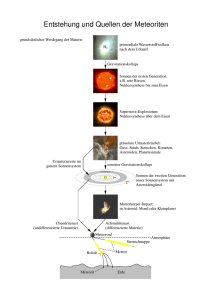
PowerPoint-Präsentation

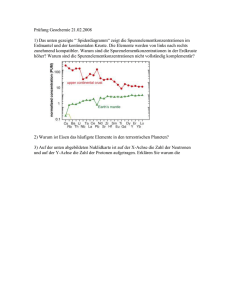
NUKLEOSYNTHESE
Die Entstehung der Elemente im Universum
Florian Folger
Betreuer: Prof. Dr. Ulrich Heber
Astrophysikalisches Seminar WS 2006/07
Woher kommen diese Elemente?
Woher kommen diese Elemente?
NUKLEOSYNTHESE
1.
2.
3.
4.
Im frühen Universum
In Sternen
Im interstellaren Medium
Durch Neutroneneinfang
5. Anwendung: Das
Alter des Universums
1. Nukleosynthese im frühen Universum
Elementbildung
beginnt nach ca. 200s
mit Deuterium und
Helium
http://www.astro.ucla.edu/~wright/BBNS_vs_t.gif
 mc 2 
nn

 exp 
np
kT 

Bis dahin stehen
alle existierenden
Teilchen miteinander
im thermischen
Gleichgewicht.
(Neutronen, Protonen,
Elektronen, Positronen,
Photonen & Neutrinos)
1. Nukleosynthese im frühen Universum
Beim Einsetzen der Elementbildung beträgt das
Neutron/Proton Verhältnis etwa 0.14.
Fast alle freien Neutronen werden für 4HeSynthese verbraucht
nn
n 4 He 

n( H ) 2n p  nn 
bzw.
2nn
Y

X n p  nn 
Mit Y + X = 1 (Massenanteile) erhalten wir für
Y = 0,25 was durch Untersuchungen an sehr alten
planetarischen Nebeln bestätigt wurde.
1. Nukleosynthese im frühen Universum
http://imagine.gsfc.nasa.gov/Images/teachers/
posters/elements/booklet/energy_big.jpg
1. Nukleosynthese im frühen Universum
Elemente jenseits von A = 8 können hier nicht
erzeugt werden.
Bei A = 5 (8)
existiert kein
stabiles Nuklid
Schwerere
Elemente werden
In Sternen bei
höheren Dichten
gebildet.
http://www.physics.ohio-state.edu/~phillips/bang/network.gif
1. Nukleosynthese im frühen Universum
http://www.astro.ucla.edu/~wright/BBNS_vs_t.gif
Woher kommen diese Elemente?
http://astro.physik.tu-berlin.de/~sonja/Materiekreislauf/matkr.gif
Der Materiekreislauf
2. Nukleosynthese in Sternen
2. Nukleosynthese in Sternen
Wasserstoffbrennen (pp-Kette)
Unsöld / Baschek – Der neue Kosmos (7.Auflage) S.284
Zündet ab einer Temperatur von
713
Brenndauer: t  10 a
T  5 106 K
Erzeugt wieder 4He.
Die zwischendurch erzeugten Isotope von Be,
Li und B werden in der Kette wieder vernichtet.
2. Nukleosynthese in Sternen
CNO-Zyklus
Fusioniert effizienter
4H zu 4He
Voraussetzungen:
Vorhandensein von
C, N, O als
Katalysatoren und
T  2  107 K
http://home.case.edu/~sjr16/media/cno_cycle.jpg
14
15
Die Reaktion N ( p,  ) O ist die langsamste.
Nach genügend langer Zeit wird 14N auf Kosten
von C und O angereichert.
2. Nukleosynthese in Sternen
Heliumbrennen
T  2 108 K
t  106 a
He( , )8 Be( , )12 C* 12 C  
Triple--Prozess
4
-Einfänge
12
C ( , )16 O( , )20 Ne....
Aber:
Die Sauerstoff-Reaktion ist sehr langsam, so
dass weitere Einfänge kaum noch auftreten!
Das Heliumbrennen erzeugt im Wesentlichen
12C, 16O, 20Ne und 24Mg
2. Nukleosynthese in Sternen
Kohlenstoffbrennen
T  6 108 K
12
t  300a
C  12 C 24 Mg* 20 Ne  
20Ne
Neonbrennen
T  1,5  10 9 K
20
t  1a
Ne( , )24 Mg( , )28 Si
Durch -Einfänge auf 20Ne wird 24Mg und 28Si
gebildet. Durch Nebenprozesse entsteht auch 16O.
2. Nukleosynthese in Sternen
Sauerstoffbrennen
t  0,4a
T  2 109 K
16
O  16 O  32 S  
32S, 31P, 28Si,
 31 P  p
40Ar
 28 Si  
Siliziumbrennen
T  3,5  109 K
28
t  1d
Si  28 Si  56 Ni  
56
Ni  56 Fe  2e   2e
56Fe
(-Einfang)
Woher kommen diese Elemente?
2. Nukleosynthese in Sternen
Photodesintegration
T  2 109 K
Ab einer Temperatur von etwa
haben Photonen genügend Energie um Kerne zu
zerlegen (-Teilchen abzusprengen)
31
P    35Cl
Cl    31P  
35
Die Reaktionen bilden eine lange Kette von
aufeinanderfolgenden Prozessen, die gegenseitig
im Gleichgewicht stehen.
31
P    35Cl    39K    43Sc  ...
2. Nukleosynthese in Sternen
Die Elemente bis zum Eisen
Zusätzlich zum -Einfang und Photodesintegration
gibt es unzählige Reaktionen und Gleichgewichtsreaktionen, die nun gleichzeitig ablaufen.
Zusammen mit dem s-Prozess erzeugen diese
alle Elemente von Kohlenstoff bis zur Eisengruppe.
Die Reaktionen enden beim Eisen, so dass dieses
häufiger auftritt als seine leichteren Nachbarn.
Das meiste Eisen wird jedoch in Typ I Supernovae
erzeugt.
Woher kommen diese Elemente?
Cowley - Cosmochemistry S. 204
3. Synthese im interstellaren Medium
Lithium, Beryllium
und Bor treten in
galaktischer Strahlung
um das bis zu 106fache häufiger auf
als in Sternen!
In Sternen und während
des Urknalls können
diese Elemente wegen
des „Flaschenhalses“
nicht gebildet werden.
3. Synthese im interstellaren Medium
Spallation:
Zertrümmerung schwerer Kerne durch hochenergetische Teilchen (Protonen, etc...)
Im interstellaren Medium werden C-, N- und OKerne durch Protonen zertrümmert, wobei Li, Be
und B erzeugt wird.
Die Wirkungsquerschnitte für diese Reaktionen
können in Beschleunigern bis etwa 103 GeV
bestimmt werden und liegen im Bereich der
geometrischen Kernausdehnungen.
3. Synthese im interstellaren Medium
Kann mit Hilfe der Spallation überhaupt ein so
(relativ) häufiges Vorkommen erklärt werden?
Annahmen:

PROTON

SPALL .
 1 / cm 3
 20  10  27 cm 2
Schwellenenergie für Spallation:
Kollisionsfrequenz:
E  20 MeV
vrel  0,2c
f  PROTON  SPALL .  vrel  3,78 / 109 a
Aus Häufigkeitsverteilung:
nLiBeB / nCNO  0,1
Zeit bis zu dieser Anreicherung: t  0,1 / f  2,6  107 a
Woher kommen diese Elemente?
4. Neutroneneinfang
s-Prozess in AGB-Sternen (slow-process)
Neutronen können als ungeladene Teilchen die
Coulomb-Barriere der Kerne leicht überwinden
und sich anlagern.
s-Prozess verläuft langsam gegenüber dem
konkurrierenden bZerfall, d.h. vereinfacht:
Wann immer ein bZerfall auftreten kann,
so tut er dies auch.
Dieser Prozess folgt einem wohldefinierten Pfad.
4. Neutroneneinfang
Cowley - Cosmochemistry S.215
4. Neutroneneinfang
EAS Publication Series 7 (2003) S. 180
s-Prozess findet statt, sobald Neutronen
vorhanden sind. Dabei gilt jedoch N n  1011 cm 3
Vereinfacht: Jedes Nuklid hat einen eindeutigen
Nachfolger. dN
i
  N n N i  i i 1v  N n N i 1  i 1i v
dt
v
Relativgeschwindigkeit
Neutron/Nuklid

Wirkungsquerschnitt
4. Neutroneneinfang
Woher kommen die Neutronen?
13

13
16






C
p
,

N
,
e

C

,
n
O
•
e
benötigt 12C aus He-Kern und
Protonen aus H-Brennschale.
12
•
N  ,18 F , e  e 18O ,  22 Ne , n25 Mg
benötigt C,N,O aus He-Brennschale und
14N aus CNO-Zyklus in H-Brennschale.
Erzeugt währende He-Flash kurzzeitig Neutronen.
14
Durchmischung der einzelnen Schichten
ist für Neutronenproduktion notwendig!
4. Neutroneneinfang
r-Prozess in Typ II Supernovae (rapid-process)
Elemente jenseits des -stabilen 83Bi können durch
den s-Prozess nicht erzeugt werden.
r-Prozess benötigt noch höhere Neutronendichten,
wie sie in Supernovae auftreten. N  3  1025 cm  3
n
Er erzeugt neutronenreiche Nuklide, da er schnell
gegenüber dem konkurrierenden bZerfall abläuft.
Neutronen kommen aus der Neutralisierung von p:
p  e  n  e
4. Neutroneneinfang
Cowley - Cosmochemistry S.215
4. Neutroneneinfang
Cowley - Cosmochemistry S.223
4. Neutroneneinfang
Der r-Prozess folgt keinem wohldefinierten Pfad.
Neutronen werden angelagert, bis ein Gleichgewicht
zwischen der n, und der ,nReaktion vorliegt.
Unter der Annahme, dieser GG-Punkt sei wohl
definiert, gilt: dN
Z

  Z 1 N Z 1   Z N Z
b-Zerfallsdt
rate
Probleme:
• GG-Punkt ist verschmiert.
• Was passiert, wenn alle Neutronen aufgebraucht
sind?
4. Neutroneneinfang
p-Prozess
Anlagerung von Protonen erzeugt die protonenreichen Nuklide.
Dies ist ein sekundärer Prozess, der auf Nukliden
aufbaut, die bereits durch s- oder r-Prozess erzeugt
wurden.
Aufgrund der zu überwindenden Coulombbarriere
sind die Raten etwa um eine Größenordnung
niedriger. Die Herkunft der freien Protonen ist
noch ungeklärt.
Cowley - Cosmochemistry S.225
4. Neutroneneinfang
Produktion der Elemente schwerer als Fe
Alle drei Prozesse
haben Maxima bei
Kernen mit „vollen“
Kernschalen.
Offene Frage:
Wieso erzeugen sund r-Prozess die
gleichen Häufigkeiten,
obwohl sie unabhängig voneinander
ablaufen?
Zusammenfassung
5. Das Alter des Universums
Altersbestimmung anhand von 238U analog zur
14C-Methode.
TH  4,47  109 a
238U
ist das seltenste Element und kann nur in
sehr alten metallarmen Sternen gemessen werden.
238U
wird im gleichen Prozess erzeugt (r-Prozess),
wie seine stabilen Nachbarn. (Hier Os) Diese alten
Sterne haben die gleichen Metallverteilungen wie
unsere Sonne jedoch nur mit 12% der solaren
Häufigkeit.
238U ist allerdings nur zu 6% vorhanden.
Alter aus dem Verhältnis 238U / Os
5. Das Alter des Universums
www.eso.org/outreach/press-rel/pr-2001/pr-02-01.html
www.eso.org/outreach/press-rel/pr-2001/pr-02-01.html
5. Das Alter des Universums
Synthetische Spektren für
fest angenommene
Häufigkeiten der stabilen
Elemente und 4 variablen
Häufigkeiten von 238U.
Die rote Kurve reproduziert
die Messdaten „am Besten“.
Diese gehört zu einer 238UHäufigkeit von 6% der der
Sonne.
5. Das Alter des Universums
238



U / Os 0 bei der Bildung
Das Verhältnis 0
eines Sterns folgt aus Modellrechnungen, die
beachten, dass sich das Verhältnis der stabilen
r-Prozess-Elemente mit der Zeit nicht ändert.
Mit Hilfe des radioaktiven Zerfallsgesetzes
kann das Alter des Sterns bestimmt werden.
 ln 2 
t
 TH 
 t    0 exp 
t Stern  (12,5  1,5)  109 a
Das Universum ist mindestens
12,5·109 Jahre alt.
Literatur
Unsöld / Baschek – Der neue Kosmos (7.Auflage)
Springer-Verlag 2005
Cowley – Cosmochemistry (Chapter 10: Energy Generation in stars
and Nucleosynthesis) ???
Knödleder – Supernova Nucleosynthesis
EAS Publication Series, 7 (2003) 177 – 215
Herwig – Evolution of Asymptotic Giant Branch Stars
Annu. Rev. Astron. Astrophys. 2005. 43:435 – 79
How old is the universe?
ESO Press Release 02/01
www.eso.org/outreach/press-rel/pr-2001/pr-02-01.html
Cayrel / Hill et al. - Measurement of stellar age from uranium decay
Nature Vol. 409 S. 691 - 692