(const tbVector3& v) { return tbMatrix (1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f

Softwaretechnologie II (Teil 1):
Simulation und 3D Programmierung
Manfred Thaller
WS 2012/2013
3D-Grafik: Mathe
Linda Scholz
Was ist 3D Grafik?

Vektoren

Matrizen

Aufbau Direct3D – Zuständigkeitsbereich
Schnittstellen

Ebenen

Farbgebung
Zweidimensionales kartesisches
Koordinatensystem
Dreidimensionales kartesisches
Koordinatensystem
Darstellung dreidimensionaler
Objekte

Abbildung auf dem Bildschirm
durch Projektion


Bildtiefe wird vermittelt
Einsatz von Polygongrafik



Verbindung von Bildpunkten zu
mehreren Dreiecken
Annährung an den „perfekten“ Körper
Durchschnittliche Größenordnung zur Annährung
liegt bei 10.000 Polygonen
Vektoren

Positionsvektoren


Richtungsvektor



Koordinaten eines Punktes
Gibt Bewegungsrichtung an
In Kombination mit der Geschwindigkeit auch
Bewegungsvektoren genannt
Vektorkomponenten vom Blickwinkel des
Betrachters abhängig
Rechenoperationen


Grundrechenarten zur Bewegung,
Verlängerung oder Stauchung
Punktprodukt / Skalarprodukt


Bestimmt Kosinus eines Winkel zwischen zwei
Richtungsvektoren
Kreuzprodukt

Steht senkrecht auf den
Vektoren aus denen es
gebildet wurde
Rechenoperationen

Länge eines Vektors / Distanz zwischen zwei
Punkten


Berechnung durch Satz des Pythagoras
Normalisierte Vektoren (Richtungsvektoren)

Länge 1 – pure Richtungsangabe

Bewegungsvektor wird durch seine Länge geteilt

Verhindert unerwartete Werte

Wichtig bei Berechnung des Punktprodukts
Programmierung einer Vektorklasse

Implementierte Klasse : tbVector3

TBVECTOR3.H


TBVECTOR3.CPP


Deklaration und Inline-Methoden
Definition / Implementierung
Variablen

Drei float Variablen für die Komponenten x, y, z
Konstruktoren

Standardkonstruktor

Kopierkonstruktor


Erwartet Referenz auf ein anderes tbVector3-Objekt

Kopiert den angegeben Vektor
Konstruktor

Setzt Vektorkomponenten ein
Operatoren


Arithmetische Operatoren lassen sich
komponentenweise durchführen
Bsp:
inline tbVector3 operator * (const tbVector3& a,
const tbVector3& b)
{
return tbVector3(a.x * b.x, a.y * b.y, a.z * b.z);
}
Operatoren

Zuweisungsoperatoren


Werden innerhalb der Klasse definiert
Vergleichsoperatoren

Überprüfung zur Gleichheit bzw. Ungleichheit
zweier Vektoren
D3DVECTOR

Struktur zur Darstellung von Vektoren

Wird von Direct3D verwendet

Identisch mit tbVector3

Verbindung zur tbVector3 Klasse durch Casting
operator D3DVECTOR& ()
{
return *((D3DVECTOR*)(this));
}
3D Spieleprogrammierung Seite 56
Hilfsfunktionen

Vektorlänge und Quadrat der Vektorlänge

tbVector3Length

tbVector3LengthSq
inline float tbVector3Length(const tbVector3& v)
{
return sqrtf(v.x * v.x + v.y * v.y + v.z * v.z);
}
Hilfsfunktionen

Normalisieren eines Vektors

tbVector3Normalize

Teilt Vektor durch seine Länge
inline tbVector3NormalizeEX(const tbVector3& v)
{
return v / (sqrtf(v.x * v.x + v.y * v.y + v.z * v.z) + 0.0001f);
}
Wenn man nicht sicher ist ob der Vektor die Länge null hat,
erreicht man durch Addition eines Kontrollwerts „sicheres“
Normalisieren
Hilfsfunktionen

Das Kreuzprodukt

tbVector3Cross
inline tbVector3 tbVectorCross(const tbVector3& a,
const tbVector3& b)
{
return tbVector3(a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x);
}
Hilfsfunktionen

Punktprodukt

tbVector3Dot (berechnet lediglich Punktprodukt)

tbVector3Angle rechnet Kosinuswert zusätzlich um
Seite 59
inline float tbVector3Angle(const tbVector3& a,
const tbVector3& b)
{
return acosf((a.x * b.x + a.y * b.y + a.z * b.z) /
sqrtf((a.x * a.x + a.y * a.y + a.z * a.z) *
(b.x * b.x + b.y * b.y + b.z * b.z)));
}
//Punktprodukt
//Vektorlänge
Hilfsfunktionen

Minimum- und Maximumvektoren



Geben Minimum- bzw. Maximumvektor mehrerer
Vektoren an
tbVector3Min bzw. tbVector3Max
Zufallsvektoren

Liefert zufälligen normalisierten Vektor

tbVector3Random

Funktion für die Richtung : tbFloatRandom

Einsatz für Explosionen, Rauch, etc.
Hilfsfunktionen

Lineare Interpolation

Positionsbestimmung eines Objekts zu einer
gewissen Zeit

Start- und Zielpunkt sind bekannt

tbVector3InterpolateCoords



Seite 61
Interpoliert man Normalenvektoren ist das Ergebnis
nicht gleichzeitig auch ein Normalenvektor
tbVector3InterpolateNormale (Interpoliert und
normalisiert)
tbVector3InterpolateNormalizeEx (Interpoliert,
normalisiert und prüft ob Vektor die Länge null hat)
Hilfsfunktionen
inline tbVector3 tbVector3InterpolateNormal(const tbVector3& a,
const tbVector3& b,
const float s)
{
return tbVector3NormalizeEx(a + s * (b – a));
}
Hilfsfunktionen

Zur Überprüfung ist es hilfreich, wenn man
Vektoren ins Logbuch schreibt



tbWriteVector3ToLog
Übersicht der Hilfsfunktionen für Vektoren und
Beispielcode auf Seite 63
Für die Arbeit mit 2D-Vektoren gibt es die
Klasse tbVector2 mit 2D Funktion ähnlich zu
den gerade kennengelernten
Matrizen



Matrix = rechteckige
Anordnung von Zahlen
Verschiedene Menge
Zeilen und Spalten
Identitätsmatrix
Verkörpert das neutrale Element
Rechenoperationen
Multiplikation von Matrizen

Spaltenanzahl
von Matrize A
muss mit
Zeilenanzahl
von Matrize B
identisch sein
Matrizen dividieren



Division durch Multiplikation mit dem Kehrwert
Kehrwert ist das inverse Element – bei einer
Matrix muss es die Identitätsmatrix ergeben
Invertierte Matrix bringt man durch Exponenten
-1 zum Ausdruck
Transformationen

Verschiebung

Rotation

Skalierung


Man betrachtet Vektoren als Matrix mit Zeilen
und Spalten
Man geht von absoluten Koordinaten mit dem
Objektmittelpunkt (0, 0, 0) aus
Transformationsmatrix



Transformationsmatrix verwendet 4 Spalten und
4 Zeilen
Verbleibende Zeile
füllt man mit einer 1
(w Koordinate)
Resultierende
w Koordinate muss 1 sein. Ist dies nicht der Fall
teilt man alle Komponenten durch sie
Transformationen

Translationsmatrix

Verschiebt einen Vektor

Simple Vektoraddition

Xp = xm*C11 + ym*C21 + zm*C31 + C41

Matrixelement C41 fließt „nur“ durch Addition ein

Bei Yp C42 und bei Zp C43

Füllt man diese Elemente (innerhalb einer
Identitätsmatrix) aus, wird eine Translation
durchgeführt
Transformation

Skalierungsmatrix

Skalierung bedeutet Multiplikation eines Vektors

Man nutzt die Identitätsmatrix

Xo = x*Sx + y*0 + z*0 + 0

Es finden lediglich Multiplikationen der
einzelnen Komponenten statt
Transformationen

Rotationsmatrizen

Gleichung zur Drehung eines Punktes um den
Koordinatenursprung:



x = (x * cos α) + (y * (- sin α))
y = (x * sin α) + (y * cos α)
Dieses Verfahren kann man auf die Rechnung mit
der Matrix anwenden
Es muss beachtet werden, welche Komponenten
angesprochen werden
Transformationen von
Richtungsvektoren


Können nicht verschoben werden (haben keine
Position, beschreiben lediglich eine Richtung)
Bei einer Transformation müssen die m und n
Werte vertauscht werden
(transformierte invertierte
Transformationsmatrix)
Transformationen


Man kann innerhalb einer Matrix mehrere
Funktionen (Translation, Skalierung, Rotation)
vieler Matrizen vereinen
Reihenfolge ist wichtig

Skalierung

Rotation

Translation
Matrix als Koordinatensystem


Um eine Matrix zu erhalten die einen Punkt in
ein anderes Koordinatensystem umrechnet,
muss eine Translation um den Ursprung
stattfinden
Um Koordinatensystemmatrix zu erhalten muss
man Rotationsmatrix mit Translationsmatrix
multiplizieren
Projektionsmatrix


Projektion eines dreidimensionalen Vektors auf
eine Ebene (Bildschirm)
Dreiecke die vor oder hinter einer gewissen
Ebene (nahe und ferne Clipping-Ebene) werden
nicht mehr dargestellt

Entfernung der Clipping Ebene

Blickfeld des Betrachters

Seitenverhältnisse des Bildes
Projektionsmatrix

Projektionsmatrize bestimmt das Sichtfeld des
Betrachters
Sichtfelder – Clipping Ebenen
Kameramatrix

Virtueller Beobachter lässt sich in 3D Szene
einfügen





Position und Ausrichtung muss bekannt sein
- Blickpunkt der Kamera
Nach-oben-Vektor –Kamerabewegung
Dreht man Kamera nach links werden
Objektvektoren nach rechts bewegt
Man wendet Kameramatrix vor Projektions- und
nach Transformationsmatrizen an
beinhaltet eigenes Koordinatensystem
Implementierung
• Variablen der Klasse tbMatrix
• 16 float Variablen (m11 bis m44)
• Konstruktoren
• Standardkonstruktor
• Kopierkonstruktor mit Referenz auf eine andere
Matrix. Kopiert die angegebene Matrix
• Konstruktor der die Werte der float-Parameter in die
Matrix hineinkopiert
Operatoren
• Addition und Subtraktion sind identisch zur
Vektorklasse
• Divisionsoperator invertiert rechte Matrix und
multipliziert linke damit
• tbMatrixInvert
• tbMatrixTranspose
• Multiplikation ist recht komplex
Operatoren
inline tbMatrix operator * (const tbMatrix& a,
const tbMatrix& b)
{
return tbMatrix(b.m11 * a.m11 + b.m21 * a.m12 + b.m31 * a.m13 + b.m41 * a.m14,
b.m12 * a.m11 + b.m22 * a.m12 + b.m32 * a.m13 + b.m42 * a.m14,
b.m13 * a.m11 + b.m23 * a.m12 + b.m33 * a.m13 + b.m43 * a.m14,
[…]
[…]
[…] );
}
• Es lohnt sich auf vorhandene CPU-Features
zurückzugreifen
Zugriffsoperatoren
• Zur Übergabe von Variablen benötigt man ein
zweidimensionales Array
class TRIBASE_API tbMatrix
{
public:
union
{
struct
{
float
m11, m12, m13, m14,
m21, m22, m23, m24,
m31, m32, m33, m34,
m41, m42, m43, m44;
}
float m[4] [4];
};
[…]
//Elemente der Matrix
//Zweidimensionales Array
Zugriffsoperatoren
• Durch Überladen des „()“-Operators der tbMatrixKlasse kann man Elemente einzeln ansprechen
class TRIBASE_API tbMatrix
{
public:
[…]
//Zugriffsoperatoren
float& operator () (int iRow, int iColumn) {return m[iRow - 1] [iColumn - 1];}
float operator () (int iRow, int iColumn) const {return m[iRow - 1] [iColumn - 1];}
};
tbMatrix m;
m(1, 3) = 100.0f;
m(2, 1) = -50.0f;
//Matrixelemente lassen sich einzeln verändern
float f = m(1, 2);
// zur allgemeinen Abfrage
Implementierung
• Identitätsmatrix und Translationsmatrix lassen
sich leicht erzeugen
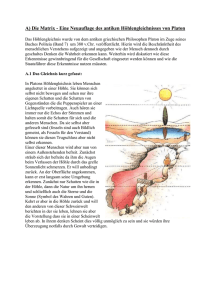
TRIBASE_API tbMatrix tbMatrixTranslation (const tbVector3& v)
{
return tbMatrix (1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
v.x, v.y, v.z, 1.0f);
• Identitätsmatrix wird durch tbMatrixIdentity
erzeugt, in dem man die ersten drei Zeichen
der letzten Zeile auf 0.0f setzt.
Implementierung
• Rotationsmatrix
• Man kann Rotation für alle Achsen separat
vornehmen Seite 79-80
• tbMatrixRotationX
• tbMatrixRotationY
• tbMatrixRotationZ
• Sinus- und Kosinuswerte müssen nur einmal
berechnet werden.
Implementierung
• Rotation um alle drei Achsen
TRIBASE_API tbMatrix tbMatrixRotation (const tbVector3& v)
{
return tbMatrixRotationZ(v.z) * tbMatrixRotationX(v.x) * tbMatrixRotationY(v.y);
}
• Rotation um eine beliebige Achse ebenfalls
möglich Seite 81
• tbMatrixRotationAxis
Implementierung
• Skalierungsmatrix
TRIBASE_API tbMatrix tbMatrixScaling (const tbVector3& v)
{
return tbMatrix(v.x, 0.0f, 0.0f, 0.0f,
0.0f, v.y, 0.0f, 0.0f,
0.0f, 0.0f, v.z, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
}
Weitere Hilfsfunktionen
• tbMatrixAxes
• Man übergibt Achsenvektoren zur Berechnung der
Achsenmatrix
• Ausgabe der Ausrichtung eines Objekts
• tbMatrixDet
• Bestimmt Determinante einer Matrix
• tbMatrixInvert
• Invertiert angegebene Matrix
• tbMatrixTranspose
• Transponiert eine Matrix
Weitere Hilfsfunktionen
• tbMatrixcamera
• Kameramatrix berechnen durch Positionsvektor
vPos, Richtungsvektor vLookAt und „Nach-ObenVektor“ vUp für Kameradrehung
• Translationsmatrix wird entgegengesetzt der
Kameraposition erzeugt
• Achsenvektoren der Kamera in eine Matrix eintragen
• Beide multiplizieren und man erhält die
Kameramatrix
• tbMatrixProjection
• Erzeugt eine Projektionsmatrix
Weitere Hilfsfunktionen
• tbVector3TransformCoords
• Positionsvektor mit Matrix multiplizieren
• W-Koordinate wird für den Fall einer Projektion
geprüft
• tbVector3TransformNormal
• Richtungsvektor mit Matrix multiplizieren
• Transponierte invertierte Matrix wird benötigt
• Transformierter Vektor soll selbe Länge wie
Originalvektor erhalten
• Hierfür wird ursprüngliche Länge gespeichert
Hilfsfunktionen

Auch die Matrix kann man ins Logbuch
schreiben



tbWriteMatrixToLog
Übersicht der Hilfsfunktionen für Matrizen und
Beispielcode auf Seite 87
Für die Transformation von 2D-Vektoren gibt es
die Funktionen tbVector2TransformNormal und
tbVector2TransformCoords
Ebenen
Ebenengleichung
• Bestimmt die Menge der Punkte aus denen eine
Ebene besteht
• Stützvektor
• Liegt in der Ebene
• Normalenvektor
• Steht senkrecht auf der Ebene
• Verbindet man einen Punkt mit dem Stützvektor
muss der Verbindungsvektor senkrecht zum
Normalenvektor stehen
Lage eines Punktes
• Durch Ebenengleichung lässt sich herausfinden
ob ein Punkt auf der Ebene liegt (Ergebnis null)
• Ist das Ergebnis positiv, liegt der Punkt auf der
Vorderseite (sichtbaren Seite) einer Ebene
• Ist das Ergebnis negativ, liegt der Punkt auf der
Rückseite (nicht sichtbaren Seite) einer Ebene
• Ergebnis der Ebenengleichung wird mit
Normalenvektor dividiert um Entfernung des
Punktes zu der Ebene herauszufinden.
Implementierung
• tbPlane
• Vier Variablen (Fließkommazahlen) a, b, c und d
• Zusätzlich eine tbVector3-Variable n
(Normalenvektor)
• Kopierkonstruktor
• Leerer Konstruktor
• Konstruktor der vier float-Werte erwartet
• Konstruktor, der tbVector3-Wert und einen floatWert erwartet
• Operatoren gibt es nicht
Hilfsfunktionen
• tbPlaneNormalize
• Normalisiert Ebenen
• tbPlaneDotNormal
• Punktprodukt aus einem Vektor und dem
Normalenvektor aus der Ebene
• tbPlaneDotCoord
• Soll Punkt in Ebenengleichung einsetzen und das
Ergebnis zurückliefern
• tbPointPlaneDistance
• Distanz eines Produkts zur Ebene
Hilfsfunktionen
• tbPlaneFromPointNormal
• Erwartet einen Punkt und einen Normalenvektor und
liefert die Ebene
• tbPlaneTransform
• Man kann auch Ebenen mit Matrizen transformieren
• tbWritePlaneToLook
• Schreibt eine Ebene in die Logbuchdatei
• Übersicht der Hilfsfunktionen und Beispielcode
auf Seite 94
RGB-Farbsystem
• Ehemalige 8-Bit Grafik erschwerte eine
ausgewogene Farbgebung
RGB-Farbsystem
• 16-Bit-Grafik
• Darstellung eines Pixels basierte auf dem RGBSystem
• 16 Bits aufgeteilt in 5 Rotanteile, 6 Grünanteile und
5 Blauanteile
• 24-Bit-Grafik gefolgt von 32-Bit-Grafik
• Bei 32 Bits bleiben 8 Bits für Farbinformationen wie
Transparenz
RGB-Farbsystem
• Die vier Komponenten betrachtet man jeweils als ein
Byte
• Bei Direct3D ist es auch möglich Fließkommazahlen
(float-Wert) für die einzelnen Farbkomponenten zu
verwendet
Implementierung
• Klasse tbColor
• Vier float-Variablen (r, g, b und a – Alpha)
• Konstruktoren:
tbColor a();
tbColor b(0.5f);
//kein Parameter
//Fließkommazahl r,g,b bekommen den Wert
tbColor c(0.0f, 1.0f, 0.0f, 0.5f);
//float-Werte
tbColor d((BYTE) (0), 255, 0, 128);
//Byte-Werte
tbColor e((DWORD) (0xFF00FF80));
//DWORD-Wert
Operatoren
• Addition ergibt additive Mischung zweier Farben
• Multiplikation
• mit positivem Wert über 1 hellt auf
• Mit positivem Wert unter 1 dunkelt ab
Casting
• Farbe in ein DWORD-Wert verwandeln
tbColor Red(1.0f, 0.0f, 0.0f);
DWORD dwRed = (DWORD) (Red);
//Casting verwenden
Red
//Konstruktor verwenden
= tbColor(dwRed);
Weitere Hilfsfunktionen
• tbColorNegate
• Berechnen des Negativs
• tbColorBrightness
• Berechnung der Helligkeit
• tbColorRandom
• Erzeugt Zufallsfarbe
Diese und weitere auf Seite 97