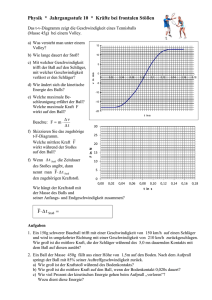
3) Luftwiderstand 4) Ursache des
Werbung

Wovon hängt die Flugbahn Fachbereich Physik Institut für Experimentalphysik eines Fussballs ab ? Arbeitsgruppe Prof. Karsten Heyne Arnimallee 14, 14195 Berlin [email protected] www.physik.fu-berlin.de/~heyne 1) Geschwindigkeit 2) Reichweite Wie schnell fliegt eigentlich ein Fußball? Dies hängt von der Geschwindigkeit, mit welcher der Fuß auf den Ball trifft und von der Impulsübertragung zwischen Fuß und Ball ab. Einfluss hierauf hat z.B. auch die Elastizität des Balls. Modell Physikalisches Pendel 1. Drehpunkt (Hüftgelenk) Modell Doppelpendel 1.Drehpunkt (Hüftgelenk) Drehung des oberen Stabs 2. Drehpunkt (Knie) Drehung des Stabs Fußpunkt Fuß In diesem Modell wird das gesamte Bein durch eine gerade Stange mit angehängtem Gewicht repräsentiert. Je höher die Anfangsauslenkung, umso grösser ist die Geschwindigkeit im tiefsten Punkt Der Drehpunkt des unteren Stabs (Knie) bewegt sich auf einer Kreisbahn, mit einer Geschwindigkeit, die sich aus der Drehgeschwindigkeit des oberen Stabs ergibt. Die dadurch hervorgerufene Zentrifugalkraft schleudert den unteren Stab nach vorn, woduch er noch schneller wird. Darum schwingt er durch und das Gelenk zwischen beiden Stäben ist beim Schuss fast gestreckt. Das untere Ende des unteren Stabs (der Fuß) ist dann ca. 3 mal so schnell wie sein Drehpunkt. In diesem Modell stellen zwei gerade Stäbe den Ober- und den Unterschenkel dar. Sie sind jeweils an ihrem oberen Ende drehbar. Nach dem Abschuss, verfolgt der Ball eine parabelförmige Flugbahn. Die Reichweite hängt nicht nur von der Anfangsgeschwindigkeit, sondern auch vom Abschusswinkel ab. Bei Vernachlässigung des Luftwiderstands fliegt der Ball am weitesten, wenn der Winkel 45° beträgt. In der Realität ist der optimale Schusswinkel wegen des Luftwiderstands kleiner als 45°(bei 100km/h harten Schüssen etwa 30°). Horizontal zurückgelegte Strecke: x u0 t Vertikal zurückgelegte Strecke: y v0 t Erot 120 km/h => Aus der Ruhelage, Ball erreicht 120 km/h 1 g t2 2 sin 0 v 0 v ges Horizontale Anfangsgeschwindigkeit: u 0 u ges cos 0 1 Q 2 Q r 2 dm 2 Aus der Ruhelage getreten, z.B. beim Elfmeterschießen, erreicht man 110-130 km/h. Wird der Ball dagegen aus dem Flug heraus angenommen, kommt noch die Hälfte der Auftreffgeschwindigkeit hinzu, so dass der Ball 150km/h schnell werden kann. 0 km/h v 2 ges v u 2 0 2 2vges sin 20 xR g Schußwinkel Theta Und die maximale Flugreichweite des Balls, bei einem Winkel von 45° lässt sich einfach ausrechnen mit: 2 0 xR,max 2 vges g Ohne Luftwiderstand wäre die Flugbahn symmetrisch, in Wirklichkeit ist Sie jedoch so geformt, dass der Ball steiler ankommt, als er geschossen wurde. Ein Ball, der idealer Weise das gegnerische Tor erreichen könnte, wird durch den Luftwiderstand in seiner Reichweite derart verringert, dass er bereits im Bereich des Mittelkreises auftrifft. 60 km/h 150 km/h => Ball trifft mit 60 km/h auf den Fuß Ball erreicht 150 km/h= (120+0,5*60)km/h 3) Luftwiderstand 4) Ursache des Luftwiderstands Die Physik fliegender Bälle !!! Der Luftwiderstand hängt von der Geschwindigkeit des Balls ab. Theoretisch wäre zu erwarten, dass mit höherer Geschwindigkeit der Luftwiderstand nahezu quadratisch zunimmt. Bei einer glatten Kugel gibt es jedoch eine kritische Geschwindigkeit von ca. 75 km/h, ab welcher der Luftwiderstand wieder abnimmt. Da die Fußballoberfläche nicht glatt ist (unter anderem wegen der Nähte), verhält er sich wiederum anders. Schon ab 30 km/h ist sein Luftwiderstand geringer als bei einer glatten Kugel, sein Luftwiderstand steigt dann jedoch mit zunehmender Geschwindigkeit langsam aber kontinuierlich an. Wie hängen Geschwindigkeit, Reichweite und Luftwiderstand zusammen? Was passiert, wenn ein Fußball angeschnitten wird? Probieren Sie es selber einmal aus und lesen Sie hier die physikalischen Grundlagen. Luftwiderstand (In Vielfachen des Ballgewichts) Ohne Luftwiderstand erhält man mit: Vertikale Anfangsgeschwindigkeit: Gesamt-Anfangsgeschwindigkeit: Allgemein gilt, je länger das Bein und je größer das Trägheitsmoment Q, desto größer die Rotationsenergie Erot umso schneller kann der Ball geschossen werden (Steiner’scher Satz). Die Flugreichweite Xr des Balls Ohne Berücksichtigung des Luftwiderstands gilt: Wirbel und Turbulenzen: Die den Ball umschließende Luftströmung wird an der Ballrückseite verzögert, so dass Wirbel entstehen. Die Bewegungsenergie der Luftwirbel wird dem Ball entzogen, der dadurch abgebremst wird. Hinter dem Ball ist die Strömung also turbulent. Bei genügend hoher Geschwindigkeit (kritischer Geschwindigkeit), wird bereits die Grenzschicht Turbulent, wodurch der Wirbelbereich hinter dem Ball kleiner wird. Dadurch ist der Luftwiderstand eines Fußballs dann verringert. Reißt ein Wirbel ab, wird eine Zirkularströmung entgegengesetzt zur Wirbelrichtung erzeugt (Drehimpulserhaltung) Die Größe des Wirbelwiderstands ist gegeben durch: Wirbelstrasse Wind: Der Luftwiderstand wirkt sich bereits bei Windstille aus. Wind kann die Flugbahn des Fußballs jedoch nochmal deutlich verändern. Die Reichweite ändert sich etwa um 1m je 1,5 km/h Gegen- oder Rückenwind. Ein Seitenwind von 45 km/h kann einen Elfmeter beispielsweise um 30 cm ablenken. Bei weiteren Distanzen kann die Ablenkung sogar einige Meter betragen. 5) Anschneiden eines Balls Eine seitlich gekrümmte Flugbahn entsteht, wenn man dem Ball einen Drall mitgibt, so dass er in der Luft (seitwärts) rotiert. Dabei ist es nicht so einfach, dennoch zielgenau zu treffen, da die Flugbahn schwer vorhersehbar ist. FW CW A v2 2 = Dichte der Flüssigkeit A = Der Strömung dargebotener Querschnitt des Körpers. Cw = Widerstand Die Widerstandszahl Cw ist abhängig von der Form des Körpers. Dabei ist vor allem dessen Rückseite wichtig, da dort die Wirbel gebildet werden. Je weniger die Körperform die Wirbelbildung fördert, um so kleiner werden Cw und Fw. Der günstigste Fall liegt vor, wenn der Körper Stromlinienform besitzt. Folgende Körper mit gleichem Querschnitt A besitzen einen Cw-Wert von: Ursache der Flugbahnkrümmung ist die asymmetrische Luftströmung um den rotierenden Ball herum. Der rotierende Ball leitet die Luftströmung zur einen Seite hin, er wird dabei selbst zur anderen Seite abgelenkt. Starker Gegenwind kann dem Ball eine sehr unerwartete Flugbahn verleihen. 24 : 20 : 8 : 6 Siehe auch POSTER 2 zum MAGNUS-EFFEKT Literatur -John Wesson: Fußball – Wissenschaft mit Kick: Von der Physik fliegender Bälle und der Statistik des Spielausgangs, 1. Auflage 2006, Elsevier Spektrum Akademischer Verlag. -M. Bormann: Experimentalphysik, Bd. 1/b, 7. Auflage 1990, Universitätsverlag Dr. N. Brockmeyer. : 2 : 1