teilchensysteme

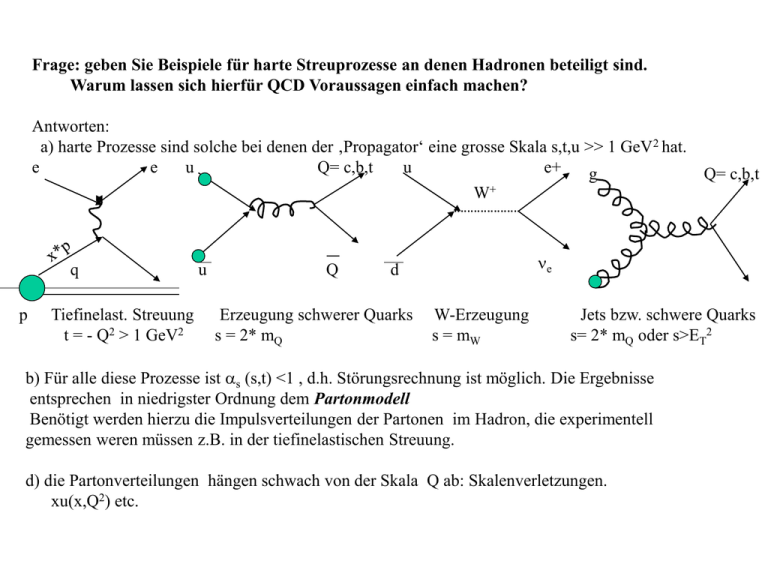
Frage: geben Sie Beispiele für harte Streuprozesse an denen Hadronen beteiligt sind.
Warum lassen sich hierfür QCD Voraussagen einfach machen?
Antworten:
a) harte Prozesse sind solche bei denen der ‚Propagator‘ eine grosse Skala s,t,u >> 1 GeV 2 hat.
e
e
u
Q= c,b,t
u
e+
g
Q= c,b,t
W+
q
p
Tiefinelast. Streuung
t = - Q2 > 1 GeV2
u
Q
ne
d
Erzeugung schwerer Quarks
s = 2* mQ
W-Erzeugung
s = mW
Jets bzw. schwere Quarks
s= 2* mQ oder s>ET2
b) Für alle diese Prozesse ist as (s,t) <1 , d.h. Störungsrechnung ist möglich. Die Ergebnisse
entsprechen in niedrigster Ordnung dem Partonmodell
Benötigt werden hierzu die Impulsverteilungen der Partonen im Hadron, die experimentell
gemessen weren müssen z.B. in der tiefinelastischen Streuung.
d) die Partonverteilungen hängen schwach von der Skala Q ab: Skalenverletzungen.
xu(x,Q2) etc.
Frage: wie unterscheiden sich elementare Bindungszustände in der
elektromagnetischen und starken Wechselwirkung (Positronium und Quarkonium)
- Wie sehen die Feynmadiagramme für das Positonium und das Charmonium aus (incl Ladungen)- Wie die zugehörigen Potentiale? Was ist gleich, was ist verschieden?
-Wann ist das Feynmandiagram für Charmonium sinnvoll, welchen Teil des Potentials beschreibt es?
- diskutieren Sie Zahl und Quantenzahlen der Bindungszustände.
Antworten:
Positronium
Charmonium
V = aem /r
V = c as /r + k*r
aem.5
as.5
g
g
aem.5
V
as.5
r
~1/r
Das Feynmandiagramm ist nur
für kleine Kopplungen sinnvoll,
wenn 1-Gluonaustausch dominiert,
d.h. bei kleinem r. das 1/r Potential
kommt von mg = 0
Bei grossem r wird as gross, es werden viele Gluonen
Ausgetauscht und die Selbstwechselwirkung der Gluonen
führt zur Ausbildung eines Farbstrings, der durch das
linear ansteigende Potential näherungsweise beschrieben wird.
Der 3. radial angeregte Zustand (n=3) liegt bereits oberhalb
der DD Schwelle  kein Bindungszustand mehr.
‚Stabile‘ Hadronen und deren Zerfaelle:
A) skizzieren Sie die Position der stabilen Baryonen mit und ohne Strangeness in einem Diagramm.
Benutzen Sie als Achsen die Flavourquantenzahlen. Geben Sie jeweils den nNamen und den Quarkinhalt an.
B) warum heissen diese Hadonen ‚stabil‘? Geben Sie jeweils dominante Zerfallskanael an. Welche
Quantenzahlen werden verletzt, welche Wechselwirkung ist verantwortlich?
C) was aendert sich wenn auch Baryonen mit Charm und Beauty betrachtet werden?
Antworten:
X-(ssd)
X0(ssu)
L
S0 (sdu)
S- (sdd)
-1
-2
-1/2
-1
1
n (ddu)
S+(suu)
1/2
p (duu)
S
1
T3
B) beim Zerfall wird jeweils eine FlavourQZ verletzt
S0-->L+g , Gesamtisospin T, el.magn.
X---> L+p- , strangeness, schw. WW.
S+--> np+ , strangeness, schw. WW.
n --> p + e +n , d-->u (Isospin), schw. WW
C) Fuer jedes u-Quark kann auch ein c-Quark eingefuegt
werden. Es gibt daher zusaetzlich 8 stabile Baryonen mit
Charm, darunter zwei mit C=+2.
Genau so kann das b-Quark an Stelle des d- oder s-Quarks treten.
Kernbetazerfaelle:
a) wovon haengt die Lebensdauer eines Betazerfalls ab? Welcher Faktor ist ‚trivial‘ und wovon haengt
er ab (Naeherungsformel?).
B) was lernt man aus den ft-Werten? Warum sind sie so verschieden?
C) wann ist ein Betazerfall erlaubt, wann ‚verboten‘? Wie aeussert sich das in Lebensdauer und Spektrum?
Beispiele?
D) Skizzieren Sie den Verlauf der Bindungsenergie fuer A= 160 als Funktion von Z. Welche
Betazerfaelle sind moeglich?
Antworten:
a) G=1/t= |Mif|2 * Phasenraum *F(Z,E) (Fermis goldene Regel)
Der Phasenraumfaktor ist trivial, ebenso die fermifunktion, die eine Korrekturfunktion fuer el.magn.
WW ist. Phasenraum ~ Q5, wenn Q der Q-wert des Zerfalls ist .
B) der ft-Wert ist ~ |Mif|2 , also korrigiert auf triviale kinematische Faktoren. Kleine ft-Werte gehoeren zu
erlaubten Zerfaellen, hohe zu verbotenen.
C) erlaubt sind Betazerfaelle, bei denen sich der Spin der Kerne um Null oder 1 aendert. Bei verbotenen
Zerfaellen muss das Leptonpaar einen Bahndrehimpuls relativ zum Kern aufnehmen (Beispiel 40K).
Diese haben lange Lebensdauer und meist energieabhaengige Matrixelemente (Kurieplot nicht gerade)
D) es gibt naeherungsweise 2 Parabeln fuer uu und gg Kerne, die sich um die Paarungsenergie
unterscheiden. Dann kann es bis zu 2 stabile Isobare geben. Ein Nuklid kann sowohl b+ als auch bZerfaelle haben.
Paritaetsverletzung:
a) Wie sieht die Paritaetsoperation P aus? Wie aendert sich eine Wellenfunktion unter P?
Wann ist die Paritaet verletzt?
B) Welche Messgroessen erlauben es, Paritaetsverletzunng zu beweisen. Diskutieren Sie das am
Beispiel des Neutronzerfalls.
Antworten:
a) Die Paritaetsoperation ist die Spiegelung am Ursprung. P Y(r)=Y(-r)
Die Paritaet ist verletzt, wenn in der Natur ein beobachteter Zustand und der am Ursprung
gespiegelte nicht mit gleicher Hauefigkeit auftreten.
B) gesucht sind ‚pseudoskalare‘ Messgroessen, die unter P das Vorzeichen aendern. Diese lassen
sich als Skalarprodukt aus Vektor und Axialvektor konstruieren.
a
pe
Polarisiertes Neutron: Beobachtet werden koennen:
- der Impuls pe des Zerfallselektrons
- die Helizitaet H des Zerfallselektrons
- der Rueckstoss des Protons (und damit die Neutrinorichtung)
p e . sn , p e . se , ( p e
sn
pn) . sn
Alle Terme proportional diesen Groessen muessen
verschwinden, wenn die Paritaet erhalten ist.
Kernschalenmodell:
a) wie machen sich magische Zahlen bemerkbar?
B) wie sieht das Potential im Kernschalenmodell aus? Warum macht es Sinn, von einem mittleren
Potential eines Nukleons zu reden?
C) wo in der (Z,N) Ebene liefert das Kernschalenmodell gute Resultate?
D) diskutieren Sie im Kernschalenmodell:
- die Isomerie von Kernen (Inseln der isomerie)
- magnetische Momente
-Quadrupolmomente
Antworten:
a) hohe Bindungsenergie des letzten Nukleons, grosser Energieabstand des 1. Angeregten Niveaus
b) V = V( ri ) + Vls( ri ) li . si , dabei ist V( ri ) ein Zentralpotential des Nukleons i im mittleren
Potential der anderen. Dies ist moeglich weil ein Nukleon im Kern eine relativ grosse freie
Weglaenge hat, da es nur mit Nukleonen an der Fermikante stossen kann.
C) gute Resultate liefert es nur in der Naehe abgeschlossener Schalen, die Spin Null haben und
kugelsymmetrisch sind. Am besten nur ein Nukleon ausserhalb.
D) die SpinbahnWW fuehrt zu einer sehr starken Absenkung von Zustaenden mit hohem
Bahndrehimpuls. Daher liegen Niveaus mit stark unterschiedlichem Spin nahe zusammen.
- Isomerie: Grundzustand und 1. Angeregter Zustand haben sehr unterschiedlichen Spin --> hoher
Multipoluebergang erforderlich.
- Magn. Momente: simple Voraussagen fuer kerne mit einzelnen Nukleonen ausserhalb geschlossener
Schalen. Der kernspin ist gleich dem Spin des einzelnen Nukleons ( Summe aus Bahn- und Eigenmoment)
- Quadrupolmomente messen die Deformation der Kerne von der Kugelgestalt: sehr klein nahe
magischer Zahlen, gross dazwischen.
Kernspaltung:
a) wie sieht die Neutronbilanz in einem Reaktor aus ( dessen Kern sei sehr gross)
, wie wird die Kettenreaktion gesteuert?
B) wie sieht die Energiebilanz aus?
C) welche Spaltprodukte entstehen? Diskutieren Sie die Nachwaerme und das radioaktive Inventar
(qualitativ) eines Reaktors nach laengerer Betriebszeit.
Antworten:
A) die Zahl der fuer eine neue Spaltung verfuegbaren Neutronen nach einem Spaltzyklus ist (dabei
sind Leckverluste vernachlaessigt):
k= h e p f , h= Neutronen/Spaltung von 235U; e=Schnellspaltfaktor (238U); (1-p) = Verlust bei
Moderation (Resonanzeinfang), (1-f) = Verlust thermischer Neutronen im Moderator
b) insgesamt werden etwa 200 MeV/Spaltung frei, ueberwiegend als Rueckstossenergie der Spaltprodukte,
die sich als thermische Energie bemerkbar machen, 20 MeV davon entsthen verzoegert (Nachwaerme)
durch radioaktive Zerfaelle und Gammastrahlung.
C) die Spaltkerne sind asymmetrisch verteilt mit Maxima bei ca. A=90 und 140 (das ist ein Effekt der
magischen Zahlen). Zusaetzlich entstehen ca. 2.3 Neutronen. Die Spaltprodukte sind neutronreich
und zeigen daher b- -Zerfaelle. Nach dem Abschalten macht die Nachwaerme bis zu 10% der Energieerzeugung im Betrieb aus. Neben den Betastrahlern sind auch Transurane vorhanden insbesondere
Plutoniumisotope mit Lebensdauern von ~50000 y. Wichtige langlebige Isotpe sind: 135J, Sr, 135Cs
Stabilitaet von Sternen:
Wodurch stabilisieren sich Sterne gegen den Gravitationsdruck?
A) Sterne, die Energie durch Fusion gewinnen
b) weisse Zwerge und Neutronsterne.
Welche Gebilde sind stabil und bis zu welcher Massengrenze? Wie sehen jeweils die
Zustandsgleichungen aus?
Antworten:
A) der Gravitationsdruck wird durch den thermischen Druck kompensiert: p/r ~ T
b) der Gravitationsdruck wird jeweils durch den fermidruck der Elektronen bzw. Neutronen
kompensiert: p/r ~ (r/rc)n/3 , dabei ist rc ein kritische Dichte und n=2 fuer nichtrelativistische
Teilchen --> n=1 fuer relativistische.
Weisse Zwerge sind stabil bis ca. 1.5 Sonnenmassen, Neutronensterne bis ca. 3.2 Sonnenmassen.
Darueber entsteht ein schwarzes Loch.