Funktionen Einführung

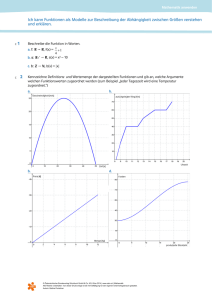
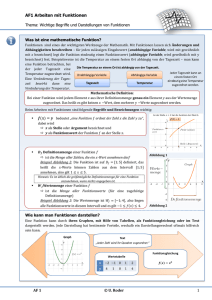
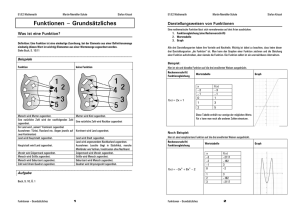
Funktionen
RF + KP 6/2012
Funktionen
f ( x)  2x
f ( x)  3x3 10x2  2
2
f (x)  sin x
f ( x)  3x
f ( x)  2 x
1 x
f (x) 4x  2
Beispiele für Funktionen ?
 Notenspiegel
 Temperatur einer Flüssigkeit beim Abkühlen
zum Zeitpunkt x
 Ein Essen kostet in der Mensa 3,45 Euro.
Es wird von verschiedenen Personen
genommen und in Münzgeld bezahlt.
 Verlauf des DAX an einem Börsentag
 Benötigte Menge Farbe zum Streichen
verschiedener Flächen
Zuordnungen
 Elemente einer Definitionsmenge
werden auf Elemente einer
Wertemenge abgebildet.
 Z.B.: Anna, Bertha, Christof und
Darius besitzen Haustiere
A
B
C
D
D
Hund
Zwergwachtel
Tarantel
W
Definition „Funktion“
 Eine Funktion f(x) ist eine Zuordnung,
die jedem Element x der
Definitionsmenge D genau ein
Element der Wertemenge W
zuordnet.
A
B
C
D
D
Hund
Zwergwachtel
Tarantel
W
Definition „Funktion“
 Eine Funktion f(x) ist eine Zuordnung,
die jedem Element x der
Definitionsmenge D genau ein
Element der Wertemenge W
zuordnet.
D
A
B
C
D
E
Ist das auch
eine Funktion?
Hund
NEIN, da dem Element E aus der
Definitionsmenge kein Wert in der
Wertemenge zugeordnet ist!
Zwergwachtel
Tarantel
W
Beispiele für Funktionen
Diese Darstellung ist der
klassische Notenspiegel.
1. Beispiel: 1 2 3 4 5 6 Ist das eine
 Notenspiegel
2 4 5 0 1 1
2. Beispiel: eine
eine
eine
eine
1
2
3
4
Funktion?
Ja
haben:(Anna, Can)
haben: (Dora, Ali, Hans, …)
haben: (Karl, Frida, Secil, …)
haben: …
Ist das eine
Funktion?
NEIN
Bitte überlegen Sie nochmals!
Beispiele für Funktionen?
 Notenspiegel Kommt etwas darauf an
ja  Temperatur einer Flüssigkeit beim Abkühlen
zum Zeitpunkt x
 Ein Essen kostet in der Mensa 3,45 Euro.
Kommt etwas darauf an
Es wird von verschiedenen Personen
genommen und in Münzgeld bezahlt.
ja  Verlauf des DAX an einem Börsentag
ja  Benötigte Menge Farbe zum Streichen
verschiedener Flächen von gleicher
Beschaffenheit
Funktionsklassen:






Lineare Funktionen
Quadratische Funktionen
Ganzrationale Funktionen
Gebrochenrationale Funktionen
Trigonometrische Funktionen
Exponential- und
Logarithmusfunktionen
Mehr dazu in der folgenden Gruppenarbeit!
RF + KP 5/2012