Zuordnungen - s-hb.de VIRTUAL CLASSROOM

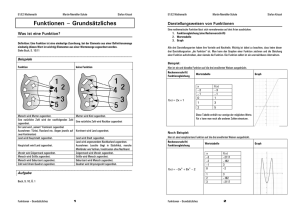
Zuordnungen
Z
A
1
1
D
Zuordnungen unterscheiden sich:
2
2
W
3
3
Durch die Zuordnungsvorschrift x < y wird den
Zahlen einer Ausgangsmenge A ={1; 2; 3}
Zahlen einer Zielmenge Z = {1; 2; 3} zugeordnet.
Die Zuordnung ist nicht für alle Zahlen erklärt. D.h.: Nicht jeder Zahl aus A wird eine Zahl
zugeordnet.
Die Definitionsmenge D umfasst nur die Zahlen 1 und 2:
In gleicher Weise werden nicht alle Zahlen der Zielmenge Z erfasst.
Die Wertemenge W umfasst nur die Zahlen 2 und 3.
Besondere Zuordnungen: Funktionen
D = {1; 2}
W = {2; 3}
Z
A
1
Eine Zuordnung heißt Funktion, wenn jeder
Zahl der Definitionsmenge genau ein Element
der Wertemenge zugeordnet wird. Die oben
aufgeführte Zuordnung x < y ist folglich keine
Funktion!
Aber die Zuordnung x → x + 1 in der Abbildung
rechts ist dagegen eine Funktion!
D
1
2
3
2
W
3
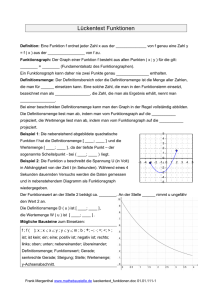
Schreibweisen werden vereinbart...
Funktionen bezeichnet man im Allgemeinen mit kleinen Buchstaben: f, g, h ... wie im
folgendem Beispiel:
f: x → x + 1 .
Der Term "x + 1" heißt Funktionsterm. Mit Hilfe des Funktionsterms lässt sich durch
Einsetzen einer Zahl aus der Definionsmenge an die Stelle des Platzhalters x der
zugeordnete Wert aus der Wertemenge berechnen:
x = 2:
f: x → x + 1
f: 2 → 2 + 1 bzw. f: 2 → 3
Der der Zahl 2 zugeordnete Wert 3 heißt Funktionswert an der Stelle 2 und wird mit f(2)
(lies: "f von 2") abgekürzt: f(2) = 3. Allgemein bezeichnet man daher die Funktionswerte an
der Stelle x mit f(x) (lies: "f von x").
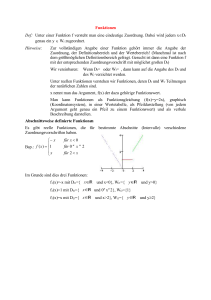
Eine Funktion ordnet jedem x der Definitionsmenge einen Funktionswert f(x) aus der
Wertemenge zu:
f: x → f(x)
Im oberen Beispiel: f: x → x + 1 gilt folglich für den Funktionswert
stets:
f(x) = x + 1 (Funktionsgleichung).
Oftmals wird statt f(x) auch einfach der Buchstabe y benutzt. Auf diese Weise erhält man
folgende gleichwertige Schreibweisen:
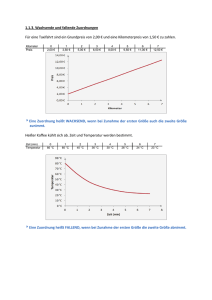
Zuordnungsvorschrift:
f: x → f(x)
Funktionsgleichung:
f(x) = x + 1
oder
y =x+1