Funktionen - Lyrelda.de

Funktionen
Funktionen
Zeichenerklärung:
Ly-1234
für passendes Video anklicken
oder nach dem Code auf www.lyrelda.de suchen
Wichtig!
Achtung! Häufige Fehlerquelle
www.lyrelda.de
1
Funktionen
1 Funktionen
Ab der Mittelstufe bilden die Funktionen eines der zentralen Themen der Schulmathematik. Wir wollen zuerst den Begriff der Funktion allgemein klären.
Funktion
Mat-70797
eine Funktion ist eine eindeutige Zuordnung, so dass jeder Zahl x aus einer Definitionsmenge genau eine Zahl y aus der Wertemenge zugeordnet ist. Eine Funktion ist
also eine Zuordnung
Eine Funktion lässt sich auf verschiedene Weisen Darstellen
Beispiel 1
Gewöhnlich gibt man der Funktion einen Namen, meistens f,g oder
h. Eine Zuordnung erfolgt dann per Funktionsgleichung:
f (x) = 2 · x
x ∈ R,
jedem Wert x, aus der Definitionsmenge R, wir somit der dazu doppelte Wert y
zugeordnet, deshalb schreibt man manchmal auch etwas kürzer:
y = 2 · x.
Beispiel 2
Man kann eine Funktion auch als (Werte-)Tabelle darstellen
x
-2 -1
f(x) -4 -2
0 1 2
0 2 4
oder eben auch
x
y
-2 -1 0
-4 -2 0
1 2
2 4
Beispiel 3
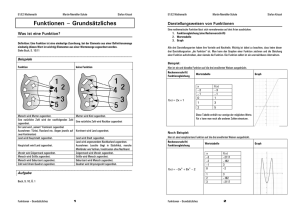
am anschaulichsten ist jedoch ein (Funktions-)Graph als Schaubild
der Funktion! Die waagrechte Achse („Abzisse“) zeigt dabei den x-Wert an , die
senkrechte Achse („Ordinate“) gibt die Funktionswerte an. Man sagt oft einfach
auch x- bzw. y-Achse. (siehe Abbildung 1)
Definitionsbereich
Der Definitionsbereich einer Funktion f heißt Df . Er enthält die Zahlen, die man für
x in die Funktionsgleichung einsetzen darf.
Wertebereich
Der Wertebereich einer Funktion f heißt Wf . Er umfasst alle Funktionswerte, die
diese Funktion annehmen kann
www.lyrelda.de
2
Funktionen
Abbildung 1: Funktionsgraph der Funktion f(x)
Beispiel 4
In unsere Funktion f (x) = 2x dürfen wir jede Zahl einsetzen, die wir
wollen, die maximale Definitionsmenge ist also Df = R, ebenso kann die Funktions
jeden beliebigen Wert annehmen und somit gilt auch Wf = R.
Schauen wir uns aber einmal die Funktion g(x) = x12 an, so bemerken wir, dass wir
die Null nicht einsetzen dürfen und nur positive Werte von der Funktion angenommen werden, es folgt also: Dg = R∗ und Wg = R∗+
Noch kurz ein paar Hinweise zur Notation von Intervallen:
Df = {x| − 1 ≤ x ≤ 2} = [−1; 2]
Diese beiden Schreibweisen bedeuten das Gleiche, man darf alle Zahlen zwischen
Minus-Eins und Zwei einsetzen, einschließlich der Minus-Eins und Zwei. Will man
eine davon (oder beide) ausschließen, so muss das entsprechende ≤ durch eine <
ersetzen, bzw. eine runde Klammer statt der eckigen Klammer benutzen. Nehmen
wir zum Beispiel an, dass die Zwei nun ausgeschlossen werden soll, so sieht das ganze
so aus:
Df = {x| − 1 ≤ x < 2} = [−1; 2)
Will man nun weiter nur ganze Zahlen benutzen, so kann man das wie folgt notieren:
Df = {x| − 1 ≤ x < 2 , x ∈ Z} = {x| − 1 ≤ x < 2}Z = [−1; 2)Z
Das würde bedeuten es sind nur -1, 0 und 1 als x-Werte erlaubt.
www.lyrelda.de
3