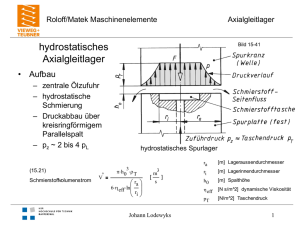
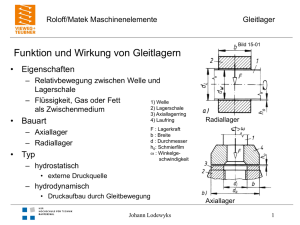
Schraubenfedern
Werbung

Roloff/Matek Maschinenelemente Schraubenfedern Schraubenfedern – Merkmale • • • • • häufigste Federform in der Regel rechts steigend entspricht einer schraubenlinienförmigen Drehstabfeder Druck- oder Zugfeder kalt- oder warmgeformt Material – legierter Federstahl » Sorte von A bis D für steigende Kräfte – unlegierter Federstahl » Sorte FD für statische, VD für dynamische Last • Oberflächenschutz – geölt oder gefettet – Kunststoff beschichtet Johann Lodewyks 1 Roloff/Matek Maschinenelemente Drahtdurchmesser Schraubenfedern kaltgeformt warmgeformt d 17mm d De Di Windungsdurchmesser D 2 200mm 8...60mm De 460mm Federlänge L0 630mm L0 800mm Anzahl der wirksam federnden Windungen n2 n3 Wickelverhältnis w D d (10.36) Anzahl der Windungen 4...20 n2 nt [-] Bild 10-23 D w 3...12 d [n-t ] n 1.5 [-] (10.37) Summe der Mindestabstände bei statischer Last 2 D Sa 0.0015 0.1 d n [ m ] Sa 0.02 ( D d ) n [ m ] d (10.37) Summe der Mindestabstände bei dynamischer Last Sa ¦ 1.5 Sa [ m ] Sa ¦ 2 Sa Johann Lodewyks [m] 2 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-23 Federenden • b) angelegte, unbearbeitete Federenden • c) angelegte, geschmiedete Federenden (10.38) Blocklänge (10.38) Blocklänge angelegt und geschliffen Lc n t d max angelegt und planbearbeitet angelegt und unbearbeitet Lc n t 1.5 d max [m] Lc n t 1.1 d max [m] statische Last kleinste zulässige Federlänge bei maximaler Last Ln (10.40) statische Last L0 [m] unbearbeitet (10.39) Länge der unbelasteten Feder Lc n t 0.3 d max [m] Lc Sa s c Lc dynamische Last [m] Ln ¦ Lc Sa ¦ [ m] dynamische Last s n Lc Sa [ m ] Johann Lodewyks ¦ L0 s c Lc s n Lc Sa ¦ [m] 3 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-24 Zugfedern • Eigenschaften – keine Führungselemente notwendig – meist rechtsgewickelt – Für d>17mm warmgeformt ohne Vorspannung – Bis d=17mm kaltgeformt mit anliegenden Windungen und Vorspannung (10.41) Beispiel einer Zugfeder mit 90° versetzten deutschen Ösen LH~Di und Ösenöffnung m>2d ohne Berücksichtigung der Ösen Länge der unbelasteten Feder LK nt 1 dmax [ m] Johann Lodewyks mit Berücksichtigung der Ösen L0 LK 2 LH [ m] 4 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-25 Zugfederösen • Typen – a) halbe deutsche Öse – b) doppelte deutsche Öse – c) ganze deutsche Öse, seitlich hochgestellt – d) Hakenöse – e) englische Öse – f) Haken eingerollt (eingerollte Windungen nicht federnd) – g) Gewindestopfen Johann Lodewyks 5 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-26 Berechnung von Druck- und Zugfedern mit Kreisquerschnitt – Abschätzung des Drahtdurchmessers mit Größengleichung • Entsprechend konstruktiver Vorgaben wird mit De oder Di gerechnet (10.42) Abschätzung, Grössengleichung [N] [mm] Federdurchmesser Drahtdurchmesser De Di [mm] innerer Windungsdurchmesser d < 5mm d M [Nmm] Moment A , B, C, D k1 0.15 k1 0.16 FD , VD k1 0.17 k1 0.18 k1 d k1 F De [-] Drahtsorte Kennwert 3 F Drahtdurchmesser Kennwert 3 Einheiten der Grössengleichung k2 k1 F Di k2 [ mm ] 3 2 k1 Fmax Di 3 Di 5...14mm 2 [-] Johann Lodewyks maximale Federkraft • Auswahl: – Durchmesser d nach (DIN 2076, TB 10-2a) – Windungsdurchmesser D nach (DIN 323, TB 1-16) 6 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-26 Berechnung von Druck- und Zugfedern mit Kreisquerschnitt • Festigkeitsnachweis mit Durchmesser • Berechnung entspricht Drehstab • Kraft F mit Hebelarm D/2 verändert den Windungsabstand proportional • Modell einer Windung als Drehstab • Belastung entspricht einem Torsionsmoment T – Grundgleichungen: Momentenbelastung polares Widerstandsmoment eines Kreisquerschnitts T Wp F D [ Nm ] 2 p d 3 3 [m ] 16 ¦ Federweg s n s Länge des gestreckten Federdrahtes l p D n Volumen des Federdrahtes V p 4 2 [ m] F [N] maximale Federkraft ¦ [ m] l [m] Drahtlänge D [m] mittlerer Windungsdurchmesser d [m] Drahtdurchmesser 3 d l [ m ] Johann Lodewyks 7 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-26 Berechnung von Druckfedern mit Kreisquerschnitt – Festigkeitsnachweis für statische Last (10.43) Schubspannung Zustand 1 t1 D F1 2 p 16 (10.43) Schubspannung Zustand 2 t2 d Schubspannung im Blockzustand tc p d D Fc 2 p 16 F1 , F2 Fc 3 d 3 N ] 2 m D F2 2 16 (10.43) tzul [ 3 tzul [ Federkraft im Zustand 1, 2 [N] Federkraft im Blockzustand ] 2 m tczul [N] N [ N ] 2 m Fc tzul tczul [N/m^2] Maximal zulässige Schubspannung nach (TB 10-11) Johann Lodewyks [N/m^2] Maximal zulässige Schubspannung im Blockzustand nach (TB 10-11) 8 Roloff/Matek Maschinenelemente Berechnung von Druckfedern mit Kreisquerschnitt Schraubenfedern Bild 10-27 – Festigkeitsnachweis für dynamische Last (10.44) tk1 korrigierte Schubspannung im Zustand 1 k t1 tkO [ N ] 2 m (10.44) tk2 korrigierte Schubspannung im Zustand 1 k t2 tkO [ N ] 2 m (10.44) korrigierte Hubspannung tkh tk2 tk1 tkO tkU N ] 2 m tkO Beiwert der Drahtkrümmung nach (TB 10-11d) [N/m^2] korrigierte Oberspannung Zeit- oder Dauerfestigkeitswert tkU [N/m^2] k [ [-] korrigierte Unterspannung Zeit- oder Dauerfestigkeitswert Johann Lodewyks 9 Roloff/Matek Maschinenelemente Schraubenfedern Berechnung von Druckfedern mit Kreisquerschnitt • Berechnung der Windungsanzahl: (10.45) Anzahl wirksamer Windungen n ¦ 4 G d s 8 3 D F G 8 d 4 [-] 3 D Rsoll • Auswahl der Windungsanzahl n ~ n´ • Berechnung der Kennwerte: (10.46) gewählte Federrate Rist (10.47) Federkraft [ F Rist s Rsoll [N/m] Sollfederrate 4 F Rist s N G d s 8 3 D n m ] Federweg s 3 F Rist s (10.48) 4 G d s 8 3 D n [N/m^2] Gleitmodul (10.48) 4 G d 8 3 D n G [ N] Federungsarbeit Johann Lodewyks WF 8 D n F G 4 d F s 2 s [m] 1 V t 4 G 2 [ Nm ] 10 Roloff/Matek Maschinenelemente Berechnung von Zugfedern mit Kreisquerschnitt Schraubenfedern Bild 10-28 • Besonderheiten der Zugfederberechnung – Federn nur statisch belasten, wegen Ösen und Kugelstahlen bei anliegenden Windungen nicht möglich – genormt nach DIN 2089 T2 – reduzierte Spannung zulässige Spannung t bei Zugfedern (TB 10-19) zul Rm [N/m^2] 0.45 Rm [ N ] 2 m Zugfestigkeit Johann Lodewyks 11 Roloff/Matek Maschinenelemente Schraubenfedern Berechnung von Zugfedern mit Kreisquerschnitt (10.51) Federrate R F F F0 s s (10.54) 4 G d 8 3 D n [ (10.52) innere Vorspannkraft m Anzahl wirksamer Windungen ] F0 F R s F0 t0zul 0.4 d G d s F 8 3 D n [N] Gesamtzahl der Windungen nt G 8 4 d s 3 [-] D F F0 LK d 1 [-] 3 [N] (10.56) D Federungsarbeit Schubspannung entsprechend dem Herstellverfahren nach (TB 10-19b) n (10.55) 4 (10.53) erreichbare innere Vorspannkraft N t0zul tzul F0 G [N] F F0 s [ Nm ] 2 innere Vorspannkraft [N/m^2] Gleitmodul LK [m] tzul [N/m^2] Johann Lodewyks WF Länge der unbelasteten Feder Schubspannung nach (TB 10-19a) 12 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-29 Zylindrische Schraubenfeder mit Rechteckquerschnitt • Unterschied zum Kreisquerschnitt – – – – teuer bessere Raumausnutzung schlechtere Materialausnutzung ungleichmässige Spannungsverteilung durch starke Verformung – Berechnung nach DIN 2090 flachgewickelt - härter Johann Lodewyks hochkantgewickelt 13 Roloff/Matek Maschinenelemente Schraubenfedern Bild 10-30 Kegelige Schraubendruckfedern • Eigenschaften a) u. b) – meist Kreis- selten Rechteckquerschnitt – größte Schubspannung bei D2 • Eigenschaften c) – schlechte Werkstoffausnutzung – gute Raumausnutzung – Einsatz • Puffer • Zangen, Scheren Kreisquerschnitt Johann Lodewyks Rechteckquerschnitt Pufferfeder mit abnehmendem Rechteckquerschnitt 14