Vortragsfolien - Didaktik der Physik

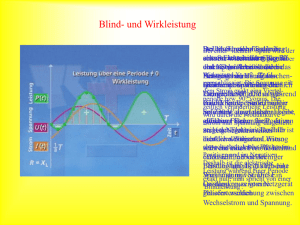
Physics Teachers Day
Osnabrück 25. September 2008
Energieübertragung durch
elektrischen Strom und
elektromagnetische Felder
U. Backhaus, Universität Duisburg-Essen
Gliederung
•
•
•
•
•
Problemstellung
Lösungsidee
Fachliche Grundlagen: Lokale Energieerhaltung
Poynting-Maxwell‘sche Lösung und Alternativen
Beispiele
–
–
–
–
Gleichströme
Transformatoren
Wellenleiter
Hertz‘scher Dipol
• Didaktische Diskussion
Problemstellung
• Der Energiebegriff spielt im Physikunterricht der
allgemeinbildenden Schulen in den letzten Jahren eine
ständig wachsende Rolle.
• Wurde die Energie früher als eine Art
Bilanzierungsgröße eingeführt, die den Ablauf von
Prozessen steuert, so beruht heute ihre Anschaulichkeit
auf der Betonung ihres extensiven Charakters und ihrer
Mengenartigkeit. Diese Eigenschaft hat zur Folge, dass
man sich vorstellen kann, Energie sei in einem Körper
enthalten und sie werde zwischen Körpern
ausgetauscht.
• Die Unanschaulichkeit von Fernwirkungen führt dazu,
Energieerhaltung nicht nur global, sondern auch lokal
anzunehmen und den Energieaustausch zwischen zwei
Systemen deshalb durch einen Energiefluss zu
beschreiben.
Energieübertragung durch elektrischen Strom
• Es ist offensichtlich: Am Generator wird Energie in den
Stromkreis eingespeist, und an dem Lämpchen wird
(ebenso viel) Energie abgegeben.
• Aber: Wie (genau) gelangt die Energie vom Generator
zur Lampe: durch die Kabel (durch welches?), durch den
Zwischenraum oder auf ganz anderen Wegen?
Zitate zur Einstimmung
•
•
•
•
•
„Das kindliche Modell von den energiebeladenen Elektronen, welche die
elektrische Energie gleichsam vom Erzeuger zum Verbraucher tragen, geht
weit an der Wirklichkeit vorbei.“ (Rang)
„Dass die Energie nicht mit den Elektronen zur Energiequelle zurückfließt,
war nach der Diskussion allen Schülern klar und nachfolgend der
Widerspruch, dass sich Elektronen voneinander unterscheiden sollen, je
nachdem ob sie vor oder hinter der Lampe fließen sollen.“ (Rückl)
„Diese mysteriöse zirkulierende Energieströmung, die zunächst so
lächerlich erschien, ist absolut notwendig.“ (Feynman)
„Ehe wir uns mit einigen Anwendungen der Poynting‘schen Formeln …
beschäftigen, möchten wir sagen, dass wir sie nicht wirklich ,bewiesen'
haben. Wir haben lediglich ein mögliches u und ein mögliches S gefunden.
… De facto gibt es unendlich viele verschiedene Möglichkeiten für u
und S, und bisher hat noch niemand über eine experimentelle Möglichkeit
nachgedacht, mit der man sagen könnte, welche die richtige ist.“ (Feynman)
„Die Frage, inwieweit andere Lösungen … ebenfalls sinnvoll sind, ist bisher
kaum diskutiert worden. Man begnügt sich allenthalben mit der durch
(den Poynting‘schen Ausdruck) gegebenen einfachsten Lösung, denn S
ist sowieso nicht direkt messbar.“ (Rang)
Lösungsidee
• Die gesamte Energie, die von der Batterie zum
Verbraucher gelangt, muss durch eine (unendliche)
Fläche fließen, die die beiden trennt. Sie kann
berechnet werden, indem die Energieflussdichte S
über die gesamte Fläche integriert wird.
• Es konkurrieren zwei alternative Ausdrücke:
SP = E x H und Sn=Φj
• Beide Ausdrücke führen zu demselben Ergebnis,
aber: SP ist nur außerhalb der Kabel von null
verschieden, Sn nur innerhalb.
Lösungsidee
• Die gesamte Energie, die von der Batterie zum
Verbraucher gelangt, muss durch eine (unendliche)
Fläche fließen, die die beiden trennt. Sie kann
berechnet werden, indem die Energieflussdichte S
über die gesamte Fläche integriert wird.
• Es konkurrieren zwei alternative Ausdrücke:
SP = E x H und Sn=Φj
• Beide Ausdrücke führen zu demselben Ergebnis,
aber: SP ist nur außerhalb der Kabel von null
verschieden, Sn nur innerhalb.
Der Poynting‘sche Satz 1
Begriffsbildung
Der Poynting‘sche Satz 2
.
.
Eigenschaften des
Energieflusses
nach Maxwell und Poynting
Geladener Körper im homogenen
Magnetfeld
Zweidraht-Leitung
Zweidraht-Leitung
(Galili et al., Am. J. Phys. 2005)
Zweidraht-Leitung
(Majcen et al., Am. J. Phys. 2000)
Zwei galvanisch getrennte
Stromkreise
Zwei galvanisch getrennte
Stromkreise
Wahlmöglichkeiten
„neue“ Alternative zum Poynting-Bild
elektrodyn. Potentiale
Beispiel Gleichstrom
Wahlmöglichkeiten
Gleichstrom: Energiestrom in einen Widerstand
Poynting
„neu“
Gleichstrom: Energiestrom beim
Aufladen eines Kondensators
Poynting
„neu“
„potentielle Energie elektrisch geladener Körper“
Gleichstrom: Energiestrom in eine Spule bei
zunehmender Stromstärke
„potentielle Energie stromführender Kabel“
Beispiel Wechselstrom
Solange einzelne Stromkreise betrachtet werden, haben elektrisches Feld und
Potential und magnetisches Feld und Potential jeweils dieselbe Zeitabhängigkeit.
Für Wechselstrom ergeben sich bei einzelnen Stromkreisen
dieselben Energieflussbilder!
Wechselstrom: Der Transformator
(Vereinfachungen: Zylindersymmetrie und
konstante Stromsteigerung in der Primärspule)
Poynting:
Der Energiefluss von der Quelle zum Verbraucher umgeht den Transformator.
Wechselstrom: Der Transformator
(Vereinfachungen: Zylindersymmetrie und
konstante Stromsteigerung in der Primärspule)
„neu“:
Der Energiefluss von der Quelle zum Verbraucher
strömt von der Primärspule zur Sekundärspule.
Wechselstrom: Der Transformator
(Vereinfachung: langer Trafo)
Hochfrequente Ströme und Felder:
Der Wellenleiter
Poynting:
Der Energietransport geschieht ausschließlich im Zwischenraum.
Eine kleine Energieströmung in den Kabeln versorgt die sich ändernde Feldenergie.
Hochfrequente Ströme und Felder:
Der Wellenleiter
„neu“:
Der Energietransport geschieht ausschließlich in den Kabeln.
Hochfrequente Ströme und Felder:
Der Hertz‘sche Dipol
Das elektrische Feld
Hochfrequente Ströme und Felder:
Der Hertz‘sche Dipol
Die Energieabstrahlung nach Poynting
Hochfrequente Ströme und Felder:
Der Hertz‘sche Dipol
Die Energieströmung im „neuen“ Bild
Didaktische Konsequenzen
• Alle Darstellungen sind mit der Kontinuitätsgleichung für die Energie
verträglich. Sie können deshalb sicher nicht in Widerspruch zu der
Forderung nach Energieerhaltung geraten. Will man eindeutige Aussagen
über Dichte und Stromdichte der Energie erreichen, müssen also
zusätzliche Argumente herangezogen werden:
• „Man hat vermutet, dass die einfachste Möglichkeit die richtige ist, aber wir
müssen zugeben, dass wir nicht sicher wissen, welche die wirkliche
Lokalisierung der elektromagnetischen Feldenergie im Raum beschreibt.“
(Feynman)
• Es scheint bis heute keine allgemein akzeptierten Argumente zu geben, mit
deren Hilfe sich eindeutige Ausdrücke für Dichte und Stromdichte der
Energie in elektromagnetischen Feldern ergeben. Aber selbst wenn es
solche Argumente gäbe, dann müssten diese den Lernenden genannt
werden können. Mindestens müsste darauf hingewiesen werden, dass die
Darstellung eines bestimmten Energieflussbildes weit über die den
Lernenden bekannten Phänomene hinausgeht und dass es andere mit
diesen verträgliche Darstellungen gibt.
Jede Theorie sollte so lange und so fest wie
möglich in der Alltags- und Erfahrungswelt
der Lernenden verankert werden. Dabei
sollte dem Lernenden jedoch der
Unterschied zwischen dem Phänomen auf
der einen Seite und der Verwendung des
Phänomens in der Theorie auf der anderen
Seite klar werden. Er kann ganz gut
verstehen, dass es keinen zwingenden Weg
von den Phänomenen zur Theorie gibt.
Theorie ist immer eine produktive Antwort
auf die Phänomene! (W. Jung 1979)
„Was ein Mensch sieht, hängt sowohl
davon ab, worauf er blickt, wie davon,
worauf zu sehen ihn seine visuellbegriffliche Erfahrung gelehrt hat.“
(T. S. Kuhn)
Literatur
• Backhaus, U.: PdN/Physik 36/3, 30 (1987)
(http://www.didaktik.physik.uni-due.de/~backhaus/publicat/Energietransport.pdf)
• Backhaus, U.: Westarp: Essen, Magdeburg
1993
(http://www.didaktik.physik.uni-due.de/~backhaus/publicat/Energie.pdf)
• Majcen, S. et al: Am. J. Phys. 68/9, 857 (2000)
• Galili, I. et al.: Am. J. Phys. 73/2, 141 (2005)
Begriffsbildung:
Erhaltungsgrößen
Begriffsbildung:
Übertragung mengenartiger Größen
Begriffsbildung:
Strömung und Dichte
mengenartiger Größen
Wahlmöglichkeiten
bei der Energieströmung
durch Umeichung des Potentials Φ
+
-
Energietransport
durch eine unendliche Ebene
-
Die Maxwell-Gleichungen
Die elektrodynamischen Potentiale
Eichtransformationen
Coulomb-Eichung bei Wechselstrom
Zur Ableitung des
Poynting‘schen Satzes