teilchenphysikI

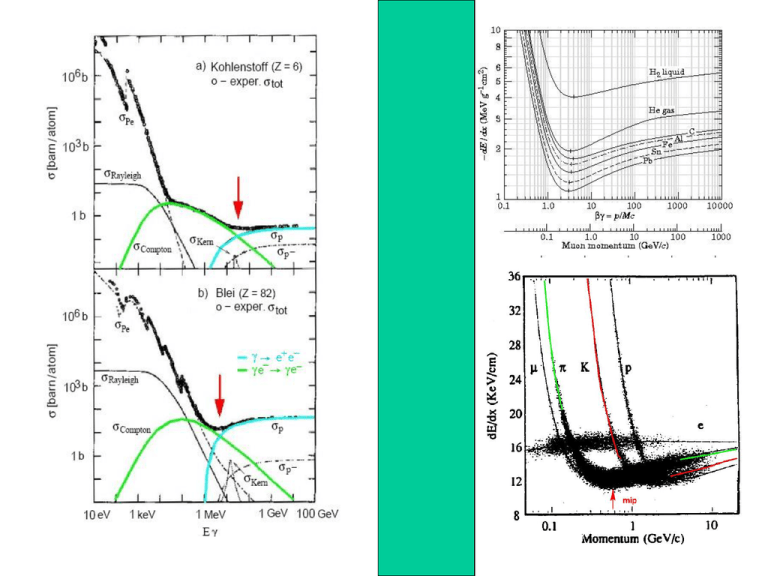
Teilchenphysik: Verständnisfragen
Frage: welche Detektoren sind im Bereich von keV bis GeV zur
Energiemessung von Gammas geeignet?
1. Detektoren für Messung von Gammaenergien:
Im Energiebereich bis ca. 300 keV ist die Effizienz für Photoeffekt bei hohem Z
noch relativ hoch, das freigesetzte Elektron hat dann die Énergie des Gammas minus Bindungsenergie des Elektrons. Dann sind total absorbierende Zähler wie Germanium HL Zähler
sehr gut geeignet. Bei kleineren Energien is 15 keV werden auch die viel billigeren
Proportionalzähler benutzt. Deren Auflösung ist allerdings deutlich schlechter (wieso??).
Bei Energien oberhalb 500 MeV und unterhalb ca. 5 MeV dominiert die Comptonstreuung.
Diese gibt ein kontinuierliches Spektrum im Detektor. Dieser Bereich ist schwierig, es
werden oft grossvolumige Szintillationszähler genutzt (NaJ)
Bei wesentlich höheren Energien dominiert dann die Paarbildung und später die el.magn
Schauerbildung- Schauerzähler (Kalorimeter).
Frage: wie lassen sich Elektronen, Myonen und Hadronen experimentell identifizieren?
2.
Trennung von Elektronen, Müonen, Hadronen Bereich.
Elektronen: Schauerbildung, TRD und bei kleinen Energien Cerenkovzähler
Vergleich von Impulsmessung mit Schauerenergie
Müonen: Energieverlust ausschliesslich durch Ionisation ( Energieverlust ca. 1.3 GeV
in 1 m Eisen)  grosse Reichweite. Weise Müonen hinter dicken Absorbern nach.
Hadronen: Bleiben im Absorber stecken, bilden ´neue Teilchen (Hadronschauer)
Trennung von pi, K, p: Flugzeit (P<1 10 GeV), Cerenkov Schwellen- und Ringzähler.
Z-Zerfälle: (Beispiele ALEPH Detektor) Wie lassen sich Z- Zerfälle Trennen?
Z-> ee (2 showers in ECAL)
Z-> mu mu (2 penetrating tracks)
Z->tt (slim jets +missing pt)
Zqq ( 2 hadron jets)
Zbb (secondary vertices)
Energiemessung hochenergetischer Elektronen und Hadronen: Welche
Messung gibt die beste Energieaufloesung im Bereich .1 GeV bis 100 GeV?
1.Messung des Impulses im Magnetfeld:
Die Auflösung hängt vom Verhältnis Sagitta/ Genauigkeit des Spurkoordinate in
Ablenkrichtung ab Dp/p ~ p, diese Methode wird also mit zunehmendem Impuls
immer schlechter.
2. Kalorimetrische Messung:
Die Auflösung wird mit der Energie immer besser. Für Sampling Kalorimeter ist die Auflösung
dominiert von der Fluktuation in der Zahl der gemessenen Teilchen im aktiven Detektor.
Dann gilt: DE/E ~ 1/sqrt(E)
Elektromagnetische Schauer (e, gammas):
DE/E = 13%*Sqrt(d/X0)/sqrt(E) [GeV] ; hier ist d die Samplingdicke , X0 die Strahlungslänge
Die kalorimetrische Messung ist typischerweise besser ab ca. 10 –20 GeV.
Hadronische Kalorimeter: die Auflösung ist viel schlechter. Ursache sind a) die ´unsichtbare Energie´
( Neutronen, , Stark ionisierende Teilchen) und b) die Fluktuationen des
Energieanteils der neutralen Pionen. Dies hat die Folge dass das e/p Verhältnis >1 ist d.h. das
Kalorimetersignal (Ladung/GeV, Photonen/GeV etc.) für Pionen kleiner ist als für Elektronen und
Die Auflösung der Energie hadronischer Schauer viel schlechter ist. Typisch gilt: DE/E > 0.35/E ,
wobei die meisten Kalorimeter bei ca. 0.5/E liegen.
Diese Effekte können durch ``Kompensation`` stark reduziert werden.
Relativistische Kinematik: relativistische Effekte in der HEP sind gross!
Wie beeinflusst die relativistische Kinematik
- die mittlere Fluglaenge instabiler Teilchen ?
- die Impulse von Teilchen im Laborsystem bei fixed target Experimenten?
- welche Rolle spielen Lorentzinvariante? Diskutieren sie das am Beispiel eines Streuprozesses
1+2 --> 3+4
Diskussion:
--Fluglängen L instabiler Teilchen werden gross
< L > = c* t *bg = c* t * p/m . Das ermöglicht z.B. Teilchenstrahlen von Pionen, K‘s etc und
Myonenbeschleuniger.
-- Der ‚Lorentzboost‘ vom Schwerpunkts- ins Laborsystem (cmslab) hat drastische Konsequenzen
für die Winkelverteilung der Teilchen und damit auch für die Auslegung der Detektoren insbesondere
für fixed Target Experimente. Pz (lab)= g (b* E(cms) + Pz(cms)) ; g = E/m
-- Streuprozesse sollten möglichst mit Invarianten beschrieben werden. Bei Streuprozessen 22
sind dies insbesondere s= (p1+p3)2 = (E1+E3)2 – (P1+P3)2 = E(cms)2 und
t= (p1-p2)2 = p12+p22 – 2 p1p2 =m12+m22 –(E1E2-P1P2cosq )
(die pi sind Vierervektoren), t= Viererimpulsübertragsquadrat
p1
p2
e
Beispiele: s-Kanal
e+
t-Kanal
e
g
pg 2 =
t=-Q2
S=pg2=E(cms)2
p3
p4
e-
P
p
Energie und Auflösung bei Streuprozessen:wovon hängt die räumliche
Auflösung bei einem Streuprozess ab? Anschauliche Erklärung?
Die räumliche Auflösung Dx bei einem Streuprozess beruht auf der Interferenz von Teilwellen, die von
verschiedenen Orten im Abstand Dx ausgehen und einen Gangunterschied haben, der mindestens der
halben Wellenlänge entspricht damit eine räumliche Struktur erkannt werden kann.
Dies gilt sowohl für das Lichtmikroskop als auch für Hochenergiestreureaktionen. (im Sprachgebrauch
der Optik heisst das, dass neben der 0. Ordnung„im Mikroskop“ mindestens auch die erste Beugungsordnung
registriert wird).
Die Wegdifferenz ist D = 2R sina ; diese soll mindestens 1/2 l = 1/2 h/p sein.
Setzt man R = Dx d.h. wir wollen die Ausdehnung R gerade noch messen dann gilt: Dx= h/(p* sina)
~ hc /E* sina = hc/Q. Hier wurde genutzt p=E/c für relativistische Teilchen .Q ist der Impulsübertrag
der bei HEP reaktionen durch die Invariante Q=sqrt(-t) ersetzt wird..
D
R
Wir brauchen also eine Streuung um einen endlichen
Winkel. Die Auflösung nimmt mit 1/E zu!
In Formeln gilt:
a
Dx= 0.2 eV mm / Q[ev]
Atomphysik/Optik
Dx= 0.2 GeV fm / Q[GeV] HEP
Dabei gilt Q < E(cms)
Beispiel: Um die Ausdehnung des Protons zu sehen (1fm) brauche ich eine Energie von mindestens 0.2 GeV.
Formfaktoren und Strukturfunktionen: Streuung hochenergetischer Elektronen (m,n)
1. elastische Streuung: es gibt nur 2 Invarianten: s=E(cms) konstant für ein Experiment
und
Q2= -t = 4 EE` sin2 Q/2
(E`=Energie des gestreuten Teilchens, Q = Streuwinkel im Labor)
Streung an einem Spin Null Teilchen (Kern mit J=0).
Der Wirkungsqürschnitt für hochenergetische Leptonstreuung ist dann:
ds/dQ2 = 2p a2/Q4 *|F(Q2)|2cos2q/2
Dies ist der Mott-Wirkungsquerschnitt * Formfaktor2 . Der Mottwirkungsqürschnitt für
Elektronstreuung an einen punktförmigen J=0 Teilchen enthält den
wohlbekannten Faktor 1/ sin4 Q/2 des Rutherfordwirkungsqürschnitts, relativistische Korrekturen und
eine Korrektur auf den Spin des Elektrons. Dabei ist F(0)=1 da Q2=0 einer Streuung entspricht bei der
das Elektron in grossem Abstand am Kern vorbeifliegt und jede Ladungsverteilung aus grossem
Abstand betrachtet punktförmig aussieht. F(Q2) ist die Fouriertransformierte der Ladungsverteilung.
Streuung am Nukleon: jetzt kommt auch der Spin des Nukleons und damit sein magnetisches Moment
zum Tragen. Es gibt daher 2 Formfaktoren. (elektrischer und magnetischer FF), beide haben
unterschiedliche Streuwinkelverteilungen und können daher getrennt bestimmt werden.
Inelastische Streuung: e+N--> e+ X ; hier ist X ein hadronischer Endzustand mit Masse MX
Dann gibt es eine weitere Invariante z.B. die Skalenvariable x= (1- (MX2-Mp2)/2Mpn ) , die
für elastische Streuung (MX=Mp) =1 ist und für inelastische Streung zwischen Null und 1 liegt. Sie
misst die ‚Inelastizität‘.
Dementsprechend gibt es 2 Strukturfunktionen F1(x,Q2) und F2(x,Q2) statt der beiden Formfaktoren.
Diese sind a priori beliebig (experimentell zu bestimmen). Bei der tiefinelastischen Streuung (an
Quarks) bekommen sie eine wohldefinierte Bedeutung, dann ist x der Impulsbruchteil des Quarks.
Frage: was sind die wesentlichen Aussagen der elektroschwachen Theorie und wie werden sie
experimentell getestet?
Antworten:
a) es gibt die Vektorbosonen W+,W- und Z0. Deren Massen und Kopplungen an Leptonen, Quarks
und untereinander werden durch einen freien Parameter sin 2qw bestimmt.
Tests: - erzeuge W‘s un Z in ppbar oder e+e- Kollissionen. Es gilt in niedrigster Ordnung:
mW= 37 GeV/ sinqw , mZ=mW/ cosqw .
-- messe Reaktionen die nur über neutrale Ströme gehen und messe deren WQ.
Historisch: nm + e- --> nm + e- und nm + N --> nm + X (tiefinelastische Streuung)
Oder: messe die Selbstkopplung der Vektorbosonen in der Paarerzeugung von W‘s und Z‘s
(γ, Z0-Austausch)
eWe
We
W
g
Z0
n
+
+
NC: epe X
CC: ep ν X
e+
e+
W+
e+
(W-Austausch)
+
W
W+
b) messe die elektroschwache Interferenz:
-- Paritätsverletzung in Atomen (z.B. Cs)
-- Assymmetrie in der Streuung polarisierter Elektronen bei hohen Energien
c) schwache und elektromagnetische WW haben Kopplungen die etwa gleich gross sind. Der Unterschied
liegt nur im Propagator. e = g * sin θW
-- Messe den Wirkungsquerschnitt neutraler und geladener Ströme bei Q2 ~ mW2 ( bei HERA)
Frage: wie sehen die Kopplungen von Z und W‘s an die Leptonen und Quarks aus?
(die schwachen Ladungen)
Antworten:
a) W-Bosonen koppeln universell an Leptonen und Quarks mit der schwachen Ladung g.
Dabei ist jedoch zu beachten, dass bei den Quarks die schwachen Eigenzustände Linearkombinationen
der Masseneigenzustände sind, beschrieben durch die CKM-Matrix.
d‘
Vud Vus
Vub
d
s‘ = Vcd
Vcs
Vcb
s
b‘
Vtd
Vts
Vtb
b
Die Kopplung ist eine reine V-A Kopplung, d.h. die paritätsverletzung ist maximal, Fermionen
koppeln als Linkshänder, Antifermionen als Rechtshänder.
b) der schwache neutrale Strom ist eine Mischung aus dem V-A Strom (3-Komponente des
geladenen Stroms) und dem elektromagnetischen Strom (reiner Vektorstrom)
gL = T3 - qf* sin 2qw für die Vektorkopplungskonstante.Dabei ist qf die Ladung der Fermionen
in Einheiten der Elemenarladung. T3 die Komponente des schwachen Isospins.
gR = qf* sin 2qw Dier rechtshaendige Kopplung ist fuer geladene Fermionen nicht Null!
Neutrinos haben also V-A Kopplung ans Z0 da qn=0, andere haben eine Polarisation die von der
Ladung abhängt.
Diese Kopplungen wurden bei LEP I präzise gemessen und stimmen mit dem SM überein.
Dabei sind die el.schwachen Korrekturen höherer Ordnung wichtig!
Frage: wozu wird das Higgsteilchen im Standardmodell benoetigt?
Welche Eigenschaften hat es?
Was weiss man bisher?
Antworten:
1) das Higgsteilchen wird benoetigt um den Vektorbosonen masse zu geben (Stichwort: spontane
e+
b
Brechung der lokalen Eichsymmetrie)
H
2) es ist ein Teilchen mit Spin 0, das an alle anderen Teilchen proportional zu ihrer Masse koppelt.
Z
3) die Praezisionsmessungen zur elektroschwachen Theorie insbesondere auf dem Z0 sind so genau,
dass sie Korrekturen hoeherer Ordnung erfordern u.a. auch Korrekturen, bei denen ein
Higgsaustauch auftritt. Die Anpassung aller Messungen an die SM Voraussagen ergibt eine
e- bei Massen um 100 GeV. Ohne die Higgsbeitraege
bbar
Higgsmasse mH < 200 GeV mit einer Praeferenz
sind Messungen und SM kaum kompatibel.
~ ln (mH /mZ)
Die direkte Suche nach dem Higgs bei LEP II ergab: mH > 120 GeV.
(hierbei wurde nach der Erzeugung e+e- ==> Z0 H gesucht mit H ==> b bbar ; Z ==> q qbar d.h..
4- jet Ereignissen)
Frage: was sind die wesentlichen Aussagen der QCD und wie werden sie getestet?
Antworten:
a) die starke Wechselwirkung wird durch den Austausch von Gluonen vermittelt, die an alle Teilchen
mit Farbladung koppeln proportional der starken Ladung sqrt( as ). Es gibt eien 3-wertige Farbladung
b) Gluonen haben masse =0, Spin = 1 und sie tragen selber Farbladung! Das heisst es gibt auch die
selbstwechselwirkung der Gluonen.
Der Spin wurde getestet z.B. durch die Winkelverteilungen in 3-jet Ereignissen bei e+e- ==> q qbar g
c) drei Farbladungen sind experimentell nachgewiesen z.B. durch den Wert des hadronischen
Wirkungsquerschnitts in e+e- oder die Verzweigungsverhaeltnisse des W-Bosons.
d) Die Selbstwechselwirkung der Gluonen hat gravierende Auswirkungen:
1. Confinement: - beobachtete Hadronen sind farbneutral, es koennen keine freien quarks existieren.
- das q q Potential steigt fuer grosse Abstaende unbegrenzt an.==> Fragmentation und
Bildung von Jets.
Tests: Potential kann experimentell gemessen werden z.B. im Charmonium und BottoniumSystem. Jets werden exp. beobachtet.
-- die Kopplungskonstante as haengt von einer Skala ab. Sie ist klein fuer kleien Abstaende
bzw. grosse Skalen und waechst unbegrenzt fuer grosse Abstaende bzw. Skalen <<
0.2 fm d.h. fuer Abstaende von der Groesse der Hadronen.
3. Wechselwirkungen zwischen Gluonen sind direkt beobachtbar.
--- gemessen bei 4-Jet Ereignissen in e+e-- bei der 2- Jeterzeugung in Hadronischen Kollissonen
Frage: geben Sie Beispiele fuer harte Streuprozesse an denen Hadronen beteiligt sind.
Warum lassen sich hierfuer QCD Voraussagen einfach machen?
Antworten:
a) harte Prozesse sinnd solche bei denen der ‚Propagator‘ eine grosse Skala s,t,u >> 1 GeV 2 hat.
e
e
u
Q= c,b,t
u
e+
g
Q= c,b,t
+
W
q
p
Tiefinelast. Streuung
t = - Q2 > 1 GeV2
u
Q
ne
d
Erzeugung schwerer Quarks
s = 2* mQ
W-Erzeugung
s = mW
Jets bzw. schwere Quarks
s= 2* mQ oder s>ET2
b) Fuer alle diese Prozesse ist as (s,t) <1 , d.h. Stoerungsrechnung ist moeglich. Die Ergebnisse
entsprechen in niedrigster Ordnung dem Partonmodell
Benoetigt werden hierzu die Impulsverteilungen der Partonen im Hadron, die experimentell
gemessen weren muessen z.B. in der tiefinelastischen Streuung.
d) die Partonverteilungen haengen schwach von der Skala Q ab: Skalenverletzungen.
xu(x,Q2) etc.
Frage: elementare Bindungszustände in der elektromagnetischen und starken
Wechselwirkung
- Wie sehen die Feynmadiagramme für das Positonium und das Charmonium aus (incl Ladungen)- Wie die zugehörigen Potentiale? Was ist gleich, was ist verschieden?
-Wann ist das Feynmandiagram für Charmonium sinnvoll, welchen Teil des Potentials beschreibt es?
- diskutieren Sie Zahl und Quantenzahlen der Bindungszustände.
Antworten:
Positronium
Charmonium
V = m /r
V = c as /r + k*r
m.5
as.5
g
g
m.5
V
as.5
r
Das Feynmandiagramm ist nur
für kleine Kopplungen sinnvoll,
wenn 1-Gluonaustausch dominiert,
d.h. bei kleinem r. das 1/r Potential
kommt von mg = 0
Bei grossem r wird as gross, es werden viele Gluonen
Ausgetauscht und die Selbstwechselwirkung der Gluonen
führt zur Ausbildung eines Farbstrings, der durch das
linear ansteigende Potential näherungsweise beschrieben wird.
Der 3. radial angeregte Zustand (n=3) liegt bereits oberhalb
der DD Schwelle  kein Bindungszustand mehr.