Struktur des Nukleons

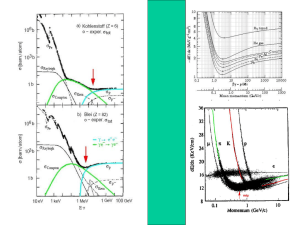
Struktur des Nukleons
Seminar im Bereich der
Kern- und Teilchenphysik
Matthias Böcker
Übersicht
•
•
•
•
•
•
•
•
Streuprozesse und Wirkungsquerschnitte
Formfaktoren
Elastische Elektron-Nukleon-Streuung
Tiefinelastische Streuung, Strukturfunktionen
Das Partonmodell
Das Quarkmodell
Gluonen
Zusammenfassung
Wirkungsquerschnitt
Anschauliche Deutung:
Jedem Streuzentrum wird eine Fläche zugeordnet. Trifft ein
einlaufendes Teilchen diese Fläche, so findet eine Streuung statt
Zahl der Reaktionen  / Streuzentrum Sekunde 

 tot 
Stromdichte j der einfallenden Teilchen
Differentieller Wirkungsquerschnitt:
In der Praxis wird nicht die Gesamtzahl aller Reaktionen registriert,
sondern nur ein geringer Teil der durch den Rumwinkel DW=A/r²
begrenzt wird.
d  Zahl der Reaktionen in dW  / Streuzentrum Sekunde 

dW
Stromdichte j der einfallenden Teilchen
Rutherford-Streuung
Rutherfordsche Streuformel für Streuung eines Elektrons an einem Atomkern:
 Ze2 
2
 d 



2
 d W  Rutherford  4 0   4 E 2 sin 4 2
Nachteil:
In dieser Formel wird jedoch weder der Spin mit einbezogen noch wird die
Reaktionskinematik relativistisch behandelt.
Vorteil:
Rückstoß des Atomkerns ist für kleine Elektronenenergien zu vernachlässigen
E
E' 
1  E / Mc 2  1  cos  
Mott-Wirkungsquerschnitt:
Beschreibung des WQ unter Berücksichtigung des Elektronenspins
 d 


d
W


*
Mott
  v 2 2  
 d 

 1    sin 

2 
 d W  Rutherford   c 
Experimentell:
Bei größerem Impulsübertrag |q| ist der experimentelle WQ der
Elektron-Nukleon-Streuung systematisch kleiner als beim theoretischen
Mott-WQ
Grund:
Bei größerem |q| wird der reduzierte Wellenlänge des virtuellen Photons
kleiner
 Bei genügend großen Energien ‚sieht‘ das gestreute
Elektron nicht mehr die gesamte Ladung des Kerns,
sondern nur noch Teile davon.
 Der Wirkungsquerschnitt nimmt ab.
Beschreibung möglich durch den Formfaktor:
2
 d 
 d 
2

 
  F q 
 d W exp.  d W  Mott
F  q 2    eiqx / f  x  d 3 x
f  x
Herleitung über Fermis
‚Goldene Regel‘
Ladungsverteilung im Kern
1
 iqx /
2
3
 f  r  
F
q

e
d
q
3 
 2 
 
Experimentelle Bestimmung über Fit an den Messdaten
Zusammenhang zwischen radialer Ladungsverteilung
und Formfaktor
Beispiele der Messung von Formfaktoren:
Messung des Formfaktors von 12C durch
Elektronenstreuung.
Gestrichelte Kurve entspricht der Bornschen
Näherung bei einer Welle, die an einer
homogenen Kugel mit diffusem Rand
gestreut wird.
Differentielle WQ an den Kalziumisotopen
40Ca und 48Ca. Zur besseren Darstellung
wurden WQ mit einen Faktor 10 bzw. 10-1
multipliziert. Aus der Lage der Minima
erkennt man, dass der Radius von 48Ca
größer ist als von 40Ca.
=>Die Ladungsverteilung in Kernen ist
homogen, nimmt aber zum Rand hin
exponentiell ab.
Elastische Elektron-Nukleon-Streuung
Größe des Nukleons bestimmt die Energie des eingestrahlten Elektronenstrahls
Experimentell: einige hundert MeV bis zu einigen GeV
Masse des Nukleons: ca. 938MeV
=> Rückstoß des Targets kann nicht mehr unberücksichtigt bleiben
 d 
 d 




d
W
d
W

 Mott 

*
E'

E
Mott
=> Benutzung des Viererimpulsübertrags:
q 2   p  p ' 
2
4 EE '
2 

sin
2
c2
Um nur mit positiven Größen zu arbeiten, definiert man:
Q 2  q 2
Weiteres Problem:
Das Nukleon ist ein Spin-1/2-Teilchen
=>Nukleon hat ein magnetisches Moment:
e
  g

2M 2
=>Zusätzliche WW zwischen Teilchenstrom und magnetischem
Moment des Nukleons.
=>Neben einem elektrischen Formfaktor GE Q 2 braucht
 
 
2
man noch einen magnetischen Formfaktor GM Q .
Der WQ einer elastischen Streuung lässt sich schließlich durch
die ‚Rosenbluth-Formel‘ beschreiben:
2
2
2
2


G
Q


G
Q




E
M
 d   d 

2
2
2



2

G
Q
tan




M

 

2
1
 d W   d W  Mott 

2
Q
mit  
4M 2c 2
  und G  Q 
Bestimmung von GE Q
2
2
M
Für feste Werte von Q2 werden verschiedene Streuwinkel und
damit Strahlenergie gemessen.
Bestimmung von GM
über die Steigung
2
Q
 
 
2
Bestimmung von GE Q
danach über den
Achsenabschnitt bei  = 0
2
2
2
2


G
Q


G
Q




E
M
 d   d 
2
2
2 

 2 GM  Q  tan 2 



1
 d W   d W  Mott 

Für den Grenzfall Q2g0 ergeben sich folgende Werte:
GEp  Q 2  0   1
GEn  Q 2  0   0
GMp  Q 2  0   2,79
GMn  Q 2  0   1,91
aDipolfit
 GEp  Q 2  
mit
GMp  Q 2 
2,79

GMn  Q 2 
1,91
 G Dipol  Q 2 


Q2
Dipol
2
G
 Q   1  0,71 GeV / c 2 

 

2
Berechnung der mittleren quadratischen Radien der Ladungsverteilungen aus Dipolfit möglich:
r2
Dipol
dG Dipol  Q 2 
 6
dQ 2

r
 12
Q 0
a
2
 0,66 fm 2
2
2
Dipol
 0,81 fm
Heutige Ergebnisse der Ladungsradien ergeben für das
Proton einen Wert von
einen Wert von
r2
n
r2
p
 0,862 fm und für das Neutron
 0,10 fm
=>Auch im Neutron müssen sich elektrische geladene
Konstituenten befinden
Tiefinelastische Streuung
Durch Erhöhung der Energie des einfallenden Elektrons
wird die Wellenlänge des virtuellen Photons kleiner und die
Auflösung nimmt zu:
Man könnte eine Unterstruktur des Nukleons erkennen
DResonanz
Nukleonenresonanzen beim Proton lassen darauf schließen,
dass das Proton ein System aus zusammengesetzten
Konstituenten ist.
Feynman-Diagramm der
Proton-D-Resonanz-Anregung
Bei invarienten Massen
W>2,5GeV sieht man keine
Anregungsspektren mehr,
sondern neue stark
wechselwirkende Teilchen
(Hadronen)
Neues Problem:
Bei der inelastischen Streuung kommt neben der Einschussenergie noch die Anregungsenergie des Protons als freier
Parameter hinzu.
Elastische Streuung:
Inelastische Streuung:
W M
2M  Q  0
W>M
2M   Q  0
2
2
Einführung der Strukturfunktionen W1 und W2
Ersetzung der Rosenbluth-Formel
d
 d  
2
2
2 


W
Q
,


2
W
Q
,

tan


1
  2
2
d WdE '  d W  Mott
2

*
Energieübertrag
Mit wachsendem Q2
nehmen die Wirkungsquerschnitte der
Nukleonenresonanzen
sehr rasch ab
Für invariante Massen
W>2GeV sieht man kaum
noch eine Abhängigkeit
von Q²
Im Bereich der tiefinelastischen Streuung hängt die Strukturfunktionen kaum von Q² ab.
Bjorkensche Skalenvariable:
2
Q
x :
2M
Elastische Streuung:
2 M  Q  0
2
=>
x 1
=>
0  x 1
Inelastische Streuung:
2 M  Q  0
2
=> Bjorkensche Skalenvariable ist eine dimensionslose Größe,
die ein Maß für die Inelastizität eines Prozesses ist.
Anstelle der dimensionsbehafteten Strukturfunktionen W1 und
W2 werden dimensionslose Strukturfunktionen verwendet:
F1  x, Q 2   Mc 2W1  Q 2 , 
F2  x, Q 2   W2  Q 2 , 
Großer Bereich
=>Strukturfunktion ist
unabhängig von Q²
=>Das Nukleon besitzt
eine Unterstruktur
aus punktförmigen
Konstituenten!
Die Strukturfunktion F1 rührt von der magnetischen Wechselwirkung her. Für ein Spin-0-Teilchen wäre F1(x)=0 . Für ein
Spin-1/2-Teilchen ergibt sich die so genannte ‚Callan-GrossBeziehung‘:
2xF1  x   F2  x 
Die Callan-GrossBeziehung wird erfüllt.
=> Die punktförmigen
Konstituenten des
Nukleons haben
den Spin 1/2!
Das Partonmodell:
In einem sehr schnell bewegtem System sind die transversalen Impulse der Konstituenten vernachlässigbar
=>Die Elektronen wechselwirken an den Konstituenten wie
bei der elastischen Streuung, wenn die einzelnen Konstituenten nicht untereinander wechselwirken.
Die inelastische ElektronNukleon-Streuung läßt sich auf
eine elastische ElektronParton-Streuung zurückführen.
Nachteil:
Bezugssystem ist
schlecht zu handhaben
Deutung der ‚Bjorkenschen Skalenvariablen‘ x im
Partonmodell:
Die Bjorkensche Skalenvariable entspricht
dem Bruchteil des Viererimpulses des
Protons, der von einem Parton getragen wird.
Gilt jedoch nur in sehr schnell bewegten Systemen!
Lösung:
‚Breit-System‘
Vorteil: Das Photon überträgt keine Energie
Im Breitsystem vereinfacht sich auch die Formel der
Wellenlänge für das Ortsauflösende virtuelle Photon zu:

Q2
=> Q² ist ein Maß der räumlichen Auflösung
Quarkmodell:
Versuch eine Systematik in das System zu bekommen!
1) Nukleon muss mindestens aus drei Quarks bestehen, da
jedes Quark Spin-1/2-Teilchen sind und die Nukleonen
ebenfalls Spin-1/2-Teilchen sind.
2) Mindestens zwei Teilchen , u (up) und d (down) mit der
Ladung +2/3, bzw. -1/3, da Teilchen mit doppelt positiver
Ladung gefunden wurden (D++guuu), aber nur Teilchen mit
einfach negativer Ladung (Dgddd)
Experimentell wurden neben den drei so genannten
Valenzquarks noch andere Teilchen nachgewiesen
=>Es existiert noch ein ‚See‘ aus anderen Teilchen, die aber
nicht an der Quantenzahl des Nukleons beteiligt sind
=>Es existieren noch Quark-Antiquark-Paare im Nukleon,
die als ‚Seequarks‘ bezeichnet werden
Heute sind insgesamt 6 verschiedene Quarks bekannt:
 +2/3 e :
 1/ 3 e :
 u (up ) 
 d ( down ) 


 c ( charm ) 
 s ( strange ) 


 t ( top ) 
 b( bottom ) 


Die Quarks c, t, b sind so schwer, dass sie bei den erreichbaren Werten
für Q² nur eine untergeordnete Rolle spielen und deshalb auch im
folgenden nicht weiter beachtet werden.
Strukturfunktion im Parton-Quark-Modell
Annahme: Das Nukleon besteht aus f verschiedenen
Quarktypen, die jeweils die Ladung zf .e trägt.
g WQ ist proportional zum Quadrat der Ladung, also zf², bei
elektromagnetischer Streuung.
Für ein Quark-Antiquark-System erhält man deshalb:
F2  x   x   z 2f  q f  x   q f  x  
f
q f  x  Quark- und q f  x 
Anti-Quark-Impulsverteilung
4 p
1
1 p

F  x   x    d v  d s  d s    u v  u s  u s    s s  ss  
9
9
9

4 n
1
1 n

e ,n
F2  x   x    d v  d s  d s    uv  us  us    ss  ss  
9
9
9

e, p
2
Formal gehen Proton und Neutron durch Vertauschen von
u- und d-Quark ineinander über (Isospinsymmetrie)
Für ein gemitteltes Nukleon erhält man deshalb:
e ,n
e, p
F
x

F
x



2
2
e, N
F2  x  
2
5
1
 x    q  x   q  x    x   ss  x   ss  x  
18 q u ,d
9
Zweiter Summand nur klein, da s-Quarks nur als Seequarks
vorkommen
=>5/18 ist mittlere quadratische Ladung der u- und d-Quarks
Bei der tiefinelastischen Neutrinostreuung entfallen die Faktoren zf², da hier nur die schwache WW wirkt und bei allen
Quarks gleich ist.
Für die Strukturfunktion erhält man
für die Neutrino-Nukleonstreuung:
F2 , N  x   x    q f  x   q f  x 
f
Experimentell:
Bis auf den Faktor 5/18 sind
die Strukturfunktionen F2e , N
und F2 , N identisch.
=> Die Ladungszahlen +2/3 für das u-Quark und -1/3 für das
d-Quark sind richtig zugeordnet!
Bei Integration über alle mit Verteilungsfunktionen gewichteten
Quarkimpulsen sollte gelten:
1
 F  x  dx  1
N
2
0
Experimentell erhält man:
1
F
 ,N
2
0
1
18 e, N
 x  dx   F2  x  dx  0,5
5 0
=>Die Hälfte des Impulses wird nicht von den Quarks,
sondern von Teilchen, die weder elektromagnetisch noch
schwach wechselwirken getragen.
=>Gluonen
Wie bekommt man eine unterschiedliche Auflösung zwischen
Valenz- und Seequarks hin?
Durch lange WW ist bei kleinen Q² nur die Valenzquarks sichtbar
wo hingegen bei großen Q² Seequarks sichtbar werden.
1/3
Strukturfunktion bei
inelastischer Streuung
Schematische Darstellung
der Strukturfunktion
Interpretation der Partonenimpulsverteilung:
Bei einem Quark bestünde
die Strukturfunktion aus
einen Strich bei 1
Bei drei unabhängigen
Quarks sollte sich die die
Verteilung zu 1/3 hin
verschieben, da sich der
Impuls gleichmäßig verteilt.
Gluonen würden eine
andere Impulsverteilung
hervorrufen und das
Maximum würde sich etwas
verringern. Die Gluonen
selber übernehmen etwa die
Hälfte des Impulses
=>Experimenteller Beweis
der Existenz von einer
‚Suppe‘ aus Quarks,
Anti-Quarks und
Gluonen
Neues Problem:
Spin der einzelnen Quarks beträgt 1/2 und ist gleich dem
Spin des Nukleons.
Experimentell:
D existiert und besteht aus drei u-Quarks
D   uuu
=>Verletzung des Pauli-Prinzips
Lösung: Farbe
Daher Teilchen unterscheidbar und nach außen hin sind alle
Teilchen ‚weiß‘.
Gluonen dienen als Austauschteilchen der Farbe und bestehen
aus Farbe und Antifarbe und sind Träger der starken WW.
Gluonen können in Analogie
zum Positronium ein System
aus Teilchen und
Antiteilchen erzeugen
=>Seequarks entstehen durch Austausch von Gluonen
Innere eines Nukleons
Nachweiß von Gluonen:
Bei einer e--e+-Kollision können Hadronenjets entstehen, die
aus Quark, bzw. Antiquark entstehen.
Es kann aber auch sein, dass neben den beiden Quark
zusätzlich ein Gluon entsteht (Analogie zur Bremsstrahlung).
Zusammenfassung:
• Die Ladungsverteilung bei Kernen entspricht einer
homogenen Verteilung mit diffusem Rand.
• Die Ladungsverteilung im Proton lässt sich durch eine
e-Funktion beschreiben
• Ein Nukleon ist aus drei punktförmigen Valenzquarks
aufgebaut, die jeweils den Spin ½ tragen.
• Die Valenzquarks tragen nur etwa 50% des Impulses des
Nukleons. Die anderen 50% werden von den Gluonen, den
Austauschteilchen der starken WW getragen.
• Quarks tragen eine Farbe, Nukleonen sind aber nach außen
immer ‚weiß‘
• Neben den Valenzquarks existieren noch Seequarks, die als
virtuelle Quark-Antiquarkpaare aus den Gluonen
hervorgehen.