AC I (AC) – HS 2011 – Übungen + Lösungen – Serie 10

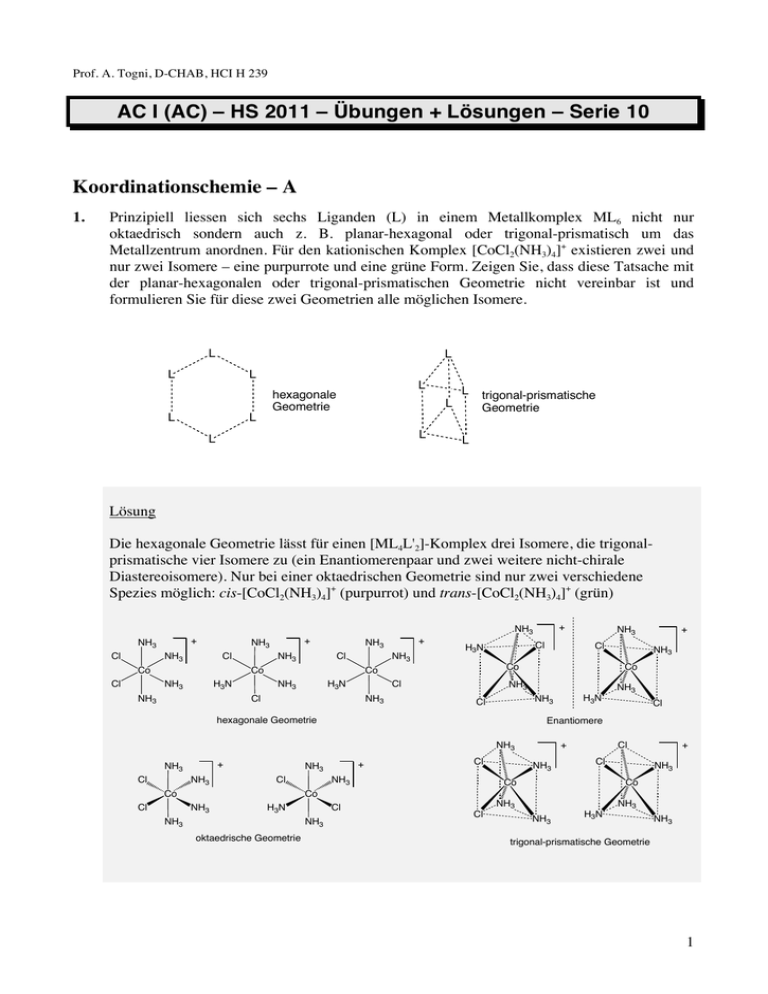
Prof. A. Togni, D-CHAB, HCI H 239
AC I (AC) – HS 2011 – Übungen + Lösungen – Serie 10
Koordinationschemie – A
1.
Prinzipiell liessen sich sechs Liganden (L) in einem Metallkomplex ML6 nicht nur
oktaedrisch sondern auch z. B. planar-hexagonal oder trigonal-prismatisch um das
Metallzentrum anordnen. Für den kationischen Komplex [CoCl2(NH3)4]+ existieren zwei und
nur zwei Isomere – eine purpurrote und eine grüne Form. Zeigen Sie, dass diese Tatsache mit
der planar-hexagonalen oder trigonal-prismatischen Geometrie nicht vereinbar ist und
formulieren Sie für diese zwei Geometrien alle möglichen Isomere.
L
L
L
L
L
L
hexagonale
Geometrie
L
L
L
L
L
trigonal-prismatische
Geometrie
L
Lösung
Die hexagonale Geometrie lässt für einen [ML4L'2]-Komplex drei Isomere, die trigonalprismatische vier Isomere zu (ein Enantiomerenpaar und zwei weitere nicht-chirale
Diastereoisomere). Nur bei einer oktaedrischen Geometrie sind nur zwei verschiedene
Spezies möglich: cis-[CoCl2(NH3)4]+ (purpurrot) und trans-[CoCl2(NH3)4]+ (grün)
+
NH3
+
NH3
Cl
NH3
Cl
NH3
H3N
Co
Cl
+
NH3
NH3
Cl
NH3
H3N
NH3
Co
NH3
+
NH3
Cl
NH3
Cl
Co
Co
Cl
Cl
H3N
NH3
+
NH3
NH3
Co
Cl
+
NH3
Cl
Cl
Enantiomere
+
NH3
Cl
H3N
NH3
hexagonale Geometrie
NH3
Co
NH3
Cl
+
NH3
Cl
NH3
NH3
+
Cl
Cl
Co
NH3
Co
Co
NH3
H3N
NH3
Cl
NH3
oktaedrische Geometrie
NH3
Cl
NH3
NH3
H3N
NH3
trigonal-prismatische Geometrie
1
2.
Die zwei Ionen A und B weisen eine oktaedrische Geometrie an den Zentralatomen Co bzw.
P auf.
A und B, ein Kation und ein Anion, können ein Salz der Zusammensetzung AB bilden.
Wieviele solche Salze gibt es und in welcher stereochemischen Beziehung stehen sie jeweils
zueinander?
–
O
+
H2N
O
O
NH2
O
O
Co
O
O
P
NH2
O
O
H2N
O
A
B
Lösung
Die zwei Ionen sind chiral. Damit existieren je zwei enantiomere Formen, A und A' bzw. B
und B'.
Wenn ein Salz AB gebildet wird, ergeben sich vier Kombinationen, d.h. zwei diastereomere
Enantiomerenpaare: AB und A'B' bzw. AB' und A'B sind enantiomer. Merke die Analogie
zur Situation eines organischen Moleküls mit zwei unabhängigen, konstitutionell
unterschiedlichen, stereogenen Zentren.
O
+
H 2N
O
NH2
Co
O
O
+
NH2
NH2
O
O
Co
NH2
NH2
H 2N
O
O
NH2
A: chiral, 2 Enantiomere möglich (A und A')
–
–
O
O
O
O
P
O
O
O
P
O
O
O
O
O
B: chiral, 2 Enantiomere möglich (B und B')
3.
Verbindung 1 verhält sich als tetradentater Ligand.
a) Machen Sie Aussagen über die Struktur der Komplexe mit der
Zusammensetzung [CuCl(1)]+ (2), [FeCl2(1)] (3), [(Cu(1))2Br]+ (4),
und [(FeF(1))2O]2+ (5), und geben Sie die Oxidationsstufe der
Metallzentren an.
b) Gibt es bei diesen Komplexen mögliche Isomere? Können sie chiral
sein? Warum?
N
N
N
N
1
2
Lösung
Komplex [2]+ zeigt eine trigonal-bipyramidale Geometrie mit dem zentralen
Aminstickstoffatom des Liganden und dem Chloroliganden in axialer Position. Eine
prinzipiell denkbare aber nicht beobachtete isomere Form hätte den Chloroliganden trans zu
einem Pyridinylstickstoffatom. Das wäre aber eine stark verzerrte Struktur (keine 120°Winkel in der Ebene der trigonalen Pyramide möglich).
+
N
N
N Cu
N
N Cu
N
Cl
+
N
N
Cl
2, Cu(+II), trigonal bipyramidal
Die Abbildung zeigt die Struktur des Kations 2 in Kristallen von [2]PF6 (siehe K. D. Karlin et
al., Inorg. Chem. 1982, 21, 4106).
Durch das Molekülion können drei Spiegelebenen gelegt werden. Diese Ebenen werden durch
das Aminstickstoffatom, das Kupferatom und eines der drei Pyridinylstickstoffatome
definiert. Das Vorhandensein von molekülinternen Spiegelebenen bedeutet, dass das Molekül
nicht chiral ist.
Komplex [3] nimmt eine oktaedrische
N
Geometrie an. Die zwei Chloroliganden
N
N
können nur cis zueinander stehen. Auch
N Fe Cl
dieses Molekül ist achiral. Die einzige
Cl
interne Spiegelebene wird durch das
Eisenatom, die zwei Chloratome und zwei 3, Fe(+II), oktaedrisch
trans-ständigen Stickstoffatome definiert.
(Abgebildete Kristallstruktur: D. Mandon et al., Inorg. Chem. 2002, 41, 5364)
Bei Komplex [4]+ liegt eine sehr ähnliche strukturelle Situation vor, wie bei [2]+. Zwei
identische spiegelsymmetrische Cu(1)-Einheiten teilen sich einen verbrückenden
Bromoliganden. Die Kristallstruktur des Salzes [4]BPh4 zeigt, dass die Cu-Br-Cu-Einheit
gewinkelt ist (117.5°, siehe W. T. Eckenhoff, T. Pintauer, Inorg. Chem. 2010, 49, 10617).
Durch Rotation um die Cu–Br-Bindungen sind Konformationen zugänglich, die den ganzen
Komplex spiegelsymmetrisch, d.h. achiral machen.
+
N
N
N Cu
N
Br
N
N
Cu N
N
4, Cu(+I), trigonal bipyramidal, µ2-Br
3
Komplex [5]2+ hat strukturelle Gemeinsamkeiten
mit [3] und [4]+. Er zeigt eine oktaedrische
Geometrie an den zwei Fe(+III)-Zentren und enthält
einen verbrückenden Oxoliganden (O2–). Die
Atome O und F stehen jeweils cis zueinander,
können aber innerhalb einer Einheit in ihrer
Position gegeneinander vertauscht werden. Das
ergibt drei mögliche Isomere mit dem
Oxoliganden trans zum Aminstickstoffatom oder
trans zu einem Pyridinylstickstoffatom. Die drei
Möglichkeiten können in diesem Sinne als
(trans,trans), (cis,cis), (trans,cis) und (cis,trans)
bezeichnet werden, wobei die Isomere (trans,cis)
und (cis,trans) äquivalent sind. Jede FeF(1)Einheit ist spiegelsymmetrisch. In Analogie zu
Komplex [4]+ sind auch hier Konformationen
zugänglich, die gesamtspiegelsymmetrisch sind, also auch achiral.
In der Kristallstruktur von [5](BF4)2 findet man nur die (trans,cis)-Form, die eine nahezu
lineare Fe–O–Fe-Einheit mit einem Fe-O-Fe-Winkel von 176.1° aufweist (siehe K. S. Min et
al., Inorg. Chim. Acta 2007, 360, 1854). Die abgebildete statische Konformation des
Molekülions 52+ im Kristall kann zwar als achiral angesehen werden, eine Drehung um eine
Fe–O-Bindung würde aber die einzige interne Spiegelebene durch F-Fe-O-Fe-F aufheben und
somit eine chirale Struktur ergeben.
4.
Welche Komplexe sind chiral?
CH3 –
H3C
Re
ON
OC
PPh3
Cl
I
OC
1
Anmerkung:
Fe
O
Fe
Li
O
Br
O
Ph
2
M
O
CH3
Ph
3
4
bedeutet M(η5-C5H5), siehe Folie 7, Komplexe
Lösung
1 ist chiral, das Re-Atom ist stereogen, analog zu einem stereogenen Kohlenstoffatom. Die
vier verschiedenen Liganden sind tetraedrisch angeordnet.
2 ist nicht chiral, obwohl die vier Liganden tetraedrisch angeordnet sind, wie in 1. Zwei sind
allerdings identisch (CO). Eine interne Spiegelebene wird durch die Atome Fe, I und das
Zentrum des Cp-Liganden definiert.
3 ist chiral, es enthält keine interne Spiegelebene. Strukturell verhält sich dieser Komplex wie
eine organische spiro-Verbindung.
4
4 ist chiral. Auch hier ist keine interne Spiegelebene vorhanden. Man spricht bei solchen 1,2disubstituierten Ferrocenen von “planar-chiralen” Verbindungen.
5.
Bei Platin in der Oxidationsstufe 0 lassen sich mit Phosphinliganden Komplexe herstellen und
isolieren, die unterschiedliche Koordinationszahlen (KZ) aufweisen. Tricyclohexylphosphin
(PCy3), Triethylphosphin (PEt3) und Trimethylphosphin (PMe3) bilden die Komplexe
[Pt(PCy3)2] (1), [Pt(PEt3)3] (2) und [Pt(PMe3)4] (3). Erklären Sie, warum die verschiedenen
Phosphine zu verschiedenen bevorzugten KZ führen und machen Sie Aussagen über die
Geometrie der Komplexe 1-3.
Lösung
Die verschiedenen bevorzugten Koordinationszahlen bei Pt(0)-Komplexen mit
Phosphinliganden sind auf den sterischen Anspruch (Grösse) der Ligaden zurückzuführen.
Der sterische Anspruch nimmt hier von PCy3 zu PEt3 zu PMe3 ab. Entsprechend kann die
Koordinationszahl zunehmen.
1 ist linear (Winkel(P-Pt-P) = 180°).
2 ist trigonal planar (Winkel(P-Pt-P) = 120°).
3 ist tetraedrisch.
5