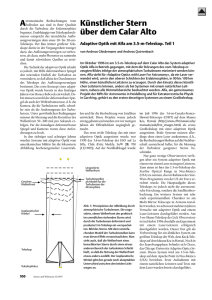
α = λ D [Radian1

Skript zum Versuch F36 Teil II
„Wellenfrontanalyse mit einem Shack-Hartmann-Sensor“
des Fortgeschrittenen-Praktikums II der Universität Heidelberg für Physiker
Aufbau eines Shack-Hartmann Wellenfrontsensors. Messung einfacher optischer
Aberrationen. Wellenfrontrekonstruktion mit Hilfe von Zernike-Funktionen.
Heidelberg, Oktober 2006
Dr. Stefan Hippler, Dr. Wolfgang Brandner, Prof. Dr. Thomas Henning
Einleitung und Motivation: Der Einfluss der Atmosphäre auf die Bildqualität
eines Teleskops
Betrachtet man den Sternenhimmel mit dem bloßen Auge, so fällt in erster Linie das Funkeln der
Sterne, die Szintillation, auf. Dieser Effekt wird durch die atmosphärischen Turbulenzen verursacht,
die dafür sorgen, dass ständig kalte und warme Luftschichten vermischt werden. Die
Temperaturabhängigkeit des Brechungsindexes der Luft führt zu einer, wenn auch sehr schwachen,
optischen Inhomogenität. Dadurch zerfällt die Atmosphäre in viele zufällig verteilte Turbulenzzellen
mit Durchmessern von 10 bis 20 cm, die wie schwache Linsen wirken. Durch ihre lichtsammelnde
Wirkung sorgen sie in Bodennähe für Intensitätsschwankungen über Bereiche von einigen Zentimetern.
Beim Beobachten mit einem Teleskop von mehreren Metern Durchmesser machen sich die
Turbulenzen weniger durch Intensitätsschwankungen als durch die granulationsartige Struktur
(Speckles) der Bilder von Einzelsternen störend bemerkbar. Da von der Teleskopapertur viele dieser
Turbulenzzellen gleichzeitig erfasst werden, zersplittert das Bild in viele zufällig verteilte Einzelbilder,
die Speckles. Die Zahl der Speckles entspricht ungefähr der Anzahl der Turbulenzzellen in der
Teleskopapertur, und die Größe des verspecklelten Sternbildes beträgt unter guten atmosphärischen
Bedingungen ungefähr eine Bogensekunde.
Die Form und die Lage der Specklebilder ändern sich in Abhängigkeit davon, wie schnell die
Turbulenzen vor der Teleskopapertur vorbeiziehen. Im Allgemeinen muss die Belichtungszeit kleiner
als 1/10 Sekunde sein, um ein „scharfes“ Specklebild zu sehen. Werden mehrere Aufnahmen mit
kurzer Belichtungszeit wie in einem Film aneinandergereiht, so sieht man die zeitliche Veränderung
der Turbulenzen als „Wimmelbewegung“ der einzelnen Speckles und als seitliches Hin- und
Herwandern des Sternbildes. Bei Belichtungszeiten von einigen Sekunden tragen beide Effekte zum
Verschmieren des Specklebildes bei, und es entsteht ein gleichmäßig ausgeleuchtetes Bildscheibchen,
dessen Halbwertsbreite (englisch: Full Width Half Maximum, FWHM) in der Fachsprache als Seeing
bezeichnet wird. Je nach Beobachtungsstandort und meteorologischen Bedingungen beträgt das Seeing
0.5 bis 2.5 Bogensekunden.
Die Definition des Auflösungsvermögens eines Teleskops kann verwendet werden, um einen
Zusammenhang zwischen dem Seeing und der Größe der Turbulenzzellen herzustellen. Es ist
"=
#
[Radian]
D
das beugungsbegrenzte Auflösungsvermögen eines Teleskops mit dem Durchmesser D bei der
Wellenlänge λ. Im Sichtbaren, bei einer Wellenlänge von 500 nm, hat z.B. ein 3.5-m-Teleskop ein
theoretisches Auflösungsvermögen von 1.43E-7 rad oder ca. 0.03 Bogensekunden, d.h. zwei
punktförmige Sterne, die 0.03 Bogensekunden voneinander entfernt sind, könnten gerade noch als
Einzelsterne wahrgenommen
! werden. Das durch das Seeing begrenzte Auflösungsvermögen von 1
Bogensekunde entspricht einem fiktiven Teleskopdurchmesser von 10 cm; das ist gerade die Größe der
Turbulenzzellen.
Im Rahmen der Beschreibung der Turbulenz als statistischem Phänomen spricht man anstatt von
Turbulenzzellen von der Korrelationslänge r0, die nach einem amerikanischen Physiker auch FriedParameter genannt wird. Diese Größe bezeichnet den Durchmesser der Wellenfront, über den die
Wellenfrontstörung, d.h. die Abweichung von der ebenen Welle, vernachlässigbar
(Standardabweichung < 1 rad) ist. Daher ist das anschauliche Bild von Turbulenzzellen mit dem
Skript zum Versuch F36 Teil II
Seite 2 von 6
Durchmesser r0, innerhalb derer sich das Licht ungestört ausbreiten kann, durchaus zutreffend. Je
größer die Korrelationslänge wird, je mehr sich also r0 dem Teleskopdurchmesser D annähert, desto
näher kommt das Auflösungsvermögen der Beugungsgrenze " .
Die Wellenfront kann man sich als von den Turbulenzen geschaffene Berg- und Tallandschaft
vorstellen, deren typischer Höhenunterschied wellenlängenunabängig im Bereich von 3-6 µm liegt.
Für die Bildqualität relevant ist das Verhältnis der Abweichung der Wellenfront
von der ebenen Welle
!
zur Beobachtungswellenlänge; ein Zahlenwert von 3-6 µm ist zum Beispiel bei einer Wellenlänge von
10 µm ein relativ unbedeutender Wert von 0.3 bis 0.6 Wellenlängen; im Sichtbaren bei einer
Wellenlänge von 0.5 µm dagegen beträgt die Abweichung 6-12 Wellenlängen. Eine Formel für die
Korrelationslänge r0 beschreibt diesen Effekt quantitativ. Es gilt r0 ~ λ6/5, d.h. der Bereich, über den die
Wellenfrontstörung vernachlässigbar ist, wächst mit der Wellenlänge. Ein r0 von typischerweise 10 cm
bei 0.5 µm ist dann gleich bedeutend mit einem r0 von 360 cm bei 10 µm!
Die Specklebilder bei 0.5 µm und bei 10 µm sehen dementsprechend bei identischen atmosphärischen
Bedingungen völlig verschieden aus (siehe Abbildung 1). An einem 3.5-m-Teleskop hat man im
Sichtbaren bei 0.5 µm eine Wolke von (D/r0)2 ≈ 1000 Speckles, die sich in einer wilden
Wimmelbewegung befinden und deren Einhüllende eine Halbwertsbreite von 1 Bogensekunde hat.
Jedes Speckle hat die Größe des Beugungsscheibchen des Teleskops, also 0.036 Bogensekunden. Im
Infraroten bei 10 µm gibt es dagegen nur ein einziges Speckle mit einer Halbwertsbreite von 0.6
Bogensekunden, der Größe des Beugungsscheibchens bei 10 µm, da r0 größer als der
Teleskopdurchmesser D ist. Der einzige Effekt der Turbulenz besteht darin, dass das Bild relativ
langsam hin- und herwandert.
Abbildung 1: Für identische atmosphärische Bedingungen an einem 3.5-m-Teleskop
simulierte Sternbilder bei 0.5 µm (links) und bei 10 µm (rechts). Während bei 0.5 µm ein
Specklebild mit ungefähr 1000 Einzelspeckles und einer Einhüllenden von einer
Bogensekunde vorliegt, sieht man bei 10 µm jetzt schon das Beugungsscheibchen mit nur
leicht deformierten Beugungsringen.
Anhand dieses Zahlenbeispiels bekommt man bereits einen Eindruck davon, wie verschieden die
Anforderungen an eine adaptive Optik (AO) bei 0.5 µm und bei 10 µm sind. Während es bei 10 µm
ausreicht, die Bildbewegung einzufrieren, um ein beugungsbegrenztes Bild zu erzeugen, müssen bei
0.5 µm alle 1000 Speckles mit Hilfe eines deformierbaren Spiegels in einem einzigen
Beugungsscheibchen vereint werden, um die physikalisch mögliche Abbildungsleistung des Teleskops
zu erreichen. Wegen der technischen Anforderungen an ein adaptives Optik-System im sichtbaren
Spektralbereich beschränkt man sich meist darauf, im nahen Infraroten bei 1-2 µm zu beobachten, wo
mit der kleineren Zahl von 50-200 Speckles auch die Anforderungen geringer sind.
2
Skript zum Versuch F36 Teil II
Seite 3 von 6
Wellenfronten Messen und Korrigieren: Die Komponenten einer Adaptiven
Optik
Eine Adaptive Optik enthält in der Regel einen Tip/tilt Spiegel und einen verformbaren/deformierbaren
Spiegel (deformable mirror), welche die atmosphärischen Wellenfrontdeformationen fortwährend
ausgleichen. Die verbleibenden Deformationen werden mit einem Wellenfrontsensor (wavefront
sensor) gemessen. Eine Regelkreis-Elektronik (control system, real-time computer) setzt die Signale
des Wellenfrontsensors in Steuersignale für das aktive Element um. Ein Teil des Lichts wird
ausgekoppelt und der Beobachtung zugeführt, was in der Regel eine Infrarot-Kamera ist.
Abbildung 2 zeigt ein Schema eines Adaptiven Optik Systems in der Astronomie und deren
Komponenten. Es gibt eine Reihe von Methoden, um diese Störungen zu messen. Die am weitesten
verbreiteten in der Astronomie sind "Curvature wavefront sensing" und die Wellenfrontanalyse nach
dem Shack-Hartmann Prinzip.
Abbildung 2: Schematische Darstellung einer Adaptiven Optik in der Astronomie
Wellenfrontmessungen mit dem Shack-Hartmann-Sensor
Das Shack-Hartmann Prinzip soll nun kurz hier erläutert werden. Die Öffnung eines Teleskops wird
mittels einer Mikro-Linsen-Maske in Unteraperturen (Subaperturen) unterteilt. In jeder Subapertur wird
die relative Position eines Sterns - und somit die lokale Wellenfront-Verkippung - gemessen. Hieraus
lässt sich die Deformation der Lichtwelle bestimmen.
Eine Anordnung von Mikrolinsen unterteilt die Apertur des zu messenden Lichtstrahls in Subaperturen.
Jede Linse erzeugt einen Fokalpunkt im Abstand der Fokallänge der Linse. Bei einer lokalen
Verkippung der Wellenfront innerhalb der Subapertur erfolgt eine Verschiebung des Fokalpunktes aus
der Position x1 nach x2 um den Betrag !x . In erster Näherung ist diese Verschiebung genau
proportional der Verkippung der Wellenfront innerhalb der Linse.
3
Skript zum Versuch F36 Teil II
Seite 4 von 6
Abb. 3 zeigt diese Verschiebung. Ein Shack-Hartmann-Wellenfrontsensor erfasst diese Verschiebung
und schließt dadurch auf das Maß der Verkippung der Wellenfront innerhalb der Linse. Nach
entsprechender Detektion einer zweidimensionalen Matrix von Fokalpunkt-Verschiebungen kann die
komplette Wellenfront rekonstruiert werden. Mögliche Fehler bei der Rekonstruktion der WellenfrontVerkippung innerhalb einer Linse entstehen dabei durch die Unsicherheiten in der Bestimmung der
Fokalpunkt-Verschiebung. Die Bestimmung der Verschiebung wird im Folgenden genauer betrachtet.
Abbildung 3: Schematische Darstellung des Shack-Hartmann Messprinzips
Nach den Vereinfachungen der Paraxial-Optik kann der folgende eindimensionale Zusammenhang
definiert werden:
"x = f#
Dabei ist " der Kippwinkel in Radian (tilt) der Wellenfront über eine Mikro-Linse, !x die
Verschiebung des Fokalpunkts auf dem CCD-Detektor (Gradient). Im Praktikumsversuch sitzt
zwischen dem Linsenarray mit der Brennweite f=45mm noch eine so genannte Relay-Optik (Apo!
Rodagon-N f/2.8 mit 50mm Brennweite),
welche die Brennebene der Mikrolinsen auf den CCD!Detektor abbildet und dabei zusätzlich eine optische Vergrößerung / Verkleinerung M bewirkt. Das im
Praktikum verwendete Mikrolinsenarray hat einen Durchmesser von 5mm und besitzt 28 Mikrolinsen,
die in zwei Ringen (Keystone Anordnung) angeordnet sind. Der horizontale Abstand zweier
benachbarter Mikrolinsen beträgt ca. dsub=714µm ist also in etwa gleich dem Durchmesser einer
Subapertur. Ein Pixel des CCD-Detektors hat eine Größe von 6.7µm x 6.7µm. Mit diesen Angaben
kann die Vergrößerung M der Optik bestimmt werden. Für die optische Weglängendifferenz OPD gilt:
OPD = "dsub
Damit ergibt sich im eindimensionalen Fall ein einfacher Zusammenhang zwischen der Messgröße des
Shack-Hartmann-Sensors, dem Gradienten (Slope) !x , und der Steigung der Wellenfront über die
Subapertur bzw. der optischen Weglängendifferenz OPD in Einheiten der benutzten Wellenlänge "
!
zu:
"x =
f # M # $ # OPD
dsub
!
Der Shack-Hartmann-Sensor verwendet zur Rekonstruktion der Wellenfront mehrere Linsen, die in der
Regel äquidistant in einer zweidimensionalen lateralen Anordnung im Detektor-Strahlengang
angebracht werden. Dieses!
Linsenarray erzeugt eine Matrix von Fokalpunkten. Die Verschiebung jedes
Fokalpunkts ist ein Maß für die Verkippung der Wellenfront innerhalb der zugehörigen Linse, und aus
den Messungen der einzelnen Verschiebungen lässt sich anhand eines Näherungsalgorithmus die
gesamte Wellenfront annähern.
4
Skript zum Versuch F36 Teil II
Seite 5 von 6
Zur Detektion der Abbildungen eines Shack-Hartmann Linsenarrays setzt man meist eine CCD ein. Für
die Detektion der Aufnahme jeder einzelnen Subapertur benötigt man einen quadratischen Ausschnitt
von mindestens 2 x 2 Pixeln. Um optische Übersprechen (engl. Crosstalk) zwischen den Subaperturen
zu vermeiden, wird zwischen die Subaperturen ein Sicherheitsabstand von mindestens ein Pixel Breite
eingebracht. Nach diesem Prinzip arbeiten manche Shack-Hartmann-Systeme mit 3 x 3 Pixeln pro
Subapertur. Eine gängige Alternative sind 4 x 4 bis 8 x 8 Pixel pro Subapertur (z.B. Starfire Optical
Range, Adaptive Optik des Calar Alto ALFA Systems).
Je größer die Pixelzahl, desto dynamischer ist der Wellenfrontsensor (d.h. stärkere Verkippungen
können gemessen werden) und die Objekte dürfen eine größere Ausdehnung besitzen. Jedoch ist dies
mit stärkerem Rauschen verbunden, weil die Anzahl der auszulesenden Pixel und die Auslesezeit
zunehmen. Zur Steigerung der Auslesegeschwindigkeit und Verringerung des Ausleserauschens
können die 8 x 8 Pixel zu so genannten Superpixel "gebinnt" werden, wodurch man eine geringere Zahl
von (größeren) Pixeln simuliert.
Von Shack-Hartmann-Gradienten zu Wellenfronten
Wie aus der vorhergegangenen Beschreibung hervorgeht, kann man für jede Subapertur I, die mittleren
Weglängendifferenzen bestimmen durch
dsub "x i
d "y
= OPDx i und sub i = OPDy i ,
fM#
fM#
und aus diesen Informationen die Wellenfront über die gesamte Mikrolinsenmaske rekonstruieren.
Im allgemeinen kann eine Wellenfront als eine Summe Polynome höherer Ordnung mit jeweiligen
Koeffizienten repräsentiert werden. Eine in der Optik häufig verwendete Darstellung wurde von F.
!
Zernike 1934 !
zur Beschreibung der Qualität
von Hohlspiegeln entwickelt. Die Zernike-Polynome
besitzen Orthogonalität und den typischen Formen von Aberrationen wie zum Beispiel Z4=Defokus,
Z5=Astigmatismus, Z7 =Koma und sphärische Aberrationen lassen sich dedizierte Koeffizienten
zuordnen (siehe Tabelle 1.1). Zernike beschreibt eine Wellenfront W(x,y) als Summe aus den
Produkten dieser Polynome Zn(x,y) mit den Koeffizienten Cn
W ( x, y ) =
"
!C Z
n
n
( x, y ) .
0
Mit:
Tabelle 1: Einige Zernike Polynome in kartesischen Koordinaten.
5
Skript zum Versuch F36 Teil II
Seite 6 von 6
Versuchsdurchführung und Messungen
Im Rahmen des F-Praktikums sollen folgende Aufbauten und Messungen durchgeführt werden:
1.
2.
3.
4.
5.
Aufbau eines Shack-Hartmann-Sensors aus den zur Verfügung gestellten Einzelkomponenten
auf einer optischen Bank.
Aufnahmen von Shack-Hartmann Bildern (Shack-Hartmann Spot Images) mit einer
Laserlichtquelle.
Auffinden des besten Fokus als Funktion der Position der Relay-Optik auf der optischen
Bank.
Messung von Shack-Hartmann Gradienten für verschiedene optische Aberrationen.
Bestimmung einer Wellenfront aus den Messdaten (Shack-Hartmann Gradientenbild).
Für die lange Auswertung zusätzlich:
6.
7.
Rekonstruktion von Wellenfronten mit Hilfe der Zernike Polynome (Modenrekonstruktion,
modal reconstruction).
Alternativ zu Punkt 6: Lokale Rekonstruktion der Wellenfronten mit Hilfe eines geeigneten
2D Oberflächenfits.
Beispiel einer Shack-Hartmann-Aufnahme.
6