E. SUPRALEITUNG 1. Grundlagen Einige Elemente und

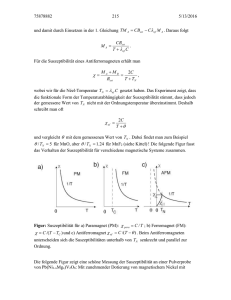
Friedrich-Alexander-Universität Erlangen-Nürnberg
Institut für Werkstoffwissenschaften 6 / AlN
Martensstr. 7, 91058 Erlangen
Vorlesung Grundlagen der WET I
Dr.-Ing. Matthias Bickermann, Prof. Dr. A. Winnacker
E. SUPRALEITUNG
1. Grundlagen
Einige Elemente und Verbindungen besitzen (teilweise auch abhängig von ihrer Kristallstruktur) unterhalb einer Sprungtemperatur TC keinen elektrischen Widerstand
mehr. Es handelt sich um einen Phasenübergang zweiter Ordnung ohne Änderung in
der Kristallstruktur, aber z.B. mit sprunghafter Änderung der spezifischen Wärme.
[Bild 1] [Bild 2] [Bild 3]
In der supraleitenden Phase verdrängt das Material jedes Magnetfeld (MeissnerOchsenfeld-Effekt; M = – H), es kann also als idealer Diamagnet betrachtet werden.
Da es Energie kostet, das Magnetfeld abzuschirmen, kann der Supraleiter nur ein
(temperaturabhängiges) begrenztes Magnetfeld HC(T) abschirmen, ohne in den nor⎡ ⎛ T ⎞2 ⎤
malleitenden Zustand überzugehen. Es gilt: H C (T ) = H C (0 K ) ⋅ ⎢1 − ⎜⎜ ⎟⎟ ⎥ . Insbeson⎢⎣ ⎝ TC ⎠ ⎥⎦
dere gilt H C (TC ) = 0 . [Bild 4] [Bild 5]
Man kann zeigen, dass das Magnetfeld an der Oberfläche des Supraleiters eindringen kann, allerdings nimmt es mit zunehmender Tiefe exponentiell ab: B = B0 e
−
x
ΛL
m
(m ist die Masse, n die Dichte der supraμ0 n e 2
leitenden Elektronen). In dieser Randzone baut sich der Supra-Ringstrom auf, der
das Magnetfeld abschirmt. Über H C = Λ L j C lässt sich damit auch die kritische
Stromdichte jC(T) bestimmen, die der Supraleiter maximal tragen kann. [Bild 6]
mit der London-Eindringtiefe Λ L =
Die freie Energie F eines supraleitenden Systems gegenüber dem normalleitenden
System beträgt F = V ⋅ w = V ∫ B ⋅ dH = ½ μ 0 H C2 (T ) V wegen BC = µ0 (HC + M) = 0; V
ist das Kristallvolumen. Es gilt F(TC) = 0, d.h. oberhalb von TC ist der supraleitende
Zustand energetisch ungünstiger.
2. BCS-Theorie
In der BCS-Theorie (Bardeen, Cooper, Schrieffer 1959) wird die Supraleitung durch
eine anziehende Wechselwirkung zwischen zwei freien Elektronen erklärt. Das erste
Elektron hinterlässt beim "Vorbeiflug" eine Gitterdeformation, die anziehend auf ein
weiteres Elektron wirkt. Dadurch bilden sie ein Zweielektronensystem, ein CooperPaar. Die Gitterdeformation wird als ständige Emission und Absorption von virtuellen
Phononen beschrieben, die Aufgrund der Energieerhaltung jeweils nur innerhalb der
Unschärferelation existieren. Durch den Phononenaustausch wechseln die beiden
Elektronen ständig ihre Wellenzahlvektoren k1 und k2, wobei die Summe jeweils
konstant bleiben muss. Man kann zeigen, dass die Elektronen eines Cooperpaar
entgegengesetze Wellenzahlvektoren und Spins haben: (k ↑; − k ↓ ) . [Bild 7]
Schon aus der Elektronengeschwindigkeit (ca. 108 m/s) und der maximalen Phononenfrequenz (ca. 1013 Hz) kann man schließen, dass die Elektronen ca. 100 nm voneinander entfernt sind und deshalb auch keine Coulomb-Abstoßung spüren. Man
beachte, dass in diesen 100 nm durchaus noch weitere (durchaus z.B. 107) CooperPaare befinden!
Cooperpaare gehorchen durch ihren Gesamtspin Null nicht dem Pauli-Prinzip, sondern haben alle die gleiche Energie (Bose-Statistik), die bei T = 0 K gleich der FermiEnergie ist. Diese Energie liegt um einen Wert Δ ("Bandlücke des Supraleiters") unterhalb der möglichen Energiezustände einzelner Elektronen. Es benötigt also die
Energie 2Δ, um ein Cooperpaar aufzubrechen. Die Zustandsdichte der angeregten
(einzelnen, normalleitenden) Elektronen besitzt einen Pol für E = Δ und lässt sich
E
. Die "Bandlücke" bestimmt die kritische Temperaschreiben als D(E ) = D0
E 2 − Δ2
Δ(0 K )
= 1,764 . [Bild 8]
tur des Supraleiters, es gilt näherungsweise:
k TC
Die "Bandlücke" sinkt mit steigender Temperatur, da die Wahrscheinlichkeit steigt,
dass Cooperpaare aufbrechen, und schließlich wird Δ(TC ) = 0 . Daraus ergibt sich
auch die oben diskutierte Temperaturabhängigkeit von HC und jC. [Bild 9]
Durch die Kopplung an Phononen ist die "Bandlücke" Δ (und damit auch die Sprungtemperatur TC) abhängig von der Atommasse, zeigt also einen Isotopeneffekt. Man
findet Δ ~ M–1/2 (und TC ~ M–1/2) entsprechend der Betrachtungen über Phononen (es
war ja ωmax =
α
M
). [Bild 10]
3. Supraleiter II. Art
In einigen Materialien mit hohen Sprungtemperaturen liegt zwischen dem supraleitenden und dem normalleitenden Zustand ein Zwischenzustand (Shubnikov-Phase)
vor, bei dem einige Gebiete im Supraleiter normalleitend werden, so dass lokal ein
Magnetfeld eindringen kann. Die Bereiche ordnen sich in Flußschläuchen an, die den
magnetischen Fluss tragen; Änderungen des Magnetfelds oder das Einspeisen eines
Transportstroms führen zu einer Wanderung der Flußschläuche, was mit einem
Energieaufwand verbunden ist (und durch Pinning an Defekten verhindert werden
kann). Mit steigender Temperatur nehmen diese Bereiche immer größeren Raum ein,
damit sinkt die kritische Feldstärke HC(T) und die Permittivität χ nimmt zu (–1 < χ <
0), bis schließlich bei TC2 das ganze Material normalleitend (und diamagnetisch) wird.
Solche Werkstoffe heißen Supraleiter II. Art; einige Vertreter wie z.B. NbTiLegierungen oder Nb3Sn können wesentlich höhere kritische Magnetfelder tragen als
"klassische" Magnete oder Supraleiter I. Art.
[Bild 11] [Bild 12] [Bild 13] [Bild 14]
4. Hochtemperatur-Supraleiter
Bednorz und Müller fanden 1986 erstmals Supraleiter mit Sprungtemperaturen TC
über 30 K. In verwandten Werkstoffen konnten kurz darauf TC-Werte von bis zu 130
K gemessen werden. Durch die Verfügbarkeit von Supraleitern, die mit flüssigem
Stickstoff (77 K) betrieben werden können, wurde diese Technologie für viele industrielle Anwendungen erst interessant.
Gemeinsam ist diesen "Supraleitern III. Art" eine komplexe Kristallstruktur (meist Perowskit-ähnlich) besitzen, in planare CuO-Ebenen auftreten. Erst ein Sauerstoffdefizit
(stöchiometrische Abweichung) führt zur Ausbildung einer supraleitenden Phase.
Auch heute noch ist der Mechanismus der Supraleitung in diesen Materialien nicht
vollständig verstanden. Durch die komplexe Kristallstruktur kann der Supraleiter wohl
als "Mischsystem" von normalleitenden/isolierenden und supraleitenden Schichten
aufgefasst werden, meist ist deshalb auch keine exakte "Bandlücke" Δ bestimmbar.
Der am meisten untersuchte Hochtemperatur-Supraleiter ist YBCO (YBa2Cu3O7–y,
sog. 1-2-3-Supraleiter) mit TC = 90 K. Die Werkstoffe sind sehr spröde und werden
mit keramischen Verfahren (Sintern) hergestellt. Die Einstellung der Stöchiometrieabweichung ist technologisch sehr aufwändig. Mittlerweile ist es aber gelungen,
meterlang Drähte aus Hochtemperatur-Supraleitern zu ziehen. [Bild 15] [Bild 16]
5. Bilder
Bild 1: Periodensystem der
Elemente mit Supraleitern
(grau). Die Sprungtemperatur ist jeweils in K eingetragen. Dunker schraffierte
Elemente werden nur in einer Hochdruckmodifikation
supraleitend
Bild 2: Temperaturabhängiger Widerstand von Quecksilber (Originalmessung von Onnes 1911)
Bild 3: Spezifische Wärme von normal- und
supraleitendem Al; bei T < TC wurde die
normalleitende Phase durch Anlegen eines
Magnetfelds H > HC erzwungen
Bild 4: Meissner-Ochsenfeld-Effekt: Der
Der Supraleiter verdrängt das Magnetfeld
Bild 5: Abhängigkeit der kritischen
Feldstärke HC von der Temperatur T
Bild 6: London-Eindringtiefe
und Abschwächung des inneren Magnetfelds in ein
Volumenmaterial (links) und
in einer dünnen Schicht
(rechts). Typische Werte für
ΛL sind 25 nm.
Bild 7: Das Elektron „zieht“ eine Gitterdeformation hinter sich her. Diese Gitterdeformation zieht ein zweites Elektron an (Austausch „virtueller Phononen“)
Bild 8: Energielücke Δ zwischen
dem BCS-Grundzustand und den
Zuständen angeregter Elektronen
(links); die Zustandsdichte in der
Nähe minimaler Einteilchenenergien geht gegen unendlich
(rechts)
Bild 9: Temperaturabhängigkeit der „Bandlücke“ Δ.
Bild 10: Isotopeneffekt für Zinn.
Bild 11: Verhalten von Supraleitern 1. und 2. Art. Zwischen BC1 und BC2 bildet sich
die Shubnikov-Mischphase aus
Bild 12: Shubnikov-Mischphase mit Flußschläuchen, durch die das Magnetfeld tritt
und die durch Ringströme begrenzt werden
Bild 13: BC, BC1 und BC2 einer IndiumWismut-Verbindung in Abhängigkeit
von der Temperatur
Bild 14: Flußschläuche an einer polykristallinen Oberfläche. Die Flußschläuche
werden an Korngrenzen „gepinnt“.
Bild 15: Perowskit-Struktur A2BO4. Für
B = Cu (z.B. in Ba2CuO4) sieht man
die CuO-Ebenen bei z = 0 und z = ½.
Bild 16: Temperaturabhängigkeit des Widerstands (links) und der Suszeptibilität
(rechts) eines Hochtemperatur-Supraleiters. Man sieht den graduellen Übergang von
χ analog zu einem Supraleiter 2. Art.