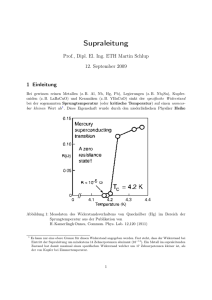
Supraleitung - Freie Universität Berlin

Supraleitung (B4)
Christopher Bronner, Frank Essenberger (GB4)
Freie Universität Berlin
Tutor: Dr. Denner
11. September 2007
Versuchsdurchführung am 10. September 2007
1
1.1
Vorbereitung
Allgemeines
Die Supraleitung wurde bei der Untersuchung des Widerstandes von Quecksilber bei geringen Temperaturen (≈ 4 K) im Jahre 1911 entdeckt. Dabei bemerkte man, dass ab einer Sprungtemperatur Tc das
Material keinen messbaren Widerstand mehr hatte. Langzeitmessungen (über zwei Jahre) zeigten, dass
der Widerstand um mindestens den Faktor 1010 kleiner seinen musste als bei normalen Leitern. Mit
Hilfe der BCS-Theorie konnte dann gezeigt werden, dass es sich wirklich um widerstandsfreie Ströme
handelt.
Desweiteren tritt ein kritisches Magnetfeld Bc auf. Sobald ein Supraleiter vom Typ 1 einem magnetischen Feld größer als Bc ausgesetzt wird verliert er seine Supraleitfähigkeit. Die Existenz eines
solchen kritschen Magnetfeldes zieht die Existenz eines kritischen Stroms Ic nach sich, da jeder Strom
ja ein magnetisches Feld erzeugt, welches den selben Effekt hat wie ein äußeres Feld.
Abbildung 1: Links: Bereiche in denen Supraleitung und normale Leitfähigkeit auftreten und Rechts:
Daten für einige Metalle [2]
An der Abb. 1 sieht man, dass das kritische Feld Bc eine Funktion der Temperatur ist. Für viele
Supraleiter lässt sich dieser Zusammenhang durch:
2 !
T
Bc (T ) = Bc (0) · 1 −
(1)
Tc
1
parametrisieren. Zur Berechnung der kritischen Feldstärke am absoluten Nullpunkt kann folgende
Formel verwendet werden.
r
µ0 γρ
Bc0 = Tc
(2)
2M
Darin ist M das Molgewicht, ρ die Massendichte und γ die Sommerfeldkonstante. Wenn die Sprungtemperatur höher als der Siedepunkt von Stickstoff (77, 35 K) ist, spricht man von Hochtemperatursupraleitung. Der momentane Rekordhalter ist Hg0,8 T l0,2 Ba2 Ca2 Cu3 O8 mit einer Sprungtemperatur
von 138 K. Für Supraleiter von Typ 2 gibt es zwei kritische magnetische Felder (Bc1 und Bc2 ) . Sobald
die erste Schwelle Bc1 erreicht ist bilden sich Kanäle aus, in denen das Feld durch den Supraleiter
fleißen kann. Diese Kanäle nehmen in Anzahl und Durchmesser mit steigendem Feld zu, bis die zweite
Schwelle Bc2 erreicht ist und der Supraleiter normal leitend wird.
Abbildung 2: Links: Magnetisierungskurve, wobei −4πM := H − B, also B = 0 für die Ursprungsgerade ist und mit wachsendem B-Feld im inneren gegen Null geht. Rechts: Messung der Feldkanäle an
P b0,98 In0,02 .
1.2
Der Normalleiter
Der klassische Normalleiter, typischerweise ein Metall, besteht aus einem Gitter1 aus Atomrümpfen
(d.h. die elementaren Atome mit den gefüllten Elektronenschalen) und einem Elektronengas. Dieses
Elektronengas meint die von den Rümpfen abgetrennten Valenzelektronen, die im quantenmechanischen Bild über den gesamten Festkörper delokalisiert sind. Vereinfachend betrachtet man meist nur
das sog. „freie Elektronengas“, in dem keine Wechselwirkung der Valenzelektronen mit der Gitterstruktur des Kristalls betrachtet wird. In diesem einfachen Fall entspricht die Energie eines Elektrons gerade
der kinetischen Energie, also ist
E
=
1
p~2
p2x + p2y + p2z =
.
2me
2me
(3)
Die Zustandsdichte N (E) des Elektronengases, also die Zahl der besetzten Zustände in einem bestimmten Energieintervall Z(E) dividiert durch eben dieses Intervall, ist allgemein als
N (E)
=
dZ(E)
dE
definiert. Im Impulsraum beschreiben die besetzten Zustände eine Kugel. Daher ist die Zahl der besetzten Zustände eines Energieintervalls propotional zum Volumen einer Kugelschale im Impulsraum.
Z(p) ∝
1 Das
p2 |d~
p|
Gitter wird zunächst als ruhend angenommen, was dem Fall T = 0 entspricht.
2
Unter Verwendung von Gl. (3) erhält man damit
Z(E) ∝
√
EdE
und also
N (E) ∝
√
E.
Da Elektronen Fermionen sind, kann jeder Zustand nur von einem Elektron bevölkert werden. Daher
werden Zustände bis zur Fermi-Energie EF besetzt. Bei endlichen Temperaturen erhält man jedoch
eine „Aufweichung“ dieser Fermi-Kante, die durch die Fermi-Funktion
F
1
=
e
E−EF
kB T
+1
beschrieben wird. Diese Funktion multipliziert mit N ergibt die Zustandsdichte bei Temperaturen
ungleich Null.
1.3
Supraleitung
Als Supraleitung bezeichnet man die Eigenschaft vieler Metalle, bei sehr geringen Temperaturen
i.d.G.v. 1 K ihren elektrischen Widerstand zu verlieren2 . Die theoretische Beschreibung dieses Phänomens liefert die Theorie von Bardeen, Cooper und Schrieffler (BCS-Theorie, 1957).
In dieser Theorie werden sog. Cooper-Paare aus zwei Elektronen eingeführt, die über virtuelle
Phononen eine attraktive Wechselwirkung aufeinander ausüben. Aus energetischen Gründen haben
diese Elektronen unterschiedliche Spins und also ist das Cooper-Paar als Boson anzusehen. In Frage
kommen für die Bildung von Cooper-Paaren nur die schnellen, delokalisierten Valenzelektronen, da
nur sie eine hinreichende Wechselwirkungsreichweite erreichen können, sodass die Coulomb-Abstoßung
übertroffen wird.
Eine frühe Bestätigung dieser Theorie fand man damals im Isotopeneffekt, der von der BCS-Theorie
vorhergesagt wird.
√ Dabei ist die Schwingungsfrequenz der Gitteratome im Kristall abhängig von ihrer
Masse (ω ∝ 1/ m), wodurch man unterschiedliche kritische Temperaturen erhält. Dieser Effekt konnte
bald experimentell bestätigt werden.
Da die Cooper-Paare Bosonen sind, unterliegen sie nicht der Fermi-Statistik und wenn man Prozesse
betrachtet, bei denen ein Cooper-Paar in zwei Elektronen (Fermionen) aufgebrochen wird, sind beide
Statistiken unzureichend.
Die Theorie fordert3 eine Ununterscheidbarkeit der Cooper-Paare, was z.B. eine Anregung eines
einzelnen Paares verbietet. Möglich ist allerdings eine Trennung des Paares in zwei Elektronen. Die
dazu nötige Energie ist gerade die Bindungsenergie des Cooper-Paares und ergibt sich aus der Theorie
als Bandlücke i.d.G.v. kleinen Temperaturen direkt an der Fermi-Kante.
Die Temperatur, bei der (ohne angelegtes Magnetfeld) Supraleitung eintritt, nennt man die Sprungtemperatur. Sie wird mit Tc bezeichnet. Für Elemente liegt sie im Bereich von wenigen Kelvin, für
unsere beiden Proben bei 3,407 K (In) und 3,722 K (Sn) [2].
1.4
Meißner-Ochsenfeld-Effekt
Der Meißner-Ochsenfeld-Effekt ist eine charakteristische Eigenschaft von Supraleitern. Dieser Effekt
besagt, dass der Supraleiter in seinem Inneren feldfrei ist, also äußere magnetische Felder verdrängt.
Dabei spielt es keine Rolle, ob der Supraleiter erst supraleitend und dann das Feld hinzu kommt, oder
anders herum. In der Reihenfolge zuerst T < Tc einzustellen und dann Feld einschalten ist dieser
Effekt klar. Auf Grund des sich ändernden Magnetfeldes entstehen Kreisströme, welche der Ursache
(dem äußeren Magnetfeld) entgegen gerichtet sind. Da kein Widerstand vorhanden ist werden diese
Ströme so groß, dass sie die äußeren Felder genau abschirmen (d.h. χ = −1).
2 Natürlich kann experimentell nur ein Abfallen unter die Grenze der Messbarkeit festgestellt werden, nicht aber ein
absolutes Verschwinden.
3 Aufgrund der experimentellen Ergebnisse. [1], Abschn. 2.2, S. 37.
3
Aber auch in der Reihenfolge erst das Feld einzuschalten und danach T < Tc einzustellen wird das
Feld auf dem Supraleiter verdrängt - entgegen jeder klassischen Vorstellung.
Abbildung 3: Feldverdrängung beim Übergang zum supraleitenden Zustand
Hierbei wird klar, dass ein Supraleiter mehr ist als ein perfekter (meint widerstandsfreier) Leiter.
1.5
Thermodynamik und thermische Eigenschaften des supraleitenden Zustandes
Um zu beurteilen, ob eine Phase gegen eine andere stabil ist, kann man die Gibbs-Funktion der Variablen T und p heranziehen. Diese als freie Enthalpie bekannte Funktion ist definiert als
G = U − T S + pV
und
dG = dU − dT S − dST + dpV + dV p.
Mit der Definition der Gibbs-Funktion der Entropie S und des Volumens V auch als innere Energie
bekannt ergibt sich:
dU
= T dS − pdV
⇒ dG = −SdT + V dp.
(4)
Diese Funktion ist experimentell sehr angenehm, da man die Temperatur und den Druck eines Systems
leicht von außen beeinflussen kann. Die Reversibilität (s. Der Meißner-Ochsenfeld-Effekt) ist ein Beleg
für die Existenz einer supraleitenden Phase. Nun betrachten wir die Enthalpien der supraleitenden
Phase Gs und der normal leitenden Phase Gn . Hier muss noch ein Term für das magnetische Feld
eingeführt werden:
~ .
dG = −SdT + V dp − d m
~ ·B
~ ist und dB = 0 ist ergibt sich:
Da das magnetische Moment mk
~ B
dG = −SdT + V dp − dmB.
Es gilt
4
(5)
• Gs < Gn für T < Tc . Die supraleitende Phase ist also stabil.
• Gs = Gn für T < Tc . Hier findet ein Phasenübergang statt.
• Gs > Gn für T > Tc . Die normale Phase ist also stabil.
Aus Gl. (5) mit dp = dT = 0 und der Tatsache, dass Gs (Bc ) − Gn (Bc ) = 0 folgt die Gleichung
Bc
Z
Gs (Bc , T ) − Gs (0, T ) = −
mdB.
0
Nun noch ausnutzen, dass sich Gs (Bc , T ) = Gn (Bc , T ) = Gn (0, T ) umschreiben lässt. Gn soll ja nicht
von Feldern abhängen.
Z Bc
Gn (Bc , T ) − Gs (0, T ) = −
mdB.
0
Jetzt muss nurnoch ein Zusammenhang für m = m(B) angenommen werden. Wir wählen den einfachsten, nämlich einen linearen. m =
M
· |{z}
V
= χ µB0 · V . Mit der Suszeptibilität von −1 für
|{z}
Magnetisierung Volumen
die supraleitende Phase ergibt sich so:
Gn (T ) − Gs (T ) =
Vs
µ0
Z
Bc
BdB =
0
Vs 2
B .
2µ0 c
Wenn man nun den Zusammenhang, dass Bc = Bc (T ) berücksichtigt und dass
∂S
T ∂T
= cp ist ergibt sich:
p,B
Sn (T ) − Ss (T )
cn (T ) − cs (T )
∂G
∂T |B,p
= −S und
Vs
∂Bc
.
· Bc ·
µ0
∂T
=
−
=
∂
Vs T
T
(Sn (T ) − Ss (T )) = −
∂T
µ0
∂Bc
∂T
2
∂ 2 Bc
+ Bc ·
∂T 2
!
Nun kann man noch Gl. (1) verwenden und erhält dann
2 ! Vs
T
2T
2
Sn (T ) − Ss (T ) = −
· Bc (0) · 1 −
· − 2
µ0
Tc
Tc
cn (T ) − cs (T )
=
=
2 ! !
∂
T Vs Bc (0)2 ∂
T
2T
T
(Sn (T ) − Ss (T )) = −
·
1−
· − 2
∂T
µ0
∂T
Tc
Tc
T 3
2T Vs Bc (0)2
3T 2
2T Vs Bc (0)2 ∂
·
T
−
=
·
1
−
µ0 Tc2
∂T
Tc2
µ0 Tc2
Tc2
Im Fall T = Tc erhält man also
cn (T ) − cs (T )
2
= −
4Vs Bc (0)2
.
µ0 T
Aufgaben
1. Bestimmen der Sprungtemperaturen für Indium und Zinn. Welches sind die Ursachen für eine
endliche Übergangsbreite?
2. Bestimmung von Bc (T ) für beide Metalle anhand von Messungen bei unterschiedlichen Temperaturen. Extrapolieren von Bc0 .
3. Berechnung von Bc0 und Vergleich mit den gemessenen Werten.
5
4. Skizze des Versuchsaufbaus.
5. Weshalb misst man die Änderung der Suszeptibilität und nicht den Widerstand, i.e. warum kann
die Widerstandmethode falsche Ergebnisse liefern?
6. Herleitung von ∆c aus ∆S und Diskussion von ∆c an der Stelle T = Tc .
7. Weshalb kann man die Spannung mit dem Kompensationprinzip genauer messen?
3
3.1
Messprotokoll
Versuchsaufbau
Abbildung 4: Versuchsaufbau
Kern des Aufbaus waren zwei ineinandergesteckte Kryostaten. Im inneren war flüssiges Helium eingefüllt, das von einer Vakuumschicht umgeben im äußeren Kryostaten, der mit flüssigem Stickstoff gefüllt
war, eingelassen war. Die Wände der Kryostaten waren mit einer Silberschicht verspiegelt um die Wärmestrahlung von außen zu reflektieren. Das Vakuum der Trennwand wurde durch eine Drehschieberund eine Öldiffusionspumpe erzeugt und betrug etwa 10−5 mbar. In der zentralen Kammer waren die
Proben an einem langen Stab angebracht und von jeweils zwei Spulen umgeben, die den Transformator
bildeten. Daneben war eine Spule ohne Medium zum Vergleich angebracht.
6
Abbildung 5: Transformatorspulen mit Proben
Der innerste Kryostat konnte mit einer weiteren Drehschieberpumpe auf die nötigen Drücke gepumpt werden. Auf diese Weise ließ sich die Temperatur in der Apparatur regeln. Der untere Teil der
Kryostaten mit den Proben war von einer Feldspule umgeben, die von einem Netzgerät mit maximal 6
A betrieben wurde. Die Signale von den Proben konnten mittels eines Lock-In-Verstärkers verarbeitet
(Integration) und auf Oszilloskop oder Multimeter analysiert werden.
Der Lock-In-Verstärker bildet zunächst das Differenzsignal von Referenz- und Probenspule, welches
wieder einen Sinus bildet. Über dieses Signal legt er dann ein Rechtecksignal, um phasensensitiv eine
Integration durchführen zu können, sodass man auf einem Multimeter die mittlere Spannung des
Differenzsignals ablesen kann.
Abbildung 6: Schematische Skizze des Aufbaus
7
3.2
Vorbereitungen
Bevor wir mit den eigentlichen Messreihen beginnen konnten, mussten wir das Vakuum in der Zwischenwand der Kryostaten erzeugen, mit dem Manometer die Dichtheit der Apparatur überprüfen, das
Wasser im äußeren Kryostaten entfernen. Anschließend konnten wir zunächst den Stickstoff und nach
einer Wartezeit auch das Helium einfüllen.
3.3
Bestimmung der Sprungtemperaturen
Um die Sprungtemperaturen zu messen, pumpten wir mit der Drehschieberpumpe und ließen die Luft
mit Hilfe eines Nadelventils langsam entweichen. Der stetige Druckverlust entsprach einer Temperaturabsenkung, die einerseits grob am Manometer abzulesen war, andererseits (genauer) über einer
Umrechnungstabelle bestimmt werden kann.
Während der Druck abfiel, maßen wir die Spannung am Lock-In-Verstärker, die proportional zur
Suszeptibilität war. Vor den Messreihen, in der „Plateau-Phasse“ passten wir die Phase am Lock-InVerstärker so an, dass ∆U = 0 war. So messen wir immer die negative Differenz zum Plateau.
p / mbar
638
634
630
626
624
622
620
618
616
614
612
610
608
606
604
602
600
598
596
591
592
590
588
586
582
574
∆U / mV
-5
-5
-6
-8
-8
-11
-14
-16
-23
-28
-42
-65
-84
-129
-221
-348
-444
-553
-586
-615
-627
-633
-639
-641
-647
-652
p / mbar
450
440
436
432
428
426
424
422
422
420
418
417
416
415
414
413
412
411
410
409
408
407
406
405
404
402
400
398
396
388
∆(∆U ) / mbar
1
1
1
1
1
1
1
1
1
1
2
2
2
3
6
7
6
6
3
2
2
1
1
1
1
1
∆U / mV
0
0
0
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-2
-6
200
417
712
945
∆(∆U ) / mbar
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
23
24
32
25
1071
1091
1098
12
4
3
1106
1108
1111
1112
1113
1115
2
2
2
2
2
2
Tabelle 1: Bestimmung von Tc bei Sn (links) und In (rechts). Für den Druck gilt durchweg ein Gerätefehler von 2 mbar. Der Ablesefehler ist dagegen klein.
8
3.4
Bestimmung der kritischen Magnetfeldstärken
Um die Feldstärke zu bestimmen, bei der die Supraleitung zusammenbricht, haben wir bei konstantem
Druck (243 mbar, 100 mbar, 50 mbar und 30 mbar), also konstanter Temperatur, den Spulenstrom von
Null auf sechs Ampère erhöht um zu sehen, wann die Differenzspannung Null wird. Um die Nulllage
festzulegen, haben wir vorher jeweils eine Nullmessung bei maximaler Stromstärke durchgeführt.
Es ist noch zu bemerken, dass die Drücke während der einzelnen Messungen zwar die allermeiste Zeit
nicht sichtbar schwankten, aber dennoch das eine oder andere Mal um maximal 4 mbar abwichen, was
wir dann sofort korrigierten. Die Schwankungen bleiben in der weiteren Auswertung unberücksichtigt.
I /A
5,94
0,00
0,60
0,70
0,80
0,89
1,02
1,10
1,23
1,30
1,40
1,50
1,80
2,10
2,54
3,00
4,00
6,00
∆I / A
0,04
0,01
0,01
0,01
0,01
0,01
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,03
0,03
0,04
I /A
5,97
0,00
0,50
0,60
0,70
0,80
0,90
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
2,00
2,10
2,20
2,30
2,40
2,49
2,59
3,00
4,00
6,00
∆U / mV
0
-1010
-1002
-984
-939
-835
-609
-456
-245
37
37
36
31
24
8
7
5
0
∆I / A
0,04
0,01
0,01
0,01
0,01
0,01
0,01
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,03
0,03
0,04
∆U / mV
-1
-577
-574
-573
-571
-569
-569
-580
-581
-593
-580
-561
-545
-520
-488
-450
-402
-332
-216
-79
-7
-7
-7
-6
-4
-1
Tabelle 2: Messung von Bc (T ) bei p = 243 mbar an In (links) und Sn (rechts). Für ∆U gilt jeweils ein
Fehler von 1 mV.
9
I /A
5,95
0,60
0,78
0,99
1,21
1,40
1,60
1,70
1,80
1,90
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,79
2,9
3,1
3,69
3,95
8,09
5,98
∆I / A
0,04
0,01
0,01
0,01
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,03
0,03
0,03
0,05
0,04
∆U / mV
0
-1006
-1005
-1002
-997
-987
-964
-938
-910
-864
-806
-729
-616
-517
-408
-286
-309
-87
29
28
25
13
4
2
0
I /A
6,00
0,00
1,00
1,42
1,83
2,21
2,41
2,59
2,80
3,00
3,20
3,35
3,41
3,53
3,62
3,70
3,80
4,09
4,51
3,92
4,00
5,03
5,99
∆I / A
0,04
0,01
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,04
0,04
∆U / mV
0
-572
-566
-553
-537
-537
-533
-514
-508
-465
-409
-356
-330
-263
-212
-151
2
-3
-2
-3
-3
-1
0
Tabelle 3: Messung von Bc (T ) bei p = 100 mbar an In (links) und Sn (rechts). Für ∆U gilt jeweils ein
Fehler von 1 mV.
10
I /A
6,00
0,60
0,80
1,20
1,60
2,00
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
4,00
4,20
4,40
4,65
5,00
6,00
∆I / A
0,04
0,01
0,01
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,04
0,04
∆U / mV
0
-1000
-1000
-998
-992
-973
-906
-872
-815
-766
-695
-599
-502
-415
-313
-210
-270
-14
24
23
22
20
17
13
3
2
0
I /A
6,00
0,00
1,00
1,48
2,03
2,39
2,70
3,01
3,30
3,50
3,70
3,90
4,00
4,10
4,20
4,30
4,40
4,50
4,60
4,70
4,80
4,90
5,00
5,50
6,00
∆I / A
0,04
0,01
0,02
0,02
0,02
0,02
0,02
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,04
0,04
0,04
∆U / mV
0
-572
-568
-561
-545
-533
-524
-517
-500
-484
-445
-386
-352
-307
-246
-191
-195
-217
-156
-5
-3
-4
-4
-2
-1
Tabelle 4: Messung von Bc (T ) bei p = 50 mbar an In (links) und Sn (rechts). Für ∆U gilt jeweils ein
Fehler von 1 mV.
11
I /A
6,10
0,01
1,00
2,00
2,50
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
4,00
4,20
4,00
4,60
5,00
5,50
∆I / A
0,04
0,01
0,02
0,02
0,02
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,04
0,04
∆U / mV
0
-992
-992
-980
-934
-775
-718
-640
-574
-483
-387
-354
-212
-295
-265
24
21
18
15
5
0
I /A
6,10
0,00
1,00
2,00
3,00
3,50
4,00
4,20
4,40
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,50
5,70
6,00
∆I / A
0,04
0,01
0,02
0,02
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,03
0,04
0,04
0,04
0,04
0,04
0,04
0,04
∆U / mV
0
-569
-566
-548
-519
-507
-471
-423
-371
-303
-235
-200
-185
-7
-5
-5
-4
-3
-2
-2
Tabelle 5: Messung von Bc (T ) bei p = 30 mbar an In (links) und Sn (rechts). Für ∆U gilt jeweils ein
Fehler von 1 mV.
4
4.1
Auswertung
Sprungtemperatur
Um die Übergangstemperatur Tc der beiden Metalle zu bestimmen, tragen wir die gemessenen Spannungsdifferenzen ∆U gegen die gemessenen Drücke auf. So erhalten wir einen Druck, in dessen Umgebung die gemessenen Spannung, die zur Suszeptibilität χ des Materials proportional ist, schnell
umschlägt. Den Wert für diesen Druck können wir mit Hilfe der Umrechnungstabelle in eine Temperatur übersetzen.
12
Abbildung 7: Bestimmung von Tc an Sn
Abbildung 8: Bestimmung von Tc an In
In den Abbn. 7,8 sind die entsprechenden Messwerte aufgetragen. Der Umschlagpunkt wurde durch
manuelles Fitten einer Ausgleichsgerade durch den linearen teil der Werte und deren Schnittpunkt mit
13
einer Geraden für χ = χmax /2 bestimmt. So erhalten wir die Drücke an den Umschlagpunkten,
pc,Sn
=
(602 ± 2) mbar
pc,In
=
(412 ± 2) mbar,
und also lauten die Sprungtemperaturen
Tc,Sn
=
(3, 706 ± 0, 003) K
Tc,In
=
(3, 386 ± 0, 004) K.
Die endliche Übergangsbreite in den obigen Kurven resultiert zum einen aus der Ungleichmäßigen Temperaturausbreitung im Kryostaten und in der Probe. Während des konstanten Druck- und
damit Temperaturabfalls (am Manometer abgelesen) kühlte die Probe wahrscheinlich nicht an allen
Stellen gleichmäßig ab, sodass einige Bereiche schon supraleitend waren, andere noch nicht. Desweiteren war das Magnetfeld innerhalb der Transformatorspule sicherlich nicht perfekt homogen und diese
Inhomogenitäten haben sich vermutlich zwischen den beiden Spulen, deren Signale in die Differenzmessung eingegangen sind, auch noch unterschieden. Desweiteren können aufgrund von Unreinheiten
des Probenmaterials auch einige andersartige Cooper-Paare vorhanden sein, die bei anderen Energien
entstehen.
4.2
4.2.1
Kritische Magnetfeldstärken
Bestimmung von Bc (T ) an den vier Messpunkten
Um die kritische Magnetfeldstärke Bc (T ) für die vier Temperaturen zu bestimmen, tragen wir analog
zu oben die Spannung ∆U über dem Spulenstrom I auf, woraus wir wieder einen Umschlagstrom Ic
erhalten werden, den wir mit Hilfe der gegebenen Formel
B/G
=
(45 ± 1) · I/A
umrechnen können.
Abbildung 9: Messung bei p = 243 mbar. Links Sn, rechts In.
14
Abbildung 10: Messung bei p = 100 mbar. Links Sn, rechts In.
Abbildung 11: Messung bei p = 50 mbar. Links Sn, rechts In.
15
Abbildung 12: Messung bei p = 30 mbar. Links Sn, rechts In.
Die Werte, die wir aus den Graphen abgelesen haben, sind in Tabelle 6 dargestellt. Als fünften Wert
verwenden wir jeweils die gemessene Sprungtemperatur bei abgeschaltetem Spulenstrom (Abschn. 4.1).
p / mbar
243 ± 2
100 ± 2
50 ± 2
30 ± 2
T /K
3,01±0,02
2,48±0,05
2,2±0,1
2,0±0,2
(Tc )
Sn: Ic / A
2,1±0,1
3,5±0,1
4,2±0,1
4,7±0,1
0
Sn: Bc / G
92±4
157±6
187±5
209±6
0
In: Ic / A
1,1±0,1
2,3±0,1
3,0±0,1
3,4±0,1
0
In: Bc / G
48±3
103±5
135±5
153±6
0
Tabelle 6: Übersicht der gemessenen Werte
4.2.2
Verifizieren der parabolischen Form und Extrapolation auf Bc0
Wir wollen nun die theoretische Beziehung Gl. (1),
Bc (T )
=
Bc (0) ·
1−
T
Tc
2 !
,
überprüfen und tragen dazu Bc über T 2 /Tc2 (linearisiert) auf (vgl. Abb. 13). Wie man in der Grafik
erkennt, bestätigen unsere Messungen den obigen Zusammenhang.
16
Abbildung 13: Linearisierte Auftragung für Sn (links) und In (rechts)
Die Extrapolation4 auf T = 0 ergibt die thermodynamisch kritischen Felder Bc0 :
Bc0,Sn
=
(285 ± 5) G
Bc0,In
=
(228 ± 3) G
Wir können diese Feldstärken durch Gl. (2) überprüfen; die notwendigen Zahlenwerte entnehmen wir
dem Praktikumsskript. Für die kritische Temperatur benutzen wir den Literaturwert.
4.3
4.3.1
T heo
Bc0,Sn
=
308, 6 G
T heo
Bc0,In
=
280, 0 G
Zusätzliche Fragen
Widerstandsmethode
Bei dieser Methode besteht die Gefahr, dass sich schon vor Eintritt der vollständigen Supraleitung
kleine supraleitende Bereiche (etwa durch Verunreinigungen) ergeben könnten, die dann ebenfalls schon
für einen Widerstand von Null sorgen würden.
4.3.2
Differenz der spezifischen Wärmen
Die Herleitung findet sich am Ende von Abschn. 1.5.
4.3.3
Kompensationsprinzip
Durch die Differenzmessung eliminieren sich Fehler, die aus der Inhomogenität der Felder in den
Transformatorspulen resultieren. Allerdings ist das nur dann der Fall, wenn die Bauweise der jeweiligen
Spulen hinreichend ähnlich ist.
5
Diskussion
Allgemein ist der Versuch als erfolgreich zu bewerten, da die zu beobachtenden Effekte allesamt der
Erwartung entsprachen. Die Sprungtemperaturen ließen sich relativ genau messen (wenn auch ein
kleiner systematischer Fehler enthalten ist), die kritischen Magnetfeldstärken weisen allerdings eine
große Abweichung auf, die wir nicht näher erklären können.
Diese Ergebnisse spiegeln sich schon in den Graphen wider: die Plots für die Temperaturmessung
sind viel „schöner“ als die für die Magnetfeldmessung, in denen die Kurve oft über oder unter den
Maximal- bzw. Minimalwert hinausgeht oder in denen dem eigentlichen Anstieg ein kleinerer vorrausgeht.
4 Ausgabe
von Origin beim Fitten der Ausgleichsgeraden.
17
5.1
Sprungtemperaturen
Tc,Sn
=
(3, 706 ± 0, 003) K
Tc,In
=
(3, 386 ± 0, 004) K
Lit
Tc,Sn
Lit
Tc,In
=
3, 722 K
=
3, 407 K
Die Tatsache, dass die gemessenen Temperaturen beide Male zu klein sind, resultiert vermutlich
daraus, dass der Druck nicht für jede Messung auf einem konstanten Wert gehalten wurde, bis die gesamte Probe die entsprechende Temperatur erreicht hatte. Der gemessene Dampfdruck gibt schließlich
nur die aktuelle Temperatur des Helium-Gases über der Flüssigkeit, in der die Proben liegen, wieder.
Bis die Probe selbst auch diese Temperatur angenommen hat, ist das Gas bereits weiter abgekühlt
(wir senkten den Druck ja kontinuierlich).
Dennoch liegen die gemessenen Werte recht nah bei den Literaturwerten, sodass wir schließen
können, keine gröberen Fehler bei der Messung gemacht zu haben.
5.2
Kritische Feldstärken
Der parabolische Zusammenhang zwischen kritischer Feldstärke und der Temperatur konnte sehr gut
nachgewiesen werden. Leider sind die Werte der thermodynamisch kritischen Felder signifikant von
Literaturwerten und berechneten Werten verschieden, wie in Tabelle 7 erkennbar. Wegen des erwartungsgemäßen Verlaufs der Messwerte vermuten wir einen systematischen Fehler als Ursache für die
große Abweichung.
Probe
Sn
In
Gemessen
285 ± 5
228 ± 3
Berechnet mit Gl. (2)
308, 6
280, 0
Literatur [3]
305±2
282±2
Tabelle 7: Vergleich der Werte für Bc0 in Gauß
Wie man an Abb. (3) sieht wird das Magnetische Feld an der Oberfläche des Supraleiters verformt.
Dies für zu einer Verstärlung des Feldes und könnte die Abweichung erklären.
Literatur
[1] W. Buckel: Supraleitung. VCH, Weinheim 1990.
[2] E. A. Lynton: Superconductivity. Wiley & Sons, New York 1964.
[3] CRC - Handbook of Chemistry and Physics
18