Supraleitung

Supraleitung
Prof., Dipl. El. Ing. ETH Martin Schlup
12. September 2009
1 Einleitung
Bei gewissen reinen Metallen (z. B. Al, Nb, Hg, Pb), Legierungen (z. B. Nb3 Sn), Kupferoxiden (z. B. LaBaCuO) und Keramiken (z. B. YBaCuO) sinkt der spezifische Widerstand
bei der sogenannten Sprungtemperatur (oder kritische Temperatur) auf einen unmessbar kleinen Wert ab1 . Diese Eigenschaft wurde durch den niederlädischen Physiker Heike
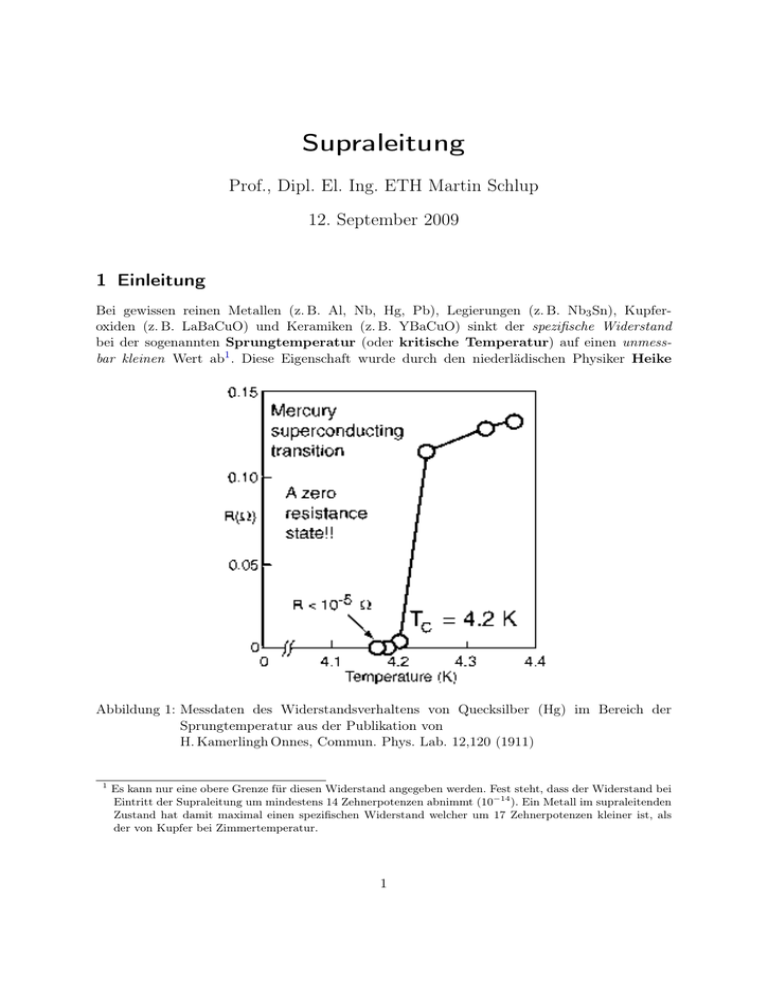
Abbildung 1: Messdaten des Widerstandsverhaltens von Quecksilber (Hg) im Bereich der
Sprungtemperatur aus der Publikation von
H. Kamerlingh Onnes, Commun. Phys. Lab. 12,120 (1911)
1
Es kann nur eine obere Grenze für diesen Widerstand angegeben werden. Fest steht, dass der Widerstand bei
Eintritt der Supraleitung um mindestens 14 Zehnerpotenzen abnimmt (10−14 ). Ein Metall im supraleitenden
Zustand hat damit maximal einen spezifischen Widerstand welcher um 17 Zehnerpotenzen kleiner ist, als
der von Kupfer bei Zimmertemperatur.
1
2 Eigenschaften
Kamerlingh Onnes (1853 - 1926) 1911 bei Quecksilber (Hg) entdeckt (cf. Abbildung 1).
H. Kamerlingh Onnes nannte das Phänomen Supraleitung (superconductivity). Die Sprungtemperatur ist bei reinen Metallen in der Regel nur wenig oberhalb des absoluten Temperaturnullpunktes (0 K ≡ -273.15 ◦ C). Entgegen allen theoretischen Voraussagen2 , entdeckten im Jahr
1986 die beiden Forscher Johannes Georg Bednorz (1950 - ) und Karl Alexander Müller
(1927 - ) ein Kupferoxyd mit einer zu jener Zeit unglaublichen Sprungtemperatur von 35 K
(Nullwiderstandsbereich unterhalb 10 K) was ihnen postwendend den Physik-Nobelpreis (1987)
einbrachte. Ein technologischer Durchbruch gelang Anfang 1987 als YBa2 Cu3 O7 (YBCO) entdeckt wurde mit einer Sprungtemperatur von etwa 93 K was eine kostengünstige Kühlung mit
flüssigen Stickstoff (Siedetemperatur bei 77 K) anstelle von flüssigem Helium möglich machte.
Den Rekord für die höchste Sprungtemperatur hielt 1993 ein Quecksilber-Barium-CalciumCuprat (Andreas Schilling, ETHZ) mit einem Wert von 133.5 K, wobei der Nullwiderstand
knapp unterhalb 95 K lag. Seit dem sind weitere Ergebnisse erzielt worden. Unter anderem
wurden auch organische Stoffe, sowie Fullerene (C60 ) entdeckt, welche supraleitend bei „hohen“
Temperaturen werden können.
2 Eigenschaften
Das Phänomen der Supraleitung lässt sich nur durch quantenmechanische Betrachtungen beschreiben und verstehen3 . Das erste erfolgreiche Erklärungsmodell ist die 1957 durch John
Bardeen (1908 - 1991), Leon Neil Cooper (1930 - ) und John Robert Schrieffer (1931 - )
aufgestellte BCS-Theorie. Diese basiert auf der Tatsache, dass in gewissen Festkörpern bei
tiefen Temperaturen (wo die Unordnung bringende thermische Energie stark abgenommen hat)
gepaarte Elektronen einen tieferen Energiepegel aufweisen können als ungepaarte. Man spricht
dabei von Cooper-Paaren. Diese Paarung wird durch das periodische Atomgitter des Festkörpers ermöglicht. Die Gitterschwingungen (so genannte Phononen) werden durch die Elektronen beeinflusst: ein Elektron zieht auf Grund seiner elektrischen Ladung das Atomgitter
etwas zusammen, so dass ein zweites Elektron durch die leicht überzählige elektrische Ladung
der Atomkerne angezogen werden kann. Wenn beide Elektronen gemäss dem Pauli-Prinzip4
einen entgegengesetzten Spin5 aufweisen6 , können sie im selben Zustand verweilen und sich wie
ein einziges Teilchen mit doppelter Elementarladung (−2e) verhalten7 . Diese Teilchen haben
nun die Eigenschaft sich widerstandsfrei8 im Atomgitter bewegen zu können, was einzelne Elektronen gerade nicht können. Das Verständnis für dieses Phänomen basiert auf der Wellennatur
der Elektronen (de Broglie-Wellen9 ) und kann nicht durch ihre Partikel-Natur erklärt werden.
Die chemischen Elemente welche supraleitendes Verhalten aufweisen können, sind im Periodensystem der Abbildung 2 dargestellt. Wie man daraus entnehmen kann, werden Cu und die
Edelmetalle Pt, Ag, Au nicht supraleitend.
2
3
4
5
6
7
8
9
Eine obere Grenze der Sprungtemperatur wurde bei 30 K vermutet.
Es gib dabei Aspekte der Supraleitung, welche sich immer noch einer theoretischen Beschreibung entziehen.
Wolfgang Ernst Pauli (1900 - 1958)
Dies ist ein quantenmechanischer Zustand, den man sich als Eigendrehung des Partikels vorstellen kann.
Dabei verschwindet der Gesamtspin.
Teilchen mit ganzzahligem Spin (Cooper-Paare haben den Spin Null) werden als Bosonen {nach Satyendranath Bose (1894 - 1974)} bezeichnet. Diese weisen ganz andere Eigenschaften auf als Fermionen {nach
Enrico Fermi (1901 - 1954)}, in diesem Fall die einzelnen Elektronen mit Spin 21 .
ohne Streuung am Atomgitter
Louis-Victor Pierre Raymond de Broglie (1892 - 1987)
2
2 Eigenschaften
Abbildung 2: Periodensystem der chemischen Elemente mit Angabe der supraleitenden Stoffe
(Stand 2009). Einige der Stoffe werden nur bei hohem Druck supraleitend.
Quelle: wuphys.wustl.edu/~jss/NewPeriodicTable.pdf
Die Sprungtemperatur und damit auch das supraleitende Verhalten ist abhängig von der
Stromdichte im supraleitenden Material. Unter anderem verschwindet der supraleitende Effekt beim Erreichen einer kritischen Stromdichte oder einer kritischen (externen) magnetischen
Feldstärke. Diese Eigenschaft bildet eine obere Grenze für die Stromstärke, welche supraleitend
fliessen kann10 .
Entsprechend ihrem Verhalten werden Supraleiter in zwei Arten eingeteilt:
• Supraleiter erster Art (Typ I ) sind dadurch charakterisiert, dass sie eine von der Stromdichte unabhängige Sprungtemperatur aufweisen, bei welcher die supraleitende in die
resistive Leitung übergeht und umgekehrt. Magnetische Feldlinien können nicht in das
supraleitende Material eindringen11 . Das vollständige Verdrängen eines (externen) Magnetfelds entspricht einem idealen diamagnetischen Verhalten. Dieses Verhalten zeigen
reine Metalle wie z. B. Al, Pb oder Hg.
Quelle: http://en.wikipedia.org/wiki/Type-I_superconductor
• Bei Supraleitern der zweiten Art (Typ II ) ist die Sprungtemperatur abhängig von der
Stromdichte, wie aus der Abbildung 3 entnommen werden kann. Sie weisen einen progressiven Übergang von supraleitender zu resistiver Leitung auf, bei zunehmender Stärke
des (externen) magnetischen Felds. Dieser progressive Übergang wird als Shubnikov10
11
Dies ist auch der Grund wieso mit supraleitenden Spulen nur begrenzte magnetische Flussdichten erreicht
werden können, aber es sind immerhin 26.8 T (2007, Quelle: http://en.wikipedia.org/wiki/Superconducting_
magnet). Für höhere (konstante) Feldwerte müssen resistive (widerstandsbehaftete) und entsprechend gekühlte Spulen benutzt werden.
Genau genommen, wird das magnetische Feld an der Oberfläche des Supraleiters durch Wirbelströme in einer
äusserst dünnen Schicht exponentiell abgebaut {cf. Gleichung (4)}.
3
2 Eigenschaften
Abbildung 3: Temperaturabhängiger Widerstandsverlauf einer La-Ba-Cu-Oxid Probe (Supraleiter zweiter Art) in Funktion verschiedener Stromdichten nach K. A. Müller und
J. G. Bednorz: Possible high Tc superconductivity in the Ba-La-Cu-O system. Z.
Physik, B 64 (1): 189–193, 1986
Phase bezeichnet: Dabei wird das magnetische Feld nur teilweise verdrängt und der
Leiter bleibt dennoch supraleitend. Dieses Verhalten zeigen metallische Legierungen und
die Hochtemperatursupraleiter.
Quelle: http://en.wikipedia.org/wiki/Type-II_superconductor
Das Verhalten eines Supraleiters lässt sich nicht einfach durch einen Leiter, bei dem der
Widerstand unterhalb der Sprungtemperatur verschwindet, erklären:
Das magnetische Verhalten beim Supraleiter hängt nämlich nicht davon ab, ob die Probe zuerst unter die Sprungtemperatur abgekühlt und dann einem Magnetfeld ausgesetzt wird oder
umgekehrt, im Magnetfeld abgekühlt wird. In beiden Fällen ist der Endzustand der selbe: das
magnetische Feld dringt nicht in den Supraleiter ein. Im Gegensatz dazu, würde bei einem
Leiter, bei dem beim Abkühlen nur gerade der Widerstand verschwindet, es nicht zu einer Verdrängung des magnetischen Felds kommen, falls dieses vor dem Abkühlen vorhanden war. Das
Phänomen der Magnetfeldverdrängung, beziehungsweise das ideale diamagnetische Verhalten,
4
2 Eigenschaften
wird Meissner-Ochsenfeld-Effekt12 genannt. Nach Abschalten des (externen) Magnetfelds
bleibt auch kein Restfeld im Leiter zurück.
Das phänomenologische Verhalten der Supraleiter (erster Art) haben 1935 die Brüder London
{Fritz Wolfgang London (1900 - 1954), Heinz London (1907 - 1970)} durch zwei Gleichungen
beschrieben:
djs
dt
B = −µ0 λ2L rotjs
(1)
E = µ0 λ2L
(2)
Die Gleichung (1) besagt, dass die Suprastromdichte js bei einer nicht-verschwindenden elektrischen Feldstärke E permanent ansteigen würde. Dies entspricht der Aussage, dass ein konstanter
Strom widerstandslos, d. h. bei Feldstärke Null, fliessen kann.
Aus Gleichung (2) kann, zusammen mit den Maxwellschen Gleichungen13 der Elektrodynamik14 , die folgende Beziehung hergeleitet werden:
∆B =
1
B
λ2L
(3)
Die Beziehung (3) beschreibt den Meißner-Ochsenfeld-Effek. Die Grösse λL ist die so genannte
London-Eindringtiefe15 . Diese hängt von der Ladung q = −2e, der Masse m und der Dichte
ns der Teilchen (Cooper-Paare) ab:
r
m
λL =
µ0 q 2 n s
Ist ein äusseres Magnetfeld parallel zur Oberfläche (z-Richtung) an den Supraleiter angelegt,
so hängt der Betrag der Stärke dieses magnetischen Felds von der Eindringtiefe des Felds (xRichtung) im Supraleiter ab. Die Lösung der Gleichung (3) ergibt in diesem Fall:
Bz (x) = Bz (0) · exp (−
x
)
λL
(4)
Zum Beispiel beträgt die Eindringtiefe bei Zinn (Sn) 26 nm, was bei einer Abschwächung auf
unter 1% der Magnetfeldstärke an der Oberfläche in etwa einer Schichtdicke von 5×26 nm ≈
0.1 µm entspricht. Für Details der Herleitung und weitere numerische Werte für die Eindringtiefe
cf. z. B.: (1) Buckel, Kleiner oder http://de.wikipedia.org/wiki/London-Gleichung.
Supraleiter der zweiten Art verhalten sich bei schwächeren magnetischen Feldern wie Supraleiter der ersten Art, d. h. sie zeigen ideales diamagnetisches verhalten. Bei sehr starken Feldern
verschwindet die Supraleitung ebenfalls. Dazwischen, in der so genannten Shubnikov-Phase,
zeigen sie nur einen unvollständigen Meißner-Ochsenfeld-Effekt: es können sich Mischzustände
12
13
14
15
Walther Meißner (1882 - 1974), Robert Ochsenfeld (1901 - 1993)
cf. http://de.wikipedia.org/wiki/Meissner-Ochsenfeld-Effekt
James Clerk Maxwell (1831 - 1879)
` z
´
∂j
x
z ∂jy
x
mit der „Rotation“ des Vektors j: rotj = ∂j
− ∂zy ; ∂j
− ∂j
; ∂x − ∂j
, den Maxwellschen Gleichungen
∂y
∂z
∂x
∂y
„Ursache des Magnetfelds“: rotB = µ0 js und „Quellenf reiheit des magnetischenF elds“ :
∂B
x
z
divB = ∂B
+ ∂yy + ∂B
=0
∂x
∂z
∆ ist der Laplace-Operator: ∆f =
der Gleichung (3) anzuwenden.
∂2f
∂x2
+
∂2f
∂y 2
+
∂2f
∂z 2
. Da B ein Vektor ist, ist er auf allen drei Komponenten
5
3 Anwendungen
von supraleitenden und resistiven Bereichten bilden, so das nicht sämtliche magnetische Feldlininen aus dem supraleitenden Material verdrängt werden. Die in den Leiter eindringenden
magnetischen Feldlinien werden in quantisierte, normal leitende Flussschläuche (Feldröhren)
„gequetscht“. Das magnetische Flussquantum dieser Röhren beträgt dabei
φ0 =
h
= 2.0678 · 10−15 Vs.
2e
(5)
Der supraleitende Zustand wird allgemein über den Meißner-Ochsenfeld-Effekt nachgewiesen
und nicht über das Verschwinden des elektrischen Widerstands.
Trifft eine elektromagnetische Welle auf einen Supraleiter, so dringt diese etwas in den Supraleiter ein und regt sowohl Cooper-Paare als auch ungepaarte Elektronen zu Bewegungen an.
Dadurch wird der Widerstand des Supraleiters endlich und mit zunehmender Frequenz grösser.
3 Anwendungen
Das Erzeugen von starken Magnetfeldern mit supraleitenden Spulen, verlustlose Stromleitung
und damit auch induktive Energiespeicherung sind natürlich naheliegende technische Anwendungen. Diese sind aber zur Zeit noch nicht so weit für den gross angelegten technischen Einsatz
z. B. für die elektrische Energieverteilung (Leitungen, Transformatoren, elektrische Motoren)
ausgereift. Supraleiter zweiter Art verhalten sich nämlich nach dem Übergang vom supraleitenden zum „normal leitenden“ Zustand, z. B. beim überschreiten der maximalen Stromdichte, wie
Isolatoren. Sollte dies geschehen, so wird der durch die Leitungsinduktivität aufrecht erhaltene
Strom das Material durch dissipative Leistung unter Umständen zerstören16 . Als Gegemassnahme kann beispielsweise der Supraleiter in Form von mikroskopisch dünnen Fäden in einen
normalen Leiter eingebettet werden, welcher im Notfall die Stromleitung übernehmen kann.
Allgemein ist (zur Zeit noch) die Schwierigkeit, neben der effizienten Kühlung, aus keramikhaltigen Materialien Drähte und Leitungen (kostengünstig) herzustellen.
Allerdings werden starke Magnetfelder standardmässig mit supraleitenden Spulen erzeugt.
Spulen sind räumlich begrenzt, so dass eine effiziente Kühlung möglich ist.
• MRT (Magnetresonanztomographie) oder MRI (Magnetic Resonance Imaging)
Quelle: http://de.wikipedia.org/wiki/Magnetresonanztomographie
Bemerkung: Für die MRT werden nicht zwingend supraleitende Spulen benötigt, da die erforderlichen magnetischen Felder nur etwa 3 T betragen. Aus energie-ökonomischen Gründen lohnt sich deren Einsatz dennoch.
• Kern(spin)resonanzspektroskopie oder NMR (Nuclear Magnetic Resonance)
Diese Anwendung benötigt magnetische Felder von bis zu 20 T, was die Benutzung von
supraleitenden Spulen aus energie-wirtschaftlichen Gründen naheliegt.
Quelle: http://de.wikipedia.org/wiki/Kernspinresonanzspektroskopie
• Ablenk- und Fokussierspulen für Protonen- oder Elektronenstrahlen (z. B. beim Large
Hadron Collider im Cern, http://public.web.cern.ch/public/en/LHC/LHC-en.html)
• Magnetlager (http://de.wikipedia.org/wiki/Supraleitendes_Magnetlager): Entsprechend dem
Meißner-Ochsenfeld-Effekt erzeugt die Anwesenheit eines extern induzierten Magnetfeldes im Supraleiter Wirbelströme, welche ein Gegenfeld erzeugen. Dadurch entstehen
16
Dabei wird auch das Kühlmittel (flüssiges Helium oder Stickstoff) möglicherweise explosionsartig verdampfen.
6
3 Anwendungen
abstossende Kräfte zwischen Supraleiter und externem Magneten mit denen eine inhärent stabile und reibungsfreie Lagerung erzeugt werden kann (Anwendungsbeispiel:
http://www.iem.ing.tu-bs.de/paper/2004/hompa_04.htm).
Supraleitung ist ausserdem zur Realisierung von Spannungs- und Widerstandsnormalen, sowie von empfindlichen Detektoren von grosser technischer Bedeutung. Diese Phänomene sind
quantenmechanischer Natur und finden nur bei extrem niedrigen Temperaturen statt.
• Der Josephson-Effekt17 erlaubt es Spannungen mit einer relativen Unsicherheit von
1 : 1010 (1 nV pro 10 V) reproduzierbar zu erhalten. Ein Josephson-Element besteht aus
zwei Supraleitern, welche durch eine isolierende Schicht von einigen Nanometern getrennt
sind. Wird so ein Element mit einer Mikrowelle bestrahlt, so wird eine Spannung zwischen
den beiden Supraleitern erzeugt18 . Dabei herrscht Proportionalität zwischen der Frequenz
f und der Spannung Un . Diese hängt nur vom Verhältnis der Plank’schen Konstante h
und der Elementarladung e ab:
Un = n
h
1
f
f =n
2e
KJ90
für
n = 1, 2, 3, · · ·
(6)
Der Wert der Josephson-Konstante: KJ90 = 483’597.9 GHz/V wurde in 1990 international
vereinbart. Er ist demzufolge als exakt zu betrachten.
Beispiel: Bei einer Frequenz von 70 GHz ergibt sich die Spannung U1 = 144.75 µV.
Diverse metrologische Institute bieten Spannungsnormale an, welche elektrische Spannungen bis zu 10 V mit einer Auflösung von 1 nV zu Eich- und Kalibrierzwecken abgeben
können.
• Supraleitende Quanteninterferenzeinheiten oder SQUID (Superconducting Quantum
Interference Device) werden zur Messung von extrem schwachen magnetischen Feldern,
beziehungweise winzigen magnetsichen Flüssen, benutzt. Der prinzipielle Aufbau und die
Funktionsweise eines SQUID ist in Abbildung 4 dargestellt. Damit können Änderungen
des magnetischen Flusses durch die Fläche des Rings detektiert werden: eine Veränderung des magnetischen Flusses um ein einziges magnetisches Flussquantum, wie in der
Beziehung (5) definiert, führt zu einer Periode in der modulierten Amplitude des sonst
konstanten Josephson-Stroms. Durch verwenden eines zusätzlichen supraleitenden „Transformators“ kann die Empfindlichkeit eines SQUIDs so gesteigert werden, dass damit Messungen von magnetischen Feldern im Bereich von 10−15 T möglich sind. SQUIDS werden
unter anderem in der Medizinaltechnik benutzt, um Stromstärken im menschlichen Körper, wie z. B. Hirnströme, zu messen. Ebenfalls in der Medizinaltechnik können sie zur
Detektion von Kerspinresonanzen bei niedrigen Magnetfeldstärken (MRT) benutzt werden.
Quelle: http://de.wikipedia.org/wiki/SQUID
• Der Josephson-Effekt und die SQUIDS haben weitere, wichtige technische Anwendungen
ermöglicht, wie zum Beispiel diverse hochempfindliche Detektoren19 für Photonen
(elektromagnetische Wellen vom Ferninfrarot bis zu Röntgen- oder Gammastrahlen) und
17
18
19
durch Brian David Josephson (1940 - ) in 1962 theoretisch vorausgesagt
Der Effekt ist auch umkehrbar.
Diese Detektoren gehören zu den empfindlichsten Sensoren überhaupt.
7
3 Anwendungen
Abbildung 4: Ein SQUID besteht aus einem supraleitenden Ring welcher durch zwei dünne isolierende Stellen (Josephson-Kontakte) unterbrochen wird. Ändert sich der Fluss
des Magnetfelds durch den Ring, so wird (im Ring) ein Strom induziert, der zu
einer (beinahe harmonischen) Modulation der Amplitude des Gleichstroms führt.
Jede Periode entspricht dabei einer Magnetfeldänderung um ein Flussquantum,
Es gibt auch SQUIDs mit nur einem Josephson-Kontakt, welche mit Wechselstrom betrieben werden.
Bildquelle: http://de.wikipedia.org/wiki/Benutzer:Herbertweidner
8
Literatur
andere Teilchen, insbesondere Bolometer und Kalorimeter {für mehr Information cf. z. B.
(1) Buckel, Kleiner}.
• Filter für die Kommunikationstechnik
Moderne Kommunikationssysteme wie UMTS, arbeiten im Frequenzbereich von einigen
GHz. Dafür werden schmalbandige Bandpassfilter hoher Güte benötigt. Diese können
dank supraleitenden Resonatoren (LC-Schwingkreise) kleiner gemacht werden als solche
aus normalleitenden Metallen {zusätzliche Information findet man in (1) Buckel, Kleiner}.
• Der Quanten-Hall-Effekt20 erlaubt es Widerstandswerte mit einer relativen Unsicherheit von 1 : 109 (1 mΩ pro 1 MΩ) reproduzierbar zu erhalten21 . Der Hall-Widerstand
ist beim Hall-Element durch das Verhältnis der Hall-Spannung zur Stromstärke im HallPlättchen definiert. Dieser ist im klassischen Fall proportional zur Stärke des magnetischen Felds, welches senkrecht zum Plättchen steht. Beim Quanten-Hall-Effekt weist der
Widerstand bei zunehmender Stärke des magnetischen Felds ausgeprägte Plateaux auf,
bei denen er konstant und unabhängig von der Magnetfeldstärke und den Eigenschaften
des Plättchens, d. h. Geometrie und Material ist (cf. Abbildung 5). Diese quantisierten
Widerstandswerte hängen nur von der Plank’schen Konstante h und der Elementarladung
e ab:
h
RK
RH = 2 =
für
n = 1, 2, 3, · · ·
(7)
ne
n
Der Wert der Klitzing-Konstante: RK = 25’812.807 Ω90 wurde in 1990 international vereinbart. Er ist demzufolge als exakt zu betrachten. Der Index n bestimmt das Plateau.
Basierend auf dem Quanten-Hall-Effekt können Widerstandsnormale zwischen 1 Ω und
13 kΩ mit einer Messunsicherheit von 1 : 2 · 108 realisiert werden22 .
Bemerkung: Der Quanten-Hall-Effekt ist, obschon zur Tieftemperaturphysik gehörend,
kein Effekt in dem Supraleitung eine Rolle spielt. Er wird hier nur als dazu passende
Ergänzung vorgestellt.
Literatur
[1] Werner Buckel, Reinhold Kleiner: Supraleitung Grundlagen und Anwendungen, Wiley-VCH,
2004, ISBN-13: 978-3-527-40348-6, Preis: e 72.90, CHF 117.[2] Paul Allen Tipler, Gene Mosca: Physik für Wissenschaftler und Ingenieure, Spektrum Akademischer Verlag, 2004, ISBN: 978-3-8274-1164-8, Preis: CHF 121.Ein kurzes Kapitel ist in diesem umfassenden Werk der Supraleitug gewidmet.
20
21
22
durch Klaus von Klitzing (1943 - ) in 1980 bei der Untersuchung von MOS-Feldeffekt-Transistoren entdeckt
bei Temperaturen unterhalb 1 K und Magnetfeldstärken von einigen T, welche mit supraleitenden Spulen
realisiert werden
Quelle: EJPD, Bundesamt für Metrologie METAS, Sektion Elektrizität, Stand 2009
9
Literatur
Abbildung 5: Die treppenartige Kurve zeigt den Verlauf des Hall-Widerstands RH in Funktion der magnetischen Feldstärke B bei Temperaturen unterhalb 2 K. Der Index i
entspricht hier dem Index n im Text. Das Plateau bei n = 1 ist bei noch grösseren Feldstärken zu finden (oberhalb 17 T) und ausserhalb der Massstäbe der
vorliegenden Figur. Die gezackte Kurve beschreibt den Verlauf des Leitungswiderstands, welcher bei jeder Stufe verschwindet.
Bildquelle: http://nobelprize.org/nobel_prizes/physics/laureates/1998/press.html
10