- dieter

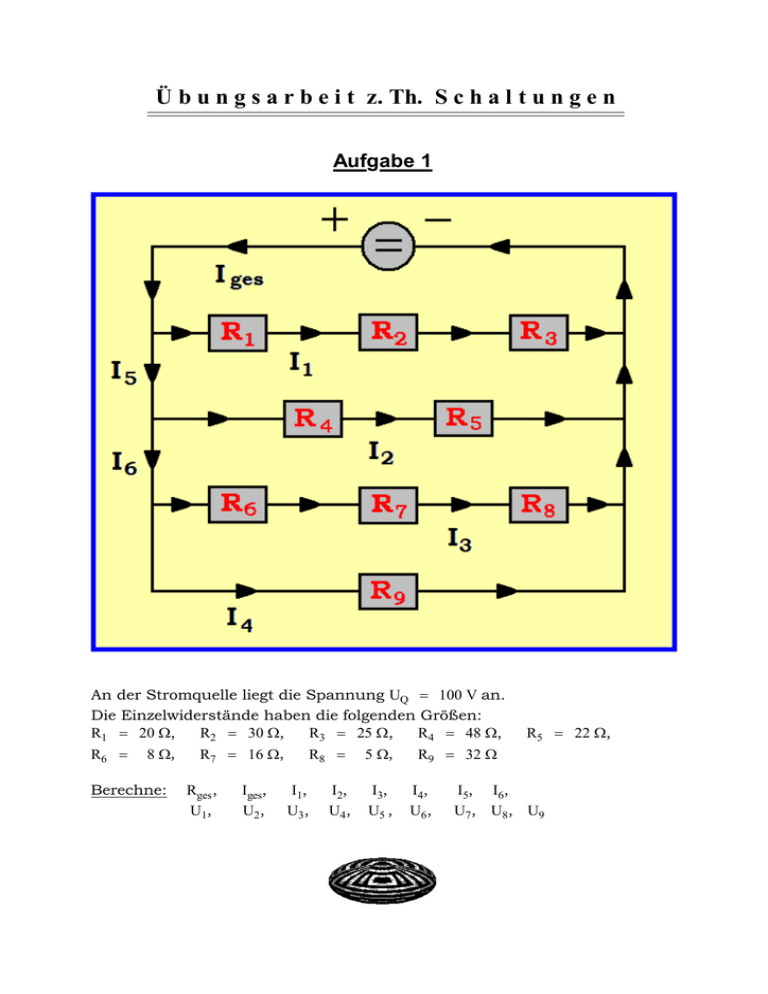
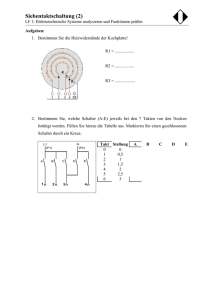
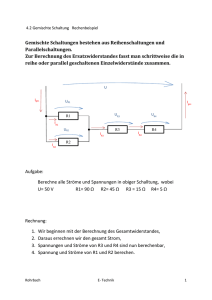
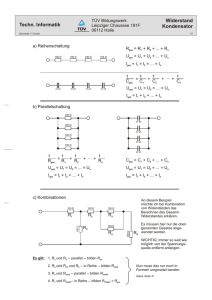
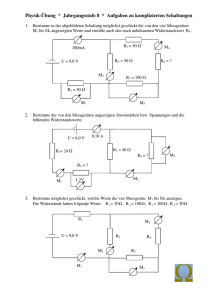
Ü b u n g s a r b e i t z. Th. S c h a l t u n g e n
Aufgabe 1
An der Stromquelle liegt die Spannung UQ = 100 V an.
Die Einzelwiderstände haben die folgenden Größen:
R1 = 20 Ω,
R2 = 30 Ω,
R3 = 25 Ω,
R4 = 48 Ω,
R6 = 8 Ω,
R7 = 16 Ω,
R8 = 5 Ω,
R9 = 32 Ω
Berechne:
Rges ,
U1,
Iges,
U2,
I1,
U3,
I2,
U4,
I3,
U5 ,
I4,
U6,
R5 = 22 Ω,
I5, I6,
U7, U8, U9
Aufgabe 2
Gegeben:
U1
=
150 V,
R2
=
40 Ω,
R3
=
20 Ω,
Berechne:
Iges, I3, UQ, UAB , R , R
1
ges
I2
=
3A
Aufgabe 3
Gegeben:
R1 = 40 Ω, R4 = 60 Ω, UQ = 74 V, Iges = 0,5 A, I3 = 0,3 A
Berechne:
I2,
UAB,
R2,
R3,
Rges
Aufagbe 4
Gegeben:
R1 = 54 Ω,
R2 = 30 Ω,
R3 = 40 Ω,
R4 = 70 Ω
a) Wie groß muss der Widerstand Ry gewählt werden, damit durch
den Widerstand Rx kein Strom fließt ?
b) Berechne für den Fall, dass durch Rx kein Strom fließt und die
Stromstärke Iges = 5 A beträgt,
1. den Gesamtwiderstand der Schaltung.
2. die spannung UQ an der Stromquelle.
3. die Stromstärken I1,2 und I3,y,4
L ö s u n g e n
Aufgabe 1
R1,2,3
=
R1 + R2 + R3
=
R4,5
=
R4 + R5
=
R6,7,8
=
R6 + R7 + R8
R1,2,3,4,5
=
R6,7,8,9
=
Rges
=
=
75 Ω
48 Ω + 22 Ω
=
70 Ω
=
8 Ω + 16 Ω + 5 Ω
=
29 Ω
R1,2,3 ⋅ R4,5
R1,2,3 + R4,5
=
75 Ω ⋅ 70 Ω
75 Ω + 70Ω
=
5250 Ω 2
145 Ω
≈ 36,207 Ω
R6,7,8 ⋅ R9
R6,7,8 + R9
=
29 Ω ⋅ 32 Ω
29 Ω + 32 Ω
=
928 Ω 2
61 Ω
≈ 15,213 Ω
=
32,207 Ω ⋅ 15,213 Ω
32,207 Ω + 15,213 Ω
≈
10,712 Ω
R1,2,3,4,5 ⋅ R6,7,8,9
R1,2,3,4,5 + R6,7,8,9
20 Ω + 30 Ω + 25Ω
Die Schaltung hat den Gesamtwiderstand Rges = 10,712 Ω.
UQ
100 V
=
≈ 9,335 A
Rges
10 712 Ω
Die Gesamtstromstärke Iges beträgt Iges = 9,335 A.
Iges =
I1 =
UQ
100 V
=
≈ 1,333 A
R1,2,3
75 Ω
Die Stromstärke I1 beträgt
I2 =
Die Stromstärke I2 beträgt
I1 = 1,333 A.
I3 =
UQ
=
R6,7,8
100 V
≈ 3,448 A
29 Ω
Die Stromstärke I3 beträgt
I3 = 3,448 A.
I5 = Iges − I1 = 9,335 A − 1,333 A
= 8,002 A
Die Stromstärke I5 beträgt
I5 = 8,002 A.
UQ
100 V
=
≈ 1,429 A
R4,5
70 Ω
I2 = 1,429 A.
I4 =
UQ
100 V
=
= 3,125 A
R9
32 Ω
Die Stromstärke I4 beträgt
I4 = 3,125 A.
I6 = I5 − I2 = 8,002 A − 1,429 A
= 6,573 A
Die Stromstärke I6 beträgt
I6 = 6,573 A.
Fortsetzung von Aufgabe 1
Es gilt: U1 + U2 + U3
=
UQ
=
100 V
und
=
R1 : R2 : R3
=
20 : 30 : 25
U1
=
100 V ⋅ 4
15
≈
26,667 V
U2
=
100 V ⋅ 6
15
=
40 V
U3
=
100 V ⋅ 5
15
≈
33,333 V
U1 : U2 : U3
=
4:6:5
Die Spannungen U1, U2 und U3 betragen: U1 = 26,667 V, U2 = 40 V
und U3 = 33,333 V.
Es gilt:
U4 + U5
=
UQ
=
100 V
U4 : U5
=
R4 : R5
=
48 : 22
U4
=
100 V ⋅ 24
35
≈
68,517 V
U5
=
100 V ⋅ 11
35
≈
und
=
24 : 11
31,429 V
Die Spannungen U4 und U5 betragen: U4 = 68,571 V und U5 = 31,429 V
Es gilt: U6 + U7 + U8
=
UQ
=
100 V
und
=
R6 : R7 : R8
=
8 : 16 :5
U6
=
100 V ⋅ 8
29
≈
27,586 V
U7
=
100 V ⋅ 16
29
≈
55,172 V
U8
=
100 V ⋅ 5
29
≈
17,241 V
U6 : U7 : U8
Die Spannungen U6, U7 und U8 betragen:
U6 = 27,586 V, U7 = 55,172 V
und U8 = 17,241 V
Da der Eingang des Widerstandes R9 direkt mit dem Pluspol der Stromquelleund der Ausgang direkt mit dem Minuspol verbunden ist, hat die Spannung U9
denselben Wert wie die Spannung UQ; also U9 = 100 V.
Aufgabe 2
UAB = I2 ⋅ R2 = 3 A ⋅ 40 Ω = 120 V
Die Spannung zwischen den Punkten A und B beträgt UAB = 120 V.
UQ = UAB + U1 = 120 V + 150 V = 270 V
Die Spannung an der Stromquelle beträgt UQ = 270 V.
Die Spannung UAB = 120 V liegt auch am Widerstand R3. Daraus folgt:
UAB
120 V
=
= 6A
I3 =
R3
20 Ω
Durch den Widerstand R3 fließt ein Strom der Stärke I3 = 6 A.
Iges = I2 + I3 = 3 A + 6 A = 9 A
Die Stromstärke Iges beträgt Iges = 9 A.
UQ
270 V
=
= 30 Ω
Iges
9A
Die Schaltung hat den Gesamtwiderstand Rges = 30 Ω.
Rges =
R2 ⋅ R3
40 Ω ⋅ 20 Ω
800 Ω 2
1
=
= 13 Ω
3
40 Ω + 20 Ω
60 Ω
R2 + R3
1
2
Rges = R2,3 + R1 ⇔ R1 = Rges − R2,3 = 30 Ω − 13 Ω = 16 Ω
3
3
2
Der Widerstand R1 hat die Größe R1 = 16 Ω.
3
R2,3 =
=
Aufgabe 3
Iges = I2 + I3
⇔
I2 = Iges − I3 = 0,5 A − 0,3 A = 0,2 A
Die Stromstärke I2 beträgt I2 = 0,2 A.
Rges =
UQ
74 V
=
= 148 Ω
Iges
0,5 A
Die Schaltung hat den Gesamtwiderstand Rges = 148 Ω.
R1,4 = R1 + R4 = 40 Ω + 60 Ω = 100 Ω
Rges = R1,4 + R2,3
⇔
R2,3 = Rges − R1,4 = 148 Ω − 100 Ω = 48 Ω
U1 : UAB : U4 = R1 : R2,3 : R4 = 40 : 48 : 60 = 10 : 12 : 15
74 V ⋅ 12
UAB =
= 24 V
37
Die Spannung UAB beträgt UAB = 24 V.
Fortsetzung von Aufgabe 3
R2 =
UAB
24 V
=
= 120 Ω
I2
0,2 A
Der Widerstand R2 beträgt R2 = 120 Ω.
R3 =
UAB
24 V
=
= 80 Ω
I3
0,3 A
Der Widerstand R3 beträgt R3 = 80 Ω.
Aufgabe 4
a) Wenn durch Rx kein Strom fließt, so gilt: Ux = 0
Die Spannung die über R1 abfällt ist dann gleich der Spannung, die
über R3,y = R3 + Ry abfällt; und die Spannung, die über R2 abfällt, ist
gleich der Spannung, die über R4 abfällt.
Da die Spannungen proportional zu den Größen der Widerstände sind,
an denen sie anliegen, gilt:
R3 + Ry
R4
=
R1
R2
⇔
Ry
=
R1
⋅ R4 − R3
R2
=
54 Ω
⋅ 70 Ω
30 Ω
=
86 Ω
Damit durch Rx kein Strom fließt muss Ry = 86 Ω betragen.
b) 1. Die Größe des Widerstandes Rx hat für den Gesamtwiderstand der
Schaltung keine Bedeutung, da ja durch Rx kein Strom hindurchfließt.
Der Gesamtwiderstand ist folglich nur durch die 5 Einzelwiderstände
R1, R2 , R3, Ry und R4 festgelegt.
R1,2
=
R1 + R2
=
54 Ω + 30 Ω
=
84 Ω
R3,y,4
=
R3 + Ry + R4
=
40 Ω + 86 Ω + 70 Ω
=
196 Ω
Rges
=
R1,2 ⋅ R3,y,4
R1,2 + R3,y,4
=
84 Ω ⋅ 196 Ω
84 Ω + 196 Ω
=
58,8 Ω
Die Schaltung hat den Gesamtwiderstand Rges = 58,8 Ω.
2. UQ = Rges ⋅ Iges = 58,8 Ω ⋅ 5 A = 294 V
Zwischen den Polen der Stromquelle liegt die Spannung UQ = 294 V.
Fortsetzung von Aufgabe 4
3. I1,2 =
UQ
294 V
=
= 3,5 A
R1,2
84 Ω
Durch die Widerstände R1 und R2 fließt der Strom I1,2 = 3,5 A.
I3,y,4 = Iges − I1,2 = 5 A − 3,5 A = 1,5 A
Durch die Widerstände R3, Ry und R4 fließt der Strom I3,y,4 = 1,5 A.