Carnotprozess = idealer Kreisprozess

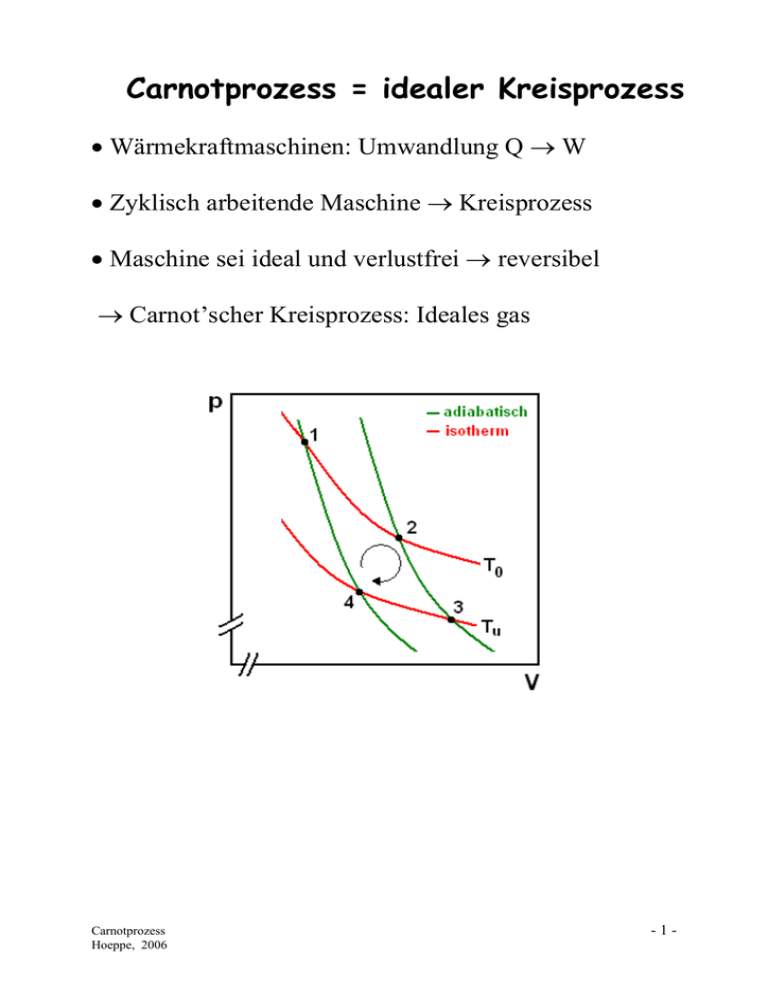
Carnotprozess = idealer Kreisprozess
• Wärmekraftmaschinen: Umwandlung Q → W
• Zyklisch arbeitende Maschine → Kreisprozess
• Maschine sei ideal und verlustfrei → reversibel
→ Carnot’scher Kreisprozess: Ideales gas
Carnotprozess
Hoeppe, 2006
-1-
Carnotprozess: Einzelschritte
1 → 2:
Wärmezufuhr: isotherme Expansion bei T = T0
Q12 = −W12 = nRT0 ln
2 → 3:
V2
V1
keine Wärmezufuhr: adiabatische Expansion
W23 = ∆U 23 = ncV ∆T23 = ncV (Tu − T0 )
3 → 4:
Wärmeabgabe: isotherme Kompression bei T = Tu
Q34 = −W34 = nRTu ln
4 → 1:
V4
V3
keine Wärmezufuhr: adiabatische Kompression
W41 = ∆U 41 = ncV ∆T41 = ncV (T0 − Tu )
Carnotprozess
Hoeppe, 2006
-2-
Carnotprozess: Energiebilanz Kreisprozess
Wges = W12 + W23 + W34 + W41
V1
V
+ ncV (Tu − T0 ) − nRTu ln 4 + ncV (T0 − Tu )
V2
V3
V
V
= Q12 + W34 = − nRT0 ln 1 + nRTu ln 4
V2
V3
Wges = nRT0 ln
Qges
∆U ges = Wges + Qges = 0
(→ 1. HS, ok ! )
Wirkungsgrad:
Verhältnis zugeführter Wärme zu erhaltener Arbeit η :
η :=
Wges
Q12
V1
V
− nRTu ln 4
V2
V3
V
nRT0 ln 1
V2
nRT0 ln
=
Für Adiabaten gilt T⋅V κ-1 = const. →
T0V2
κ −1
κ −1
T0V1
= TuV3
= TuV4
κ −1
κ −1
η :=
→
→
Wges
Q12
T0 ⎛ V3 ⎞
=⎜ ⎟
Tu ⎜⎝ V2 ⎟⎠
κ −1
κ −1
T0 ⎛ V4 ⎞
=⎜ ⎟
Tu ⎜⎝ V1 ⎟⎠
=
T0 − Tu
T0
V3 V4
=
V2 V1
bzw.
V4 V1
=
V3 V2
η < 1 da Tu > 0 !
Der Wirkungsgrad einer realen Maschine ist ≤ ηCarnot !
Carnotprozess
Hoeppe, 2006
-3-
→ Schlussfolgerung:
Damit eine Maschine zyklisch arbeiten kann, muss ein Teil der
zugeführten Wärme wieder abgegeben werden. Da Tu = 0
unmöglich gilt immer η < 1.
2. HS der Thermodynamik:
Es existiert kein Perpetuum Mobile 2. Art,
d.h. keine Maschine, die nichts weiter tut als Wärme
in Arbeit umzuwandeln.
(Eine genauere Analyse der Wärmen führt zum Begriff
der „reduzierten Wärme“ bzw. der „Entropie“. Eine andere
Formulierung des 2. HS ist die Aussage, dass die Entropie
in abgeschlossenen Systemen nur zunehmen aber nie abnehmen kann.
Hier zeigt sich die Besonderheit der Energieform ’Wärme’, d.h. die
ungeordnete Bewegung der Moleküle lässt sich nicht einfach in geordnete
Bewegung (Arbeit) umwandeln.)
Carnotprozess
Hoeppe, 2006
-4-