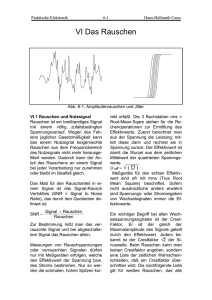
1/f Rauschen

NANO III
Rauschen
in elektronischen Signalen
08.04.2004
H.Hidber
1
Rauschen allgemein 1
• „Noise“ im weitesten Sinne ist: jede unerwünschte
Störung, welche das gewünschte Signal stört und
verfälscht.
Im deutschsprachigen Raum wird zwischen Störsignalen und
Rauschen unterschieden:
• Rauschen: zufällige Fluktuationen, welche eine genauere Messung
der Signale verunmöglichen. Rauschen ist oft durch grundlegende
physikalische Prozesse bedingt und limitiert die Genauigkeit.
• Störsignale: werden durch externe Systeme kapazitiv, magnetisch
oder galvanisch (über Erdschlaufen) eingekoppelt. Diese Störungen
können durch Massnahmen reduziert oder verhindert werden.
08.04.2004
H.Hidber
2
Rauschen allgemein 2
Eine Gleichspannung soll gemessen werden:
Zusätzlich zum stabilen Mittelwert werden bei hoher Auflösung noch
folgende störende Anteile sichtbar:
• Rauschen: zufällige Fluktuationen, welche ohne wiederkehrende
Periode völlig zufällig vom Wert abweichen.
• Störsignale: der periodische Anteil, welcher in einem bestimmten
Rhythmus wiederkehrt (hier die sinusförmige Störung von 50 Hz).
08.04.2004
H.Hidber
3
Thermisches Rauschen 1
Ladungsträger oberhalb des absoluten Temperaturnullpunkts befinden
sich in zufälliger Brown‘scher Bewegung, dadurch erzeugen sie eine
zufällige Fluktuation der Spannung am Leiter. Da diese
Schwankungen ausser von physikalischen Konstanten nur von der
Grösse des Widerstandes und der absoluten Temperatur abhängig
sind, nennt man dieses Rauschen: „Das thermische Rauschen“.
Dieses Phänomen kann durch eine in Serie zum Widerstand R
geschaltete Rausch-Spannungsquelle ur in Veff beschrieben werden:
ur =
4 kTR ∆ f
wobei k = Bolzmann Konstante = 1.38 x 10-23 Ws/K, T = absolute
Temperatur in K, R = el.Widerstand in Ohm (V/A), ∆f = Bandbreite des
Rauschens in Hz.
Merke: Ein Widerstand von 1 kOhm rauscht bei einer Bandbreite von
1Hz und bei Zimmertemperatur mit 4nV (effektiv)!
08.04.2004
H.Hidber
4
Thermisches Rauschen 2
Das thermische Rauschen wird oft auch nach seinen Entdeckern
genannt:
Johnson Rauschen (experimenteller Nachweis, Phys.Rev. 32, 97-109 (1928))
oder
Nyquist Rauschen (theoretische Herleitung, Phys.Rev. 32, 110-113 (1928)).
Die Rauschleistung ist unabhängig vom Widerstand:
2
u
Pr = r =
R
(
4 kTR ∆ f
R
)
2
= 4 kT ∆ f
Die Leistungsdichte pro Hz wird:
Pr
= 4 kT
∆f
wobei k = Bolzmann Konstante = 1.38 x 10-23 Ws/K, T = absolute
Temperatur in K, ∆f = Bandbreite des Rauschens in Hz.
08.04.2004
H.Hidber
5
Thermisches Rauschen 3
Das thermische Rauschen ist ein sogenanntes weisses Rauschen,
d.h. die Rauschdichte ist unabhängig vom Frequenzintervall.
Die auftretenden Amplituden gehorchen dabei der Gauss‘schen
Normalverteilung.
weisses Rauschen
08.04.2004
H.Hidber
Häufigkeit der
momentanen Werte
6
Rauschbandbreite 1
Die interessanten Frequenzbereiche der Signale und das darin
enthaltene Rauschen können nur gemeinsam verstärkt werden.
Zur Berechnung der Bandbreite gelten für die Signale und das
Rauschen aber unterschiedliche Definitionen:
Die Grenzfrequenz für Signale f2(-3dB Frequenz) wird erreicht, wenn
die Leistung des Signals Ps auf ½ des maximalen Wertes gesunken
ist:
Ps
Us
Ps
1
1 oder
für Spannungen:
=
=
=
= 0.707
Pmax
2
U max
Pmax
2
Das Produkt Rauschbandbreite ∆f mal Quadrat der max. Spannungsverstärkung beinhaltet die gesamte Fläche mit dem Quadrat der
Spannungs-verstärkung zu Frequenz Kurve. Oder aufgelöst nach ∆f:
∆f =
08.04.2004
∞
1
Au max
2
∫ A (f )
u
2
df
0
H.Hidber
7
Rauschbandbreite 2
Je nachdem wie steil der Abfall bei hohen Frequenzen gewählt wird,
differieren Signal- und Rauschbandbreite beträchtlich:
Filtertyp (entkoppelt)
Tiefpass 1.Ordnung
Tiefpass 2.Ordnung
Tiefpass 3.Ordnung
08.04.2004
Rausch-/Signal-bandbreite
1.571
1.222
1.155
H.Hidber
8
1/f Rauschen 1
1/f Rauschen wird auch als Excess Noise (Excess = Überschuss)
oder Tieffrequenz Rauschen bezeichnet.
Es entsteht zusätzlich zum thermischen Rauschen in stromdurchflossenen Materialien mit körniger Struktur, Halbleitern mit
nichtperfektem Gitter oder dünnen Filmen. Kohlewiderstände zeigen
dieses Zusatzrauschen, nicht jedoch Metallfilm-Widerstände!
Das Leistungsspektrum des 1/f Rauschens zeigt, dass die
Leistungsdichte linear zunimmt, bei linear abnehmender Frequenz.
Dies bedeutet das die Rauschspannung mit der Wurzel der
abnehmenden Frequenz ansteigt.
1/f Rauschen
10
1
0.1
1
10
100
1000
10000
Frequenz in [Hz]
08.04.2004
H.Hidber
9
1/f Rauschen 2
1/f Rauschen entsteht zusätzlich zum thermischen Rauschen. Bei
hohen Frequenzen ist die 1/f Komponente klein, das Gesamtrauschen
wird durch das thermische frequenzunabhängige Rauschen dominiert.
Bei tiefen Frequenzen ist dagegen das 1/f Rauschen dominant.
Dies bedeutet: Bei Anwesenheit von 1/f Rauschen kann die
Messgenauigkeit eines Gleichspannungssignals nicht durch
Verlängerung der Messzeit verbessert werden!
10
1
0.1
1
10
1/f
08.04.2004
100
thermis ch
H.Hidber
1000
10000
1/f + thermis ch
10
Weisses ÅÆ rosa Rauschen
Sind alle Frequenzen im Rauschspektrum gleich stark vertreten, so
spricht man – in Analogie zum Spektrum des sichtbaren Lichts - von
weissem Rauschen.
weisses Rauschen
Steigen die Rauschamplituden bei tiefen Frequenzen an, so könnte
man – wieder in Analogie - von rotem Rauschen sprechen.
Beim 1/f Rauschen erfolgt der Anstieg aber nur mit der Wurzel der
abnehmenden Frequenz. Der Verlauf liegt zwischen der Kurve für
weisses und rotes Rauschen. Zwischen Weiss und Rot liegt Rosa.
Deshalb wird hier von rosa Rauschen gesprochen.
rosa Rauschen
08.04.2004
H.Hidber
11
Schrot Rauschen
Fliesst ein Strom in Dioden, Transistoren oder Vakuum-Röhren, tritt
durch zu überwindenden Barrieren ein Rauschmechanismus ein,
welcher Schrot Rauschen (Shot Noise) genannt wird. Der Strom in
diesen Bauteilen ist nicht kontinuierlich, die Ladungsträger treffen z.B.
als einzelne Ladungspulse auf die Elektrode und verursachen ein
prasselndes Rauschen. Zu vergleichen mit dem Aufprallen von Regen
oder Körnern auf einer Membrane. Da dies ein stochastischer Prozess
ist, sind alle Frequenzen gleich häufig, das Rauschen hat ein
konstantes Spektrum; d.h. es ist weisses Rauschen.
Der Effektivwert des entstehenden Rauschstromes berechnet sich:
ish =
2 qI DC ∆ f
wobei
q = elektrische Einzel-Ladung = 1.602 x 10-19 As (As = Coulomb),
IDC = der fliessende Gleichstrom in A und
∆f = Rauschbandbreite in Hz (Hz = 1/s)
08.04.2004
H.Hidber
12
Popcorn Rauschen
Metallische Verunreinigungen können in Halbleitern Burst Noise oder
Popcorn Rauschen erzeugen. Das Rauschen kann durch
Verbesserung der Prozesse bei der Herstellung minimiert werden. Das
Rauschen erscheint auf einem Oszilloskop als Impulse mit fester
Amplitude aber zufälliger Dauer und Wiederholungsrate. Auf einem
Lautsprecher tönt dieses Rauschen wie das Zerplatzen der Maiskörner
beim Herstellen von Popcorn, deshalb auch der Name.
08.04.2004
H.Hidber
13
Addition von Rauschquellen 1
Serieschaltung
R1
u1
R0
R2
u2
u0
Die beiden rauschfreien Widerstände R1 und R2 mit
den dazugehörenden thermischen Rauschquellen
u1 und u2 sollen zur Ersatzschaltung mit dem
rauschfreien Widerstand R0 und der dazugehörenden thermischen Rauschquelle u0 vereinfacht
werden.
Der Gesamtwiderstand ist gleich der Summe der
Teilwiderstände:
R0 = R1 + R 2
Da die zwei Rauschquellen voneinander
unabhängiges Rauschen generieren sind deren
Leistungen zu addieren :
u =u +u
2
0
2
1
2
2
damit ergibt sich für die Gesamtrauschspannung:
u0 = u + u
2
1
08.04.2004
H.Hidber
2
2
14
Addition von Rauschquellen 2
Die beiden rauschfreien Widerstände R1
und R2 mit den dazugehörenden
thermischen Rauschquellen u1 und u2
werden zuerst in die gleichwertige
Schaltung mit parallelen RauschStromquellen i1 und i2 umgewandelt.
Parallelschaltung
R1
R2
u1
u2
R1
i1
08.04.2004
R2
i2
u
i1 = 1 =
R1
4 kTR 1 ∆ f
=
R1
4 kT ∆ f
R1
u2
i2 =
=
R2
4 kTR 2 ∆ f
=
R2
4 kT ∆ f
R2
H.Hidber
15
Addition von Rauschquellen 3
Nun können alle Elemente parallel
geschaltet werden und zur Ersatzschaltung
mit dem rauschfreien Widerstand R0 und
der dazugehörenden thermischen
Rauschstromquelle i0 vereinfacht werden.
Der Gesamtwiderstand ist:
Parallelschaltung
R1
i1
R2
i2
R1 R 2
R0 =
R1 + R 2
Da die zwei Rauschquellen voneinander
unabhängiges Rauschen generieren sind
deren Leistungen zu addieren:
i02 = i12 + i22
R0
R0
i0
u0
damit ergibt sich für den Rauschstrom i0
und die Rauschspannung u0:
i0 = i12 + i22
2
u 0 = R0 i0 = R0 i12 + i22 = R0
08.04.2004
H.Hidber
 u1   u 2 
  + 

 R1   R 2 
16
2
Verstärkerrauschen 1
rauschfreier
Widerstand
R0
Signal
us
ur
Rauschspannungquelle
des Verstärkers
uv
Rauschquelle
von R0
rauschfreier
Verstärker
iv
Rauschstromquelle
des Verstärkers
Das Signal Us soll verstärkt werden Die Signalquelle hat einen inneren
Widerstand R0. Also muss das Rauschen des Quellenwiderstandes in die
Berechnung einbezogen werden. Dazu wird der Widerstand als rauschfrei
angenommen und sein Rauschen mit der Rauschspannungsquelle ur
berücksichtigt. Der Verstärker produziert zusätzliches Rauschen. Aber auch
hier wird der Verstärker rauschfrei angenommen. Sein Rauschen wird in die
Rauschspannungsquelle uv und in die Rauschstromquelle iv verlagert.
Die gesamte Rauschspannung am Eingang des Verstärkers beträgt:
u gesamtRaus chen = u + u + i R
2
r
08.04.2004
H.Hidber
2
v
2
v
2
0
17
Verstärkerrauschen 2
Das Rauschen der Verstärkerschaltung wird bei kleinem Quellenwiderstand
durch das Spannungsrauschen, bei hohen Quellwiderständen durch das
Stromrauschen dominiert. Nur im mittleren Bereich sinkt das Rauschen ans
physikalische Minimum, nämlich optimal nahe an das thermische Rauschen.
10000
Rauschen in Abhängigkeit des Widerstands der Quelle mit
Operationenverstärker LT1007
Rauschen in nV/sqrt(Hz)
1000
100
10
Thermisch Ur
Verstärker Uv
Verstärker Ir x R0
1
Gesamt U
0.1
0.01
0.001
0.0001
1.E+00
1.E+01
1.E+02
1.E+03
1.E+04
1.E+05
1.E+06
1.E+07
Widerstand der Quelle in Ω
08.04.2004
H.Hidber
18