Die Ablenkröhre / Braunsche Röhre

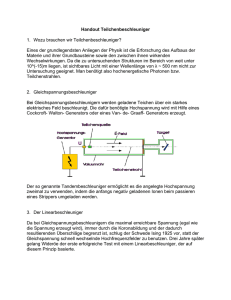
Die Ablenkröhre / Braunsche Röhre
•
•
•
•
•
•
•
Die Ablenkröhre ist eine evakuierte Röhre, in der an der Kathode durch den glühelektrischen Effekt ein Elektronenstrahl erzeugt
wird, der wiederum ein senkrecht zur Bewegungsrichtung verlaufendes E-Feld durchquert und dort „abgelenkt“ wird.
Der Strahl entsteht durch die anliegende Anodenspannung, die die Elektronen in Richtung Anode beschleunigt. Ein Zylinder
verhindert dabei, dass der Strahl zu Beginn schon zerstreut wird.
Passieren die Elektronen die Anode mit einer konstanten Geschwindigkeit vx, so gelangen sie zum Plattenkondensator, zwischen dem
ein E-Feld herrscht.
Durch das elektrische Feld wird der Elektronenstrahl gleichmäßig in y-Richtung
beschleunigt dadurch von seiner geradlinigen Bahn abgelenkt.
Auf Höhe des Kondensators befindet sich ein Koordinatensystem, an dem die
Veränderung des Strahls nachzuvollziehen ist.
Nun können die Ablenkspannungen Uy und die Beschleunigungsspannung UA
beliebig verändert werden um die Auswirkungen am Koordinatensystem
abzulesen. Der Strahl wird während seiner Ablenkung immer eine
parabelförmige Bahn annehmen.
Eine spezielle Form der Ablenkröhre ist die Braunsche Röhre. Bei ihr kann der
Strahl durch einen zweiten Kondensator zusätzlich in z-Richtung beschleunigt
werden.
Wichtige Formeln:
Geschwingikeit der Elektronen in x-Richtung
Gleichförmige Bew. in x-Richtung
Beschleunigung in y-Richtung
Parabelgleichung des Strahls
Beispielaufgaben
Elektronen werden in einer evakuierten Glasröhre durch eine konstante Gleichspannung UA = 285 V in horizontaler Richtung
nach rechts beschleunigt und gelangen dann in das vertikale homogene Feld eines Plattenkondensators mit der Plattenlänge
l = 12 cm und dem Plattenabstand d = 10 cm. An den Platten liegt die konstante Gleichspannung U an. Die obere Platte sei
positiv geladen; die Elektronen treten genau in der Mitte zwischen den Platten in das Feld ein.
a) Berechnen Sie die Geschwindigkeit der Elektronen beim
Eintritt in das Kondensatorfeld.
(Ergebnis 1,00 · 107 m/s)
b) Leiten Sie allgemein die parameterfreie Gleichung der
Bahnkurve bezüglich eines geeigneten
Koordinatensystems her. Begründen Sie, dass die
Bahnkurve Teil einer Parabel ist.
c) Weisen Sie allgemein nach: Verwendet man statt der
Elektronen andere negativ geladene Teilchen, die wie
beschrieben zunächst durch UA beschleunigt und dann mit
U abgelenkt werden, so durchlaufen sie die gleiche
Parabelbahn.