finanzmath_ergeb

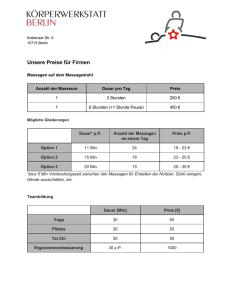
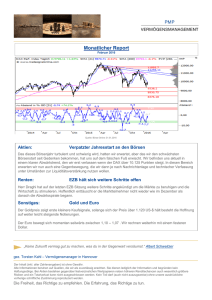
Finanzmathematik
Bewertung von Optionen
Bernhard Kiniger, Christoph Otto, Andreas Reiter,
Daniela Saxenhuber, Christina Stadlmayr, Nora Wiesauer
Optionen



Option: Recht, eine Aktie zu einem
vorher ausgemachten Preis zu kaufen
bzw. zu verkaufen
Eine Option ist ein Recht, keine Pflicht:
Optionskäufer muss nicht ausüben
Optionen bringen Vorteile
 man muss dafür bezahlen
Call-Option
Payoff = ST - K
Ausübungspreis K
Payoff = 0
• S0 Kurswert
• K Ausübungspreis
• T Laufzeit
Up-And-Out-Barrier-Option
300
Barriere B
Ausübungspreis K
Payoff = 0
250
Payoff = ST - K
200
150
Payoff = 0
100
50
25
50
75
100
125
150
175
200
Optionstypen





Call: Recht, eine Aktie zu kaufen
Put: Recht, eine Aktie zu verkaufen
Up-and-out Barriere: Aktienkurs darf die
Barriere nicht überschreiten
Digitale Option
…
Glücksspiel

Würfel:
Auszahlung = Augenzahl

Preis?
 Erwartete Auszahlung:
1
 1  2  3  4  5  6   3.5
6
Ein lehrreiches Beispiel
Call-Option mit K=1
S0 =1
Su=2
Payoff: 1
Sd=1/2
Payoff: 0
Preisfestlegung wie beim Würfelbeispiel
 Preis der Option: 0,67
Ein lehrreiches Beispiel
S0 =1
Su=2
Payoff: 1
Sd=1/2
Payoff: 0
Strategie:
1. Verkaufen Option um 0,6
2. Kaufen Aktien um 0,6
Fall up:
Call kostet 1, Aktien bringen 1,2  Gewinn 0,2
Fall down: Call kostet 0, Aktien bringen 0,3  Gewinn 0,3
No - Arbitrage - Prinzip

Risikoloser, sicherer Gewinn ist
nicht möglich

Der faire Preis einer Option lässt
sich durch dieses Prinzip
bestimmen
No - Arbitrage - Prinzip

Fairer Preis einer Option:
abgezinster, zu erwartender Gewinn bzgl.
der risikoneutralen Wahrscheinlichkeit Q
 rT
p0  e

 EQ [payoff]
Put- und Call-Preis lassen sich durch
einander ausdrücken
Friktionsloser Markt





Keine Spesen
Fixer Zinssatz
Können Aktien jederzeit
kaufen/verkaufen
Einzelhändler beeinflussen Kurs nicht
Short-Selling unbegrenzt möglich
(=Kredit in Aktien)
Aktienkurs-Parameter



Rendite: prozentuelle Entwicklung des
Aktienkurses
Trend oder Drift: Durchschnittliche
Entwicklung einer Aktie
Volatilität: Maß für Kursschwankung
Binomialbaum
up
q
S0
Kurs
#Wege
payoff
S0 u3
1
fuuu
S0 u2 d
3
fuud
S0 u d2
3
fudd
S0 d3
1
fddd
1-q
down
c e
N
0
 rT
 N  N k
k
u N  k d k
     q  (1  q)  f
k 0  k 
N
Geometrisch normalverteilte Irrfahrt

Anhand des historischen Kurses wird ein
möglicher neuer Kurse simuliert
St t  St  e

mt   t 
Im Gegensatz zum Modell des
Binomischen Baumes sind alle Endkurse
möglich
Geometrisch normalverteilte Irrfahrt
300
280
c0  e
 rT
1 N
   payoff( S ( i ) )
N i 1
260
240
220
200
180
80
100
120
140
160
180
200