Ubungen zur Finanzmathematik I - homepages.math.tu

I ̈ M
TU B
Prof. Dr. Peter Friz
Dr. Christian Bayer
Übungen zur Finanzmathematik I
3. Aufgabenblatt vom 30. Oktober 2009
Aufgabe 9. (5 Punkte)
Sei Z ∼ N(0, 1) eine normalverteilte Zufallsvariable und definiere S = eσZ+m , σ > 0, m ∈ R. Man betrachte das
Marktmodell mit Zinssatz r > 0 und einer Aktie mit Preis π1 zum Zeitpunkt 0 und S = S(ω) zum Zeitpunkt 1.
1. Berechnen Sie Erwartungswert und Varianz der Zufallsvariable S.
2. Charakterisieren Sie alle risikoneutralen Maße in diesem Marktmodell.
Bemerkung: die Verteilung von S heißt logarithmische Normalverteilung.
Aufgabe 10. (5 Punkte)
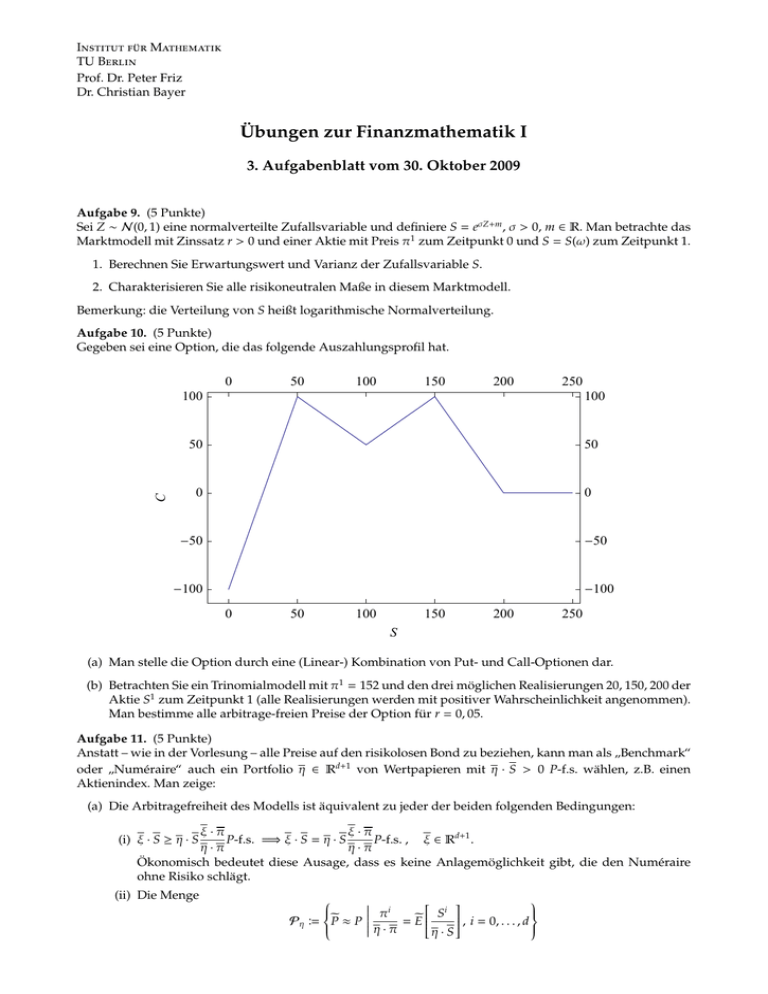
Gegeben sei eine Option, die das folgende Auszahlungsprofil hat.
C
0
50
100
150
200
250
100
100
50
50
0
0
-50
-50
-100
-100
0
50
100
150
200
250
S
(a) Man stelle die Option durch eine (Linear-) Kombination von Put- und Call-Optionen dar.
(b) Betrachten Sie ein Trinomialmodell mit π1 = 152 und den drei möglichen Realisierungen 20, 150, 200 der
Aktie S1 zum Zeitpunkt 1 (alle Realisierungen werden mit positiver Wahrscheinlichkeit angenommen).
Man bestimme alle arbitrage-freien Preise der Option für r = 0, 05.
Aufgabe 11. (5 Punkte)
Anstatt – wie in der Vorlesung – alle Preise auf den risikolosen Bond zu beziehen, kann man als Benchmark“
”
oder Numéraire“ auch ein Portfolio η ∈ Rd+1 von Wertpapieren mit η · S > 0 P-f.s. wählen, z.B. einen
”
Aktienindex. Man zeige:
(a) Die Arbitragefreiheit des Modells ist äquivalent zu jeder der beiden folgenden Bedingungen:
ξ·π
ξ·π
P-f.s. =⇒ ξ · S = η · S
P-f.s. , ξ ∈ Rd+1 .
η·π
η·π
Ökonomisch bedeutet diese Ausage, dass es keine Anlagemöglichkeit gibt, die den Numéraire
ohne Risiko schlägt.
(i) ξ · S ≥ η · S
(ii) Die Menge



e
Pη B 
P≈P







 Si 
πi
 , i = 0, . . . , d 
e 
=E





η·π
η·S
e den
aller äquivalenten risikoneutralen Maße bezüglich des Numéraire η ist nichtleer – wobei E
e
Erwartungswert bezüglich das Wahrscheinlichkeitsmaß P bezeichnet.




e


η·S
dP

e
∗
(b) Pη = 
.
P ≈ P ∃ P ∈ P mit ∗ =


dP
(1 + r)η · π 
(c) Ist η · S nicht P-f.s. konstant, so gilt P ∩ Pη = ∅. Insbesondere gibt es kein universelles Maß, welches
simultan für jedes Numéraire risikoneutral ist.
Hinweis: Es günstig, (a)(ii) und (b) als zusammengehörig zu betrachten.
Aufgabe 12. (5 Punkte)
Man betrachte ein Binomialmodell, also ein Finanzmarktmodell mit Wahrscheinlichkeitsraum Ω = {ω1 , ω2 },
F = 2Ω und pi B P({ωi }) > 0, i = 1, 2, sowie einer Aktie mit Preis π1 zum Zeitpunkt 0 und S1 zum Zeitpunkt 1.
Der Zinssatz sei gegeben durch r > 0, wobei wir annehmen, dass der Markt keine Arbitrage zulässt. Betrachte
nun eine Call-Option mit Strikepreis K.
1. Bestimmen Sie alle äquivalenten Martingalmaße und alle arbitragefreien Preise für die Option.
2. Bestimmen Sie alle replizierenden Strategien für die Option, also alle Portfolios ξ, deren Wert zum
Zeitpunkt 1 mit dem Wert der Option (fast sicher) übereinstimmt. Was ist der Wert der replizierenden
Portfolios zum Zeitpunkt 0?
Abgabe am 5. November 2009 in der Vorlesung.