Übung zur Vorlesung Finanzmathematik (1. Serie)

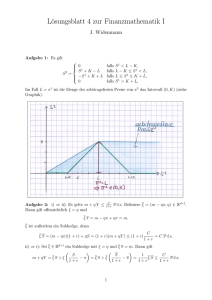
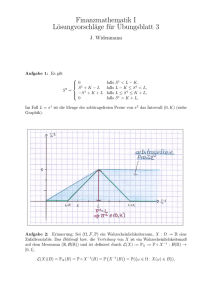
Übung zur Vorlesung
Finanzmathematik
(1. Serie)
1. Es sei (B, S) auf (Ω, F, P) ein Finanzmarktmodell mit T Handelszeitpunkten, wie in der Vorlesung eingeführt. Eine Handelsstrategie (kurz: Strategie)
H heißt dominant, falls sie zulässig und selbstfinanzierend ist und falls eine
weitere zulässige und selbstfinanzierende Stratgie H existiert, so dass
V0 (H) = V0 (H) ,
VT (H) > VT (H) P-f.s.
erfüllt ist. (In diesem Falle sagen wir: H dominiert H.) Man beweise: Es existiert genau dann eine dominante Stratgie, wenn eine zulässige und selbstfinanzierende Strategie H mit
V0 (H) = 0 ,
VT (H) > 0 P-f.s.
existiert.
2. Der Raum Ω sei endlich. Man zeige: Es existiert genau dann eine dominante
e mit
Strategie H, wenn eine zulässige und selbstfinanzierende Strategie H
e < 0,
V0 (H)
e ≥ 0 P-f.s.
VT (H)
exisiert.
Hinweis: Man verwende (wo zweckmäßig) diskontierte Werteprozesse.
3. Es sei C = VT (H) der Wert eines Portfolios (Auszahlung) zum Zeitpunkt
T . Wie groß ist der „arbitragefreie“ Preis von C im Zeitpunkt t = 0, vorausgesetzt, es gibt einen solchen Preis? (Arbitragefrei heißt, dass weder Käufer
noch Verkäufer mit dem Preis einen risikolosen Gewinn erzielen können.)
4. Man sagt, dass das Finanzmarktmodell dem Gesetz der Eindeutigkeit des
Preises genügt, wenn für beliebige zulässige und selbstfinanzierende Strategien H und H mit
VT (H) = VT (H) P-f.s.
stets
V0 (H) = V0 (H) P-f.s.
erfüllt ist. Man beweise, dass das Gesetz der Eindeutigkeit des Preises gilt,
falls für das Finanzmarktmodell keine dominanten Strategien existieren.
Abgabe: Freitag, 27. April 2007 zur Übungszeit
1