Finanzmathematik I Lösungvorschläge für¨Ubungsblatt 1

Finanzmathematik I
Lösungvorschläge für Übungsblatt 1
J. Widenmann
Aufgabe 1: Zu zeigen ist, dass Q die Definition Ü.1.1.2 erfüllt. Zunächst bemerken wir,
dass Q wegen der Annahme f ≥ 0 Werte in R+ annimmt. Außerdem gilt:
R
R
(i) Q(∅) = ∅ f (ω)P(dω) = 1∅ (ω)f (ω)P(dω) = 0.
(ii) Sei (Ai )i≥1 eine Folge paarweise disjunkter Mengen in F, dann gilt
! Z
Z
[
Q
Ai = S
f (ω)P(dω) = 1Si≥1 Ai (ω)f (ω)P(dω)
i≥1
i≥1
=
Ai
Z X
1Ai (ω)f (ω)P(dω)
i≥1
monotone
=
Konvergenz
X
Q(Ai ).
i≥1
Foglich ist Q ein Maß.
Aufgabe 2: Da Q P wissen wir, dass
dQ
dP
≥ 0 existiert.
“⇒” Sei nun auch P Q. Es gilt für A ∈ F
Z
Z
dQ
dQ
Q(A) =
dP =
dP =
dP
dP
A
>0}
A∩{ dQ
dP
Z
>0}
{ dQ
dP
dQ
1A
dP =
dP
Z
1A dQ
>0}
{ dQ
dP
Insbesondere gilt für A = Ω, dass Q( dQ
> 0) = 1 und wegen der Annahme P Q
dP
natürlich auch P( dQ
>
0)
=
1.
dP
−1
“⇐” Ist dQ
> 0 P-f.s., betrachten wir dQ
. Dann gilt für A ∈ F
dP
dP
−1
Z −1
Z
Z
dQ dQ
dQ
P(A) =
dP =
dP =
dQ
dP
dP
A
A
A dP
−1
Folglich besitzt P die Dichte dQ
bzgl. Q. Also gilt auch P Q.
dP
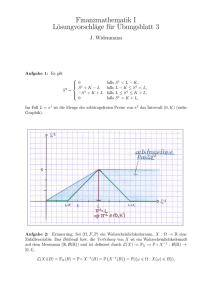
Aufgabe 3:
i) Nach Konstruktion von F gilt: es gibt genau eine Menge A ∈ F mit P(A) = 0,
nämlich die leere Menge A = ∅. Wegen Q Wahrscheinlichkeitsmaß, gilt offensichtlich Q(∅) = 0, also folgt Q P. Nach dem Satz von Radon-Nikodym existiert also
in diesem Wahrscheinlichkeitsraum IMMER eine Dichte dQ
, mit dQ
∈ L1 (Ω, F, P)
dP
dP
dQ
und dP ≥ 0 P-f.s.
)
ii) Jede Zufallsvariable auf diesem Wahrscheinlichkeitsraum
(also auch die Dichte dQ
dP
Pn
ist
von
der
Form
X
:
Ω
→
R,
X
=
c
1
,
c
∈
R.
Sei
nun
zunächst
Ω
=
i=1 i Ai i
Sn
A
.
Der
Satz
von
Radon-Nikodym
ergibt
i
i=1
dQ
∀A ∈ F : Q(A) = EP
1A .
dP
Wir setzen ein:
"
Q(Aj ) = EP
n
X
#
ci 1Ai 1Aj = EP cj 1Aj = cj P(Aj ).
i=1
Also haben wir cj =
Q(Aj )
,
P(Aj )
und damit
n
dQ X Q(Ai )
=
1Ai .
dP
P(A
)
i
i=1
Sn
Sn
Im Falle Ω 6= i=1 Ai definieren wir AC
Ai .
n+1 :=
i=1 Pn+1
Ist P(An+1 ) > 0, so gilt dann analog Q(An+1 ) = EP
i=1 ci 1Ai 1An+1 = cn+1 P(An+1 )
Pn+1 Q(Ai )
=
und damit dQ
i=1 P(Ai ) 1Ai .
dP
n
P
Q(Ai )
Ist hingegen P(An+1 ) = 0, so gilt erneut dQ
=
1 , denn z.B. für Ω (=
dP
P(Ai ) Ai
i=1
n+1
S
Aj ):
j=1

Q(Ω) = EP 
n
X
Q(Ai )
i=1
= Q(
n
[
i=1
P(Ai )

1Ai 1n+1
S
Aj
=
j=1
n
X
Q(Ai )
i=1
P(Ai )
P(Ai )
Ai ) = Q(Ω) − Q(An+1 ) = 1
| {z }
=0,da Q≈P
Aufgabe 4:
(i) Da EP [X|G] G-messbar ist, gilt {EP [X|G] ≥ 0} ∈ G sowie {EP [X|G] < 0} ∈ G und
insbesondere
EP EP [X|G]+ = EP [EP [X|G] , EP [X|G] ≥ 0]
= EP [X, EP [X|G] ≥ 0] ≤ EP [|X|] < ∞
Analog zeigt man EP EP [X|G]− < ∞, also EP [X|G] ∈ L1 (Ω, G, P).
(ii) Ist X ≥ 0, dann gilt
0 ≤ EP EP [X|G]− = −EP [EP [X|G] , EP [X|G] < 0]
| {z }
≥0
= − EP [X, EP [X|G] < 0] ≤ 0,
|
{z
}
≥0,daX≥0
also EP EP [X|G]− = 0. Folglich gilt EP [X|G]− = 0 P-f.s., d.h. EP [X|G] ≥ 0
P-f.s..
(iii) Folgt direkt aus der Definition.
(iv)
– EP [X] ist als Konstante {∅, Ω}-messbar.
– Für A = ∅ gilt
EP [EP [X] , ∅] = 0 = EP [EP [X|G] , ∅]
– Für B = Ω gilt
Def
EP [EP [X] , Ω] = EP [X, |{z}
Ω ] = EP [EP [X|G] , Ω]
∈G
Es folgt die Behauptung.
(v) Es gilt EP [EP [X|G]] = EP [EP [X|G] , Ω] = EP [X, Ω] = EP [X]
(vi) (1)
- EP [X|A] ist nach Definition A-messbar.
- Sei A ∈ A, dann gilt
A∈A⊂G
EP [EP [X|A] , A] =EP [X, A] = EP [EP [X|G] , A]
=EP [EP [EP [X|G] |A] , A]
(2)
- EP [X|A] ist nach Definition A-, also auch G-messbar.
- Sei A ∈ G, dann gilt
EP [EP [X|A] , A] = EP [EP [EP [X|A] |G] , A]
Es folgt die Behauptung.
(vii) Seien X, Y ∈ L1 (Ω, F, P), sowie α, β ∈ R, dann ist zu zeigen: EP [αX + βY |G] =
αEP [X|G] + βEP [Y |G]. Es gilt aber
– αEP [X|G]+βEP [Y |G] ist als linearkombination G-messbarer Funktionen selbst
G-messbar.
– Sei A ∈ G, dann gilt
EP [αEP [X|G] + βEP [Y |G] , A] = αEP [EP [X|G] , A] + βEP [EP [Y |G] , A]
= EP [αX, A] + EP [βY, A] = EP [αX + βY, A]
(viii) Folgt direkt aus (ii) und (vii)
(ix) Wir zeigen hier nur den vereinfachten Fall, in dem Z zusätzlich beschränkt ist. Die
Behauptung gilt aber auch ganz allgemein. Dies dürfen Sie o.B.d.A für alle weiteren
Übungsaufgaben verwenden.
Für den hier gezeigten Beweis verwenden wir das Konzept der maßtheoretischen
Induktion
– ZEP [X|G] ist G-messbar.
– Sei A ∈ G und Z =
Pn
k=1
αk 1Bk für αk ∈ R, Bk ∈ G, n ∈ N. Dann gilt
n
X
EP [ZEP [X|G] , A] =
k=1
αk EP [EP [X|G] , A ∩ Bk ] =
| {z }
n
X
∈G
αk EP [X, A ∩ Bk ]
k=1
= EP [ZX, A] = EP [EP [ZX|G], A]
Für den allgemeinen Fall verwenden wir, dass jede beschränkte G-messbare
Funktion Z durch eine Folge (Zn )n∈N von Funktionen der obigen Gestalt approximiert werden kann. Dann folgt
EP [ZEP [X|G] , A]
dom. Konvergenz (!)
=
dom. Konvergenz (!)
=
(x)
lim EP [Zn EP [X|G] , A] = lim EP [Zn X, A]
n→∞
n→∞
EP [ZX, A] = EP [EP [ZX|G], A]
– EP [X] ist als Konstante trivialerweise G-messbar.
– Sei A ∈ G, dann gilt
EP [EP [X] , A] = EP [X] EP [1A ]
X unabh. von G
=
EP [X, A] = EP [EP [X|G] , A]
(xi) Zunächst bemerken wir, dass für eine konvexe Funktion f die Abbildung z 7→
f (z)−f (y)
monoton steigend ist. Insbesondere existieren für alle y ∈ R die links- und
z−y
(y)
(y)
rechtsseitigen Ableitungen fl0 (y) = limz%y f (z)−f
, fr0 (y) = limz&y f (z)−f
und es
z−y
z−y
gilt für alle y1 < y < y2 ∈ R:
(y)
f (y1 )−f (y)
≤ fl0 (y) ≤ fr0 (y) ≤ fl0 (y) = f (yy22)−f
und daher für alle x ∈ R:
y1 −y
−y
f (x) ≥ f (y) + (x − y)fr0 (y).
(*)
Nun zum eigentlichen Beweis. Zunächst bemerken wir, dass f stetig, also B(R)messbar ist. Außerdem ist x 7→ fr0 (x) = limn→∞ n(f (x+ n1 −f (x)) als Limes messbar.
Nun setzen wir X und Y := EP [X|G] in (*) ein und erhalten
f (X) ≥ f (Y ) + (X − Y )fr0 (Y ) und daher mit (viii):
EP [f (X)|G] ≥ EP [ f (Y ) |G] + EP [X|G] fr0 (Y ) − Y fr0 (Y ) = f (EP [X|G])
| {z }
| {z } | {z }
G−m.b.
G-m.b.
G−m.b.
(xii) Zunächst bemerken wir, dass wegen (viii) auch EP [Xn |G] P-f.s. monoton steigend,
also konvergent gegen eine ZVe Z konvergiert.
– Z ist als Limes G-messbarer ZVen ebenfalls G-messbar.
– Wegen 0 ≤ EP [Xn |G] ≤ EP [X|G] ist Z ∈ L1 (Ω, F, P).
Sei nun A ∈ G, dann gilt
EP [Z, A] = lim EP [EP [Xn |G], A] = lim EP [Xn , A] = EP [X, A]
n→∞
n→∞
(xiii) Zunächst bemerken wir, dass X ∈ L1 (Ω, F, P), da auch |X| ≤ Z P-f.s. Wir setzen
Un := inf m≥n Xm und Vn = supm≥n Xm , dann gilt
−Z ≤ Un ≤ Xn ≤ Vn ≤ Z
und außerdem Un % X sowie Vn & X P-f.s..
Mit (xii) gilt dann
EP [Un |G] → EP [X|G] sowie EP [Vn |G] → EP [X|G]
Aus (viii) folgt insbesondere EP [Un |G] ≤ EP [Xn |G] ≤ EP [Vn |G] und somit mit dem
gezeigten die Behauptung.
Aufgabe 5: Sei A ∈ G. Wegen Q P auf F gilt offensichtlich auch Q P auf G ⊂ F.
Dann gilt
dQ P dQ =E
G ,
dP G
dP
denn:
P
Q(A) = E
dQ
P
P dQ 1A = E E
G 1A .
dP
dP
Wegen
Z
dQ P dQ Q
E
=
E
G = 0
G dP = 0
dP
dP
|G ]=0}
{EP [ dQ
dP
| G > 0 = 1.
folgt Q EP dQ
dP
Sei X ≥ 0, A ∈ G. Dann gilt
dQ
dQ Q
P
P
P
E [X · 1A ] = E X ·
· 1A = E E X ·
G · 1A
dP
dP
#
" E P dQ | G dQ
dP
· 1{E P [ dQ |G ]>0} · 1A
= EP EP X ·
G · P dQ
dP
dP
E dP | G
dQ + EP EP X ·
G · 1{E P [ dQ |G ]=0} · 1A
dP
dP
#
" dQ
E P X · dP | G
(∗)
· 1A + 0.
= EQ
E P dQ
|G
dP
P
Damit ist die Behauptung gezeigt für X ≥ 0. Für X ∈ L1 (Ω, F, Q) zerlege X = X + − X −
in Positiv- und Negativteil und benutze die Linearität der bedingten Erwartung.
Zu (∗): Wegen
P dQ
P
P dQ
E
· 1{E P [ dQ |G ]=0} = E E
· 1{E P [ dQ |G ]=0} G
dP
dP
dP
dP
P
P dQ =E E
G · 1{E P [ dQ |G ]=0} = 0
dP
dP
und
dQ
dP
≥ 0 P-f.s. folgt
dQ
· 1 P dQ
= 0 P-f.s.
dP {E [ dP |G ]=0}
Also haben wir
E
P
E
P
dQ X·
G · 1{E P [ dQ |G ]=0} · 1A
dP
dP



 





dQ

P P
· 1{E P [ dQ |G ]=0} G  ·1A 
= E E X ·
 = 0.


}
| dP {z dP


=0 P-f.s.
|
{z
}
=0 P-f.s.
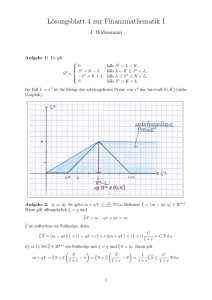
Aufgabe 6:
(i) ⇔ (ii) ist klar, da wir die einzelnen Ungleichungen der beiden Definitionen nur mit den
1
(deterministischen) Konstanten (1 + r) bzw. 1+r
multiplizieren müssen.
(i) ⇒ (iii) Sei η eine Arbitragemöglichkeit, dann gilt insbesondere 0 ≥ η̄ · π̄ = η 0 +η ·π. Folglich
gilt
η · S − (1 + r)η · π ≥ η · S + (1 + r)η 0 = η̄ · S̄.
Da nach Voraussetzung η̄ · S̄ P-f.s. nicht-negativ und außerdem strikt positiv mit
positiver Wahrscheinlichkeit ist, muss dies auch für η · S − (1 + r)η · π gelten. (Es
gilt also ξ = η.)
(iii) ⇒ (i) Sei ξ gegeben wie in (iii), dann betrachten wir das Portfolio η̄ = (η 0 , ξ), mit η 0 :=
−ξ · π. Dann gilt offensichtlich η̄ · π̄ = 0 und außerdem
η̄ · S̄ = −(1 + r)ξ · π + ξ · S,
was nach Voraussetzung P-f.s. nicht negativ und positiv mit positiver Wahrscheinlichkeit ist. η̄ ist also eine Arbitragestrategie.