Finanzmathematik I Lösungvorschläge für¨Ubungsblatt 3

Finanzmathematik I
Lösungvorschläge für Übungsblatt 3
J. Widenmann
Aufgabe 1: Es gilt

0


 1
S +K −L
S2 =
−S 1 + K + L



0
falls
falls
falls
falls
S 1 < L − K,
L − K ≤ S 1 < L,
L ≤ S 1 ≤ K + L,
S 1 > K + L,
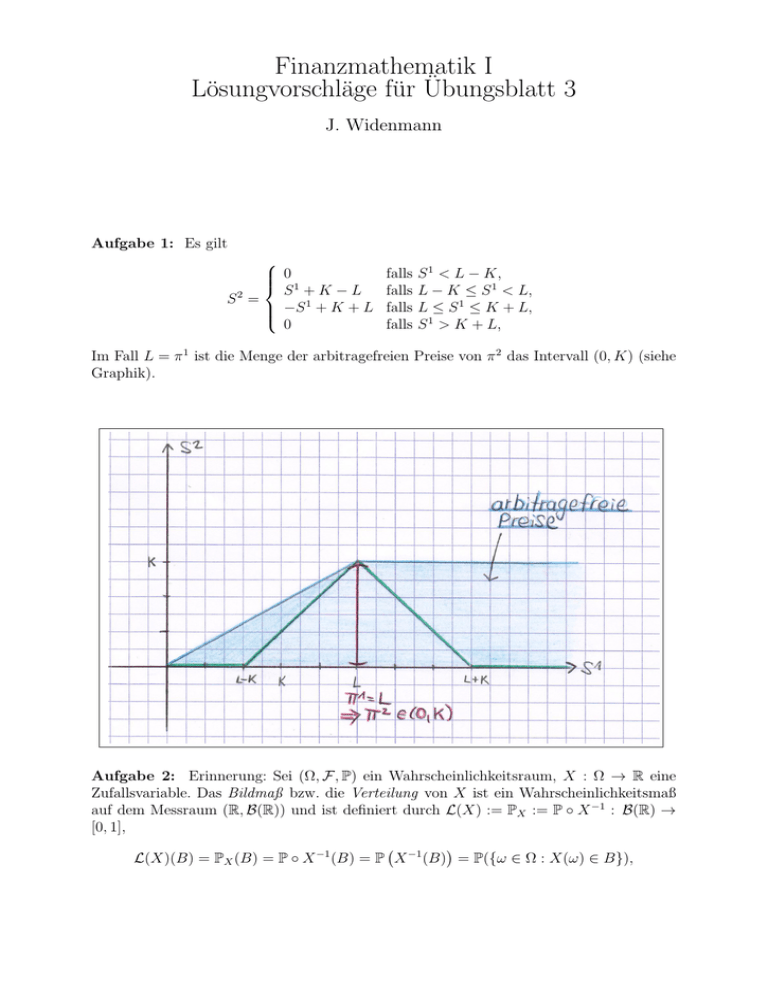
Im Fall L = π 1 ist die Menge der arbitragefreien Preise von π 2 das Intervall (0, K) (siehe
Graphik).
Aufgabe 2: Erinnerung: Sei (Ω, F, P) ein Wahrscheinlichkeitsraum, X : Ω → R eine
Zufallsvariable. Das Bildmaß bzw. die Verteilung von X ist ein Wahrscheinlichkeitsmaß
auf dem Messraum (R, B(R)) und ist definiert durch L(X) := PX := P ◦ X −1 : B(R) →
[0, 1],
L(X)(B) = PX (B) = P ◦ X −1 (B) = P X −1 (B) = P({ω ∈ Ω : X(ω) ∈ B}),
für B ∈ B(R). Wir können auch besondere Verteilungen auf dem Messraum (Ω, F)
definieren, z. B. die Einpunktverteilung bzw. das Dirac-Maß. Für ω0 ∈ Ω gilt dabei
δω0 : F → [0, 1],
1 falls ω0 ∈ A,
δω0 (A) =
0 falls ω0 ∈
/ A.
Man kann leicht zeigen, dass das ein Wahrscheinlichkeitsmaß ist. Das kann man natürlich
auch auf (R, B(R)) definieren, so wie in dieser Aufgabe:
a)
δ0 (B) =
1 falls 0 ∈ B,
0 falls 0 ∈
/ B,
analog gilt δ2 (B) =
1 falls 2 ∈ B,
0 falls 2 ∈
/ B,
für B ∈ B(R). Dann gilt natürlich für die Zufallsvariable S 1 : Ω → R mit L(S 1 )(B) =
PS 1 (B) = P ◦ (S 1 )−1 = 21 (δ0 + δ2 )(B) :
1
1
1
(δ0 + δ2 )({0}) = (1 + 0) =
2
2
2
und
1
1
1
(δ0 + δ2 )({2}) = (0 + 1) = ,
2
2
2
d.h. S 1 nimmt nur die zwei Werte 0 und 2 mit positiver Wahrscheinlichkeit an. Also
haben wir
0 mit P(S 1 = 0) = 1/2,
1
S =
2 mit P(S 1 = 2) = 1/2,
analog
2
S =
0 mit P(S 2 = 0) = 1/2,
2 mit P(S 2 = 2) = 1/2,
wobei S 1 , S 2 unabhängig. Weiterhin ist dann offensichtlich
0 mit P(S 3 = 0) = 1/2,
3
S =
1 mit P(S 3 = 1) = 1/2,
und schließlich

0



0
S4 =
0



2
mit
mit
mit
mit
P(S 1
P(S 1
P(S 1
P(S 1
= 0, S 2
= 2, S 2
= 0, S 2
= 2, S 2
= 0) = 1/4,
= 0) = 1/4,
0 mit P(S 4 = 0) = 3/4,
=
= 2) = 1/4,
2 mit P(S 4 = 2) = 1/4.
= 2) = 1/4,
Der gegebene Markt ist unter der Annahme F = σ(S 1 , ..., S 4 ) redundant, da S 3 =
1 1
S P-f.s. ist. Insbesondere ist wegen π 1 = 1 für jedes äquivalente Martingalmaß
2
P∗ ∈ P der arbitragefreie Preis π 3 eindeutig gegeben durch π 3 = 12 . Außerdem
genügt es, sich bei der Suche nach arbitragefreien Preisen auf die durch S 1 , S 2 , S 4
gegebenen Restriktionen zu beschränken. Die Zeichnung auf der nächsten Seite zeigt
dann, dass π 4 ∈ (0, 1) liegen muss. Also gilt M = {(1/2, y) | y ∈ (0, 1)}.
b) Ein äquivalentes Martingalmaß P∗ zu (1/2, π 4 ) ist durch folgende Bedingungen gegeben: sei dazu p∗1 := P∗ [S 1 = 0, S 2 = 0], p∗2 := P∗ [S 1 = 0, S 2 = 2], p∗3 := P∗ [S 1 =
2, S 2 = 0], p∗4 := P∗ [S 1 = 2, S 2 = 2]:
p∗1 , p∗2 , p∗3 , p∗4 > 0 und p∗1 + p∗2 + p∗3 + p∗4 = 1,
1 = E∗ [S 1 ] = 2(p∗3 + p∗4 ),
1 = E∗ [S 2 ] = 2(p∗2 + p∗4 ),
1/2 = E∗ [S 3 ] = (p∗3 + p∗4 ),
π4
=
E∗ [S 4 ] = 2p∗4
⇔
p∗4 =
π4
.
2
Es folgen p∗2 = p∗3 = (1 − π 4 )/2 und p∗1 = p∗4 = π 4 /2.
Aufgabe 3:
a) Ein ausreichender und besonders einfacher Wahrscheinlichkeitsraum ist Ω = {ω− , ω+ }
mit F = P(Ω). Setzen wir S 1 (ω+ ) = 8 und S 1 (ω− ) = 2, dann muss für das Wahrscheinlichkeitsmaß P die Bedingung P({ω+ }) = 23 und P({ω− }) = 13 gelten.
b) Zunächst suchen wir (aufgrund des FTAP) ein zu P äquivalentes Martingalmaß P∗ .
Wegen der Forderung nach Äquivalenz muss P∗ S 1 = p∗ δ8 + (1 − p∗ )δ2 mit p∗ > 0
gelten. Die Martingalmaß-Bedingung verlangt
1 S
4 · 8p∗ 4 · 2(1 − p∗ )
1
EP∗
− π1 =
+
− 4 = 0 ⇔ p∗ =
1+r
5
5
2
Man erkennt sofort, dass das äquivalente Martingalmaß eindeutig ist.
Der eindeutige arbitrage-freie Preis π C von C = (S − 5)+ ist daher
1
(S − 5)+
4
C
π = EP ∗
=
(8 − 5) = 1.2 .
1 + 1/4
5·2
1
c) Die Strategie ξ¯ = (π C − π C , 0, −1, 1) ist eine Arbitragestrategie und daher der
Markt nicht arbitrage-frei.
Aufgabe 4: Wir zeigen zunächst, dass
sup M = inf Π(C) ,
wobei M := m ∈ [0, ∞) | ∃ ξ ∈ Rd : m + ξY ≤
C
1+r
P − f.s. .
“ ≤ ” Zunächst bemerken wir, dass M 6= ∅, da z.B 0 ∈ M mit der trivialen Strategie. Sei
C
P-f.s.. Dann folgt für alle P∗ ∈ P,
also x ∈ M und ξ ∈ Rd derart, dass x + ξY ≤ 1+r
dass
C
EP∗ [
] ≥ EP∗ [x + ξY ] = x .
1+r
Damit haben wir sup M ≤ inf Π(C) gezeigt.
“ ≥ ” Sei nun m ∈ R mit m < inf Π(C) beliebig. Dann gibt es nach dem FTAP eine
Arbitragemöglichkeit (ν, ν d+1 ) ∈ Rd × R im erweiterten Markt (S 0 , S 1 , . . . , S d , C),
C
C
− m) ≥ 0 P-f.s und P(νY + ν d+1 ( 1+r
− m) > 0) > 0. Da der
d.h. νY + ν d+1 ( 1+r
d+1
ursprüngliche Markt arbitragefrei ist, muss ν
6= 0 gelten. Für alle P∗ ∈ P folgt
weiterhin, dass
EP∗ [νY + ν d+1 (
C
C
− m)] = ν d+1 EP∗ [(
− m] ≥ 0
1+r
1+r
und deshalb ν d+1 > 0. Sei ξ := −ν/ν d+1 , dann ist m + ξY ≤
Da m beliebig gewählt war, muss sup M ≥ inf Π(C) gelten.
C
1+r
P-f.s., also m ∈ M .
C
Damit haben wir sup M = inf Π( 1+r
) gezeigt. Nun wollen wir zeigen, dass das Supremum
von M tatsächlich angenommen wird, also ein Maximum ist.
O.B.d.A. können wir annehmen, dass (S11 , . . . , S1d ) linear unabhängig sind, d.h. aus ξ ∈
Rd : ξS1 = 0 P-f.s. folgt ξ = 0. Sei (xn )n∈N ⊂ M eine Folge, die gegen sup M konvergiert
C
und seien ξn ∈ Rd Strategien, so dass xn +ξn Y ≤ 1+r
P-f.s.. Falls eine konvergente Teilfolge
d
(ξnk )k∈N mit Grenzwert ξ ∈ R existiert, dann gilt offensichtlich
sup M + ξY ≤
C
1+r
P − f.s.
und somit sup M ∈ M ⇔ sup M = max M .
Angenommen alle Teilfolgen divergieren, dann wähle für k ∈ N ξnk derart, dass kξnk k > k
für irgendeine Norm k.k auf Rd . Dann sind ηk := −ξnk /kξnk k Elemente der entsprechenden
Einheitskugel. Aus der Kompaktheit dieser Kugel folgt, dass wir, eventuell unter Übergang
zu einer Teilfolge, annehmen können, dass die Folge ηk gegen ein η ∈ Rd mit kηk = 1
konvergiert. Dann folgt aber aus
− sup M
C
+ ηk Y ≥
kξnk k
(1 + r)kξnk k
P − f.s.
für k → ∞, dass ηY ≥ 0 P-f.s.. Aus der Arbitragefreiheit des ursprünglichen Marktes
schließen wir nun zuerst, dass ηY = 0 P-f.s. und aufgrund der linearen Unabhängigkeit,
dass η = 0. Dies ist aber ein Widerspruch zu kηk = 1. Also muss (ξn )n∈N eine konvergente
Teilfolge enthalten.