Lösungsblatt 4 zur Finanzmathematik I

Lösungsblatt 4 zur Finanzmathematik I
J. Widenmann
Aufgabe 1: Es gilt

0


 1
S
+K −L
S2 =
−S 1 + K + L



0
falls
falls
falls
falls
S 1 < L − K,
L − K ≤ S 1 < L,
L ≤ S 1 ≤ K + L,
S 1 > K + L,
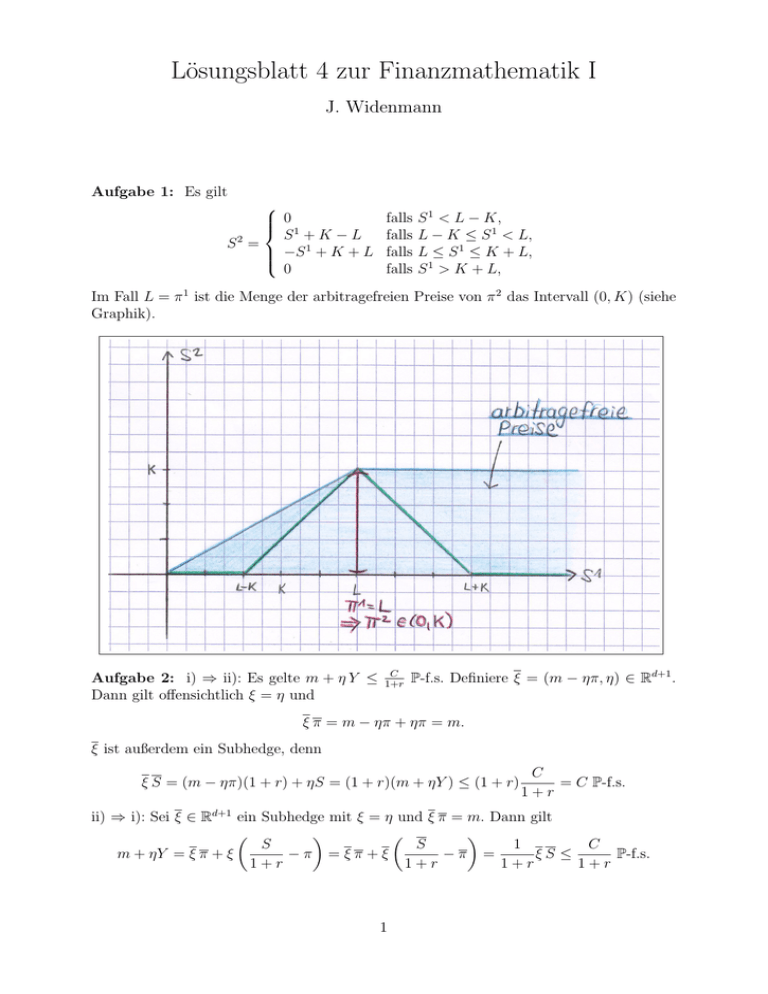
Im Fall L = π 1 ist die Menge der arbitragefreien Preise von π 2 das Intervall (0, K) (siehe
Graphik).
Aufgabe 2: i) ⇒ ii): Es gelte m + η Y ≤
Dann gilt offensichtlich ξ = η und
C
1+r
P-f.s. Definiere ξ = (m − ηπ, η) ∈ Rd+1 .
ξ π = m − ηπ + ηπ = m.
ξ ist außerdem ein Subhedge, denn
ξ S = (m − ηπ)(1 + r) + ηS = (1 + r)(m + ηY ) ≤ (1 + r)
C
= C P-f.s.
1+r
ii) ⇒ i): Sei ξ ∈ Rd+1 ein Subhedge mit ξ = η und ξ π = m. Dann gilt
S
S
1
C
m + ηY = ξ π + ξ
ξS ≤
−π =ξπ+ξ
−π =
P-f.s.
1+r
1+r
1+r
1+r
1
Aufgabe 3: Erinnerung: A ∈ F heißt Atom auf (Ω, F, P), falls P(A) > 0 und ∀B ∈ F
mit B ⊆ A gilt P(B) = 0 oder P(B) = P(A).
S
≥: Sei A1 , . . . , An irgendeine Partition von Ω (d.h. ni=1 Ai = Ω, P(Ai ∩ Aj ) = ∅ ∀i 6= j)
mit Ai ∈ F und P(Ai ) > 0 ∀i. Die dazugehörigen Indikatorfunktionen 1A1 , . . . , 1An sind
linear unabhängige Vektoren im Vektorraum der messbaren Zufallsvariablen
L0 (Ω, F, P),
P
n
denn die Null 0 ∈ L0 (Ω, F, P) lässt sich nur erzeugen als 0 = i=1 αi 1Ai (αi 6= 0) falls
1Ai (ω) = 0 ∀i. Dann gilt offensichtlich dim L0 (Ω, F, P) ≥ n. Damit ist die Behauptung
gleichzeitig für n = ∞ gezeigt.
≤: Umgekehrt sei n0 < ∞, n0 = sup{n ∈ N | ∃ A1 , . . . , An Zerlegung von Ω mit Ai ∈
F, P(Ai ) > 0} mit der dazugehörigen Partition A1 , . . . , An0 von Ω. Dann ist jedes Ai ein
Atom, denn sonst wäre n0 nicht maximal. Also ist jede Zufallsvariable Z ∈ L0 (Ω, F, P)
P-f.s. konstant auf Ai , d.h. Z hat die Form
Z=
n0
X
zi 1Ai P-f.s.,
i=1
mit zi ∈ R. Also stellen die Indikatorfunktionen 1A1 , . . . , 1An0 eine Basis von L0 (Ω, F, P)
dar, d.h. dim L0 (Ω, F, P) = n0 .
Aufgabe 4: In diesem Finanzmarkt gilt nicht, dass jedes Derivat replizierbar ist. Beweis durch Widerspruch: angenommen, alle Derivate seien replizierbar. Wir betrachten
den eingeschränkten Raum L0 (Ω, σ(S 0 , S 1 , S 2 ), P). In diesem Raum ist jeder Claim ein
Derivat. In der Vorlesung (Beweis Lemma 1.15) haben wir gezeigt, dass falls alle Claims
replizierbar sind (und das ist ja gerade in dieser Aufgabe der Fall) gilt
dim L0 (Ω, σ(S 0 , S 1 , S 2 ), P) ≤ d + 1 = 3.
Analog zu Aufgabe 2, Blatt 3 nehmen S 1 , S 2 nur die Werte 1, . . . , n an jeweils mit Wahrscheinlichkeit 1/n, d.h. wegen der Unabhängigkeit ist die Verteilung von S = (S 1 , S 2 ) ein
Gitter auf R2 mit n2 Massepunkten. σ(S 0 , S 1 , S 2 ) besteht also aus n2 Atomen. Wegen
Aufgabe 2 gilt außerdem
n2 = dim L0 (Ω, σ(S 0 , S 1 , S 2 ), P),
also haben wir
n2 = dim L0 (Ω, σ(S 0 , S 1 , S 2 ), P) ≤ d + 1 = 3,
das ist aber ein Widerspruch für n > 1.
Wir können alternativ ein Beispiel für ein Derivat geben, welches explizit nicht replizierbar
ist, z. B. C = 1{S 1 =S 2 =1} . Zu diesem Derivat können wir kein ξ ∈ R3 finden, so dass
C = ξ S P-f.s. So ein ξ müsste für n > 1 mindestens die Gleichungen


 
1+r 1 1
1
1 + r 1 2
0


 
1 + r 2 1 ξ = 0 .
1+r 2 2
0
2
erfüllen. Dieses Gleichungssystem ist aber offensichtlich nicht lösbar.
Aufgabe 5: Sei (Ω, F, P) ein Wahrscheinlichkeitsraum, G ⊆ F eine Unter-σ-Algebra von
F und X eine Zufallsvariable auf (Ω, F, P). Y = E[X | G] ist definiert durch
1) Y ∈ L1 (Ω, G, P),
2) E[Y 1A ] = E[X 1A ] ∀A ∈ G.
Hier: G = σ({ω1 , ω2 }) = {Ω, ∅, {ω1 , ω2 }, {ω3 , ω4 }}. Wegen 1) hat Y die
P4 Form Y =
y1 1{ω1 ,ω2 } +y2 1{ω3 ,ω4 } , y1 , y2 ∈ R (siehe auch Aufgabe 1, Blatt 2). X(ω) = i=1 i 1{ωi } (ω),
= 10
. Wegen 2) fordern wir ∀A ∈ G
E[X] = 1+2+3+4
4
4
E[(y1 1{ω1 ,ω2 } + y2 1{ω3 ,ω4 } ) 1A ] = E[X 1A ].
Für A = {ω1 , ω2 } haben wir
E[y1 1{ω1 ,ω2 } ] = E[X 1{ω1 ,ω2 } ]
⇔
3
y1 = ,
2
⇔
7
y2 = .
2
für A = {ω3 , ω4 } erhalten wir
E[y2 1{ω3 ,ω4 } ] = E[X 1{ω3 ,ω4 } ]
Dann gilt offensichtlich 2) auch für A = Ω:
E[Y ] =
y1 y2
10
+
=
= E[X].
2
2
4
Also Y = E[X | G] = 23 1{ω1 ,ω2 } + 72 1{ω3 ,ω4 } .
3