Widerstandsnetzwerke

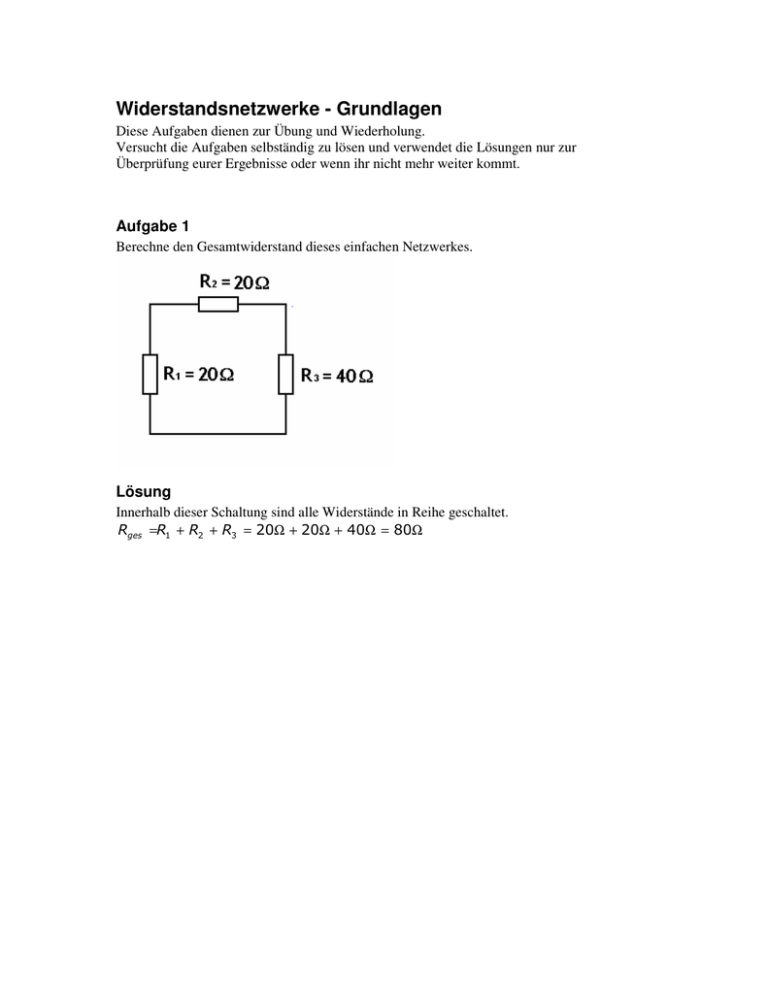
Widerstandsnetzwerke - Grundlagen
Diese Aufgaben dienen zur Übung und Wiederholung.
Versucht die Aufgaben selbständig zu lösen und verwendet die Lösungen nur zur
Überprüfung eurer Ergebnisse oder wenn ihr nicht mehr weiter kommt.
Aufgabe 1
Berechne den Gesamtwiderstand dieses einfachen Netzwerkes.
Lösung
Innerhalb dieser Schaltung sind alle Widerstände in Reihe geschaltet.
Rges =R1 + R2 + R3 = 20Ω + 20Ω + 40Ω = 80Ω
Aufgabe 2
Das Netzwerk aus Aufgabe 1 kann in eine andere Schaltung eingebaut werden. Es soll an den
Punkten A und B angeschlossen werden. Berechne den Innenwiderstand des Netzwerks der
zwischen den Punkten A und B wirkt.
Hinweis
Der Gesamtwiderstand ist nicht gleich dem Ergebnis aus Aufgabe 1. Der Grund ist, dass
zwischen den Punkten A und B die Widerstände R1 und R2 parallel zu R3 geschaltet sind.
Lösung
R12 =R1 + R2 =20Ω + 20Ω = 40Ω
Rges =
R12 * R3
40Ω * 40Ω 1600Ω 2
=
=
= 20Ω
R12 + R3
40Ω + 40Ω
80Ω
Aufgabe 3
In diesem Gleichspannungsnetzwerk sollen die Pfeilrichtungen aller Spannungsabfälle und
Ströme (auch die Maschenrichtungen) eingetragen und anschließend berechnet werden.
Hinweise
Spannungspfeile und zeigen immer vom positiven zum negativeren Potential. Der Strom
fließt in Richtung der Spannung (technische Stromrichtung von + nach -)
Zum berechnen der Ströme und Spannungen geht man immer nach dem gleichen Prinzip vor:
Man sucht sich eine Größe, zu deren Berechnung alle anderen Größen bekannt sind. Nach
jedem Schritt lässt sich eine andere Größe finden, zu deren Berechnung nun alle anderen
Größen bekannt sind.
Werkzeuge:
Ohmsches Gesetzt:
Maschenregel:
Knotenregel:
Lösung
U=R*I
0 = - Uq1 + UR1 + UR2
Die Summe aller Spannungsabfälle einer Masche ist 0
I = I1 + I2
Die Summe aller eingehenden und ausgehenden Ströme eines
Knotenpunktes ist 0
Innerhalb der Spannungsquelle wirkt die Spannung vom Plus- zum Minuspol.
Die Masche M1 zeigt vom Plus- zum Minuspol, damit stehen die Richtungen der
Spannungspfeile für UR1 und UR2 fest.
Da R3 parallel zu R2 geschaltet ist, fließt der Strom in gleicher Richtung wie am Widerstand
R2. Die Richtung des Zählpfeils M2 wird beliebig festgelegt, da beide Richtungen richtig
wären.
Zur Berechnung des Stromes I berechnen wir den Gesamtwiderstand der Schaltung
R * R3
20Ω * 40Ω
800Ω 2
Rges =R1 + 2
= 20 +
= 20Ω +
= 20Ω + 13,3Ω = 33,3Ω
R2 + R3
20Ω + 40Ω
60Ω
U = R*I → I =
I =
Uq
=
Rges
U
R
2V
= 0,06 A= 60mA
33,3Ω
Der Strom I fließt am Widerstand R1
U R1 = R1 * I= 20Ω * 0,06 A= 1,2V
Innerhalb einer Masche ist die Summe der Spannungsabfälle 0 (Maschenregel)
0 = −U q1 + U R1 + U R2
U R2 =U q1 −U R1 = 2V − 1,2V = 0,8V
Der Strom I1 kann nun berechnet werden.
U R2 = R2 * I1
I1 =
U R2
0,8V
=
= 0,04 A= 40mA
R2
20Ω
Innerhalb eines Knotens sind die ankommenden und ausgehenden Ströme gleich groß
(Knotenpunktregel)
I= I1 + I 2
I2 = I − I1 = 60mA − 40mA = 20mA
Es gibt in der Regel sehr viel mehr Möglichkeiten diese Aufgaben zu berechnen die alle
gleich gut sind, z.B. hätte man im letzten Schritt nicht die Knotenpunktregel anwenden
müssen. Um I2 zu berechnen hätte man auch diesen Weg gehen können:
UR2=UR3 = 0,8V
I2=
UR3 0,8V
=
= 0,02 A = 20mA
R3
40Ω
Aufgabe 4
In diesem Gleichspannungsnetzwerk sollen die Pfeilrichtungen aller Spannungsabfälle und
Ströme (auch die Maschenrichtungen) eingetragen und anschließend berechnet werden.
Hinweis
Es gelten die gleichen Regeln wie aus der 3. Aufgabe. Dieses Netzwerk ist nur ein wenig
komplizierter. Es kann zum Verständnis helfen, wenn man sich das Netzwerk anders aufmalt,
mit der Spannungsquelle links und allen Widerständen parallel rechts. Zum Beispiel:
Lösung
Alle Pfeilrichtungen werden analog Aufgabe 3 eingezeichnet.
Um den Strom I berechnen zu können ermitteln wir den Gesamtwiderstand. Allerdings nützt
uns der Strom I im Moment noch nichts, denn er startet nicht den üblichen ‚Dominoeffekt’, da
der er an keinem der Widerstände fließt.
R23 =R2 + R3 = 50Ω + 75Ω = 125Ω
R123 =
R56 =
R1 * R23
250000Ω 2
= 117,6Ω
=
R1 + R23
2125Ω
R5 * R6
700000Ω 2
=
= 411,8Ω
R5 + R6
1700Ω
R456 = R4 + R56 = 420Ω + 411,8Ω = 831,8Ω
Rges =
R123 * R456
117,6Ω * 831,8Ω
=
= 103Ω
R123 + R456
117,6Ω + 831,8Ω
U q = Rges * I ⇒ I =
Uq
Rges
=
2,4V
= 0,0233 A = 23,3mA
103Ω
Wir können allerdings den Strom am Widerstand R1 bestimmen. R1 ist parallel zu allen
anderen Widerständen und wir wissen, dass die komplette Quellspannung an ihm wirkt.
U R1 = R1 * I5 ⇒ I5 =
U R1
2,4V
=
= 0,0012 A = 1,2mA
R1
2kΩ
Um die Ströme und Spannungen an den Widerständen R2 und R3 zu berechnen betrachten wir
die Masche M3. Wir wissen, dass an R2 und R3 der gleiche Strom I6 fließt, dass machen wir
uns zu nutze.
0 =− U q + U R2 + U R3 ⇒ U q = U R2 + U R3
U R2 = I6 * R2
U R3 = I 6 * R3
U q = I 6 * R2 + I 6 * R3 = I 6 * (R2 + R3 ) ⇒ I 6 =
Uq
R2 + R3
=
2,4V
= 0,0192 = 19,2mA
125Ω
Wir berechnen UR2 mit dem Ohmschen Gesetzt und UR3 mit der Maschenregel für M3:
U R2 = R2 * I 6 = 50Ω * 0,0192 = 0,96V
U R3 =U q − U R2 = 2,4V − 0,96V = 1,44V
Nun kennen wir auch I4 dank der Kirchhoffschen Knotenregel:
0 = I 4 − I5 − I 6 ⇒ I 4 = I5 + I 6 = 1,2mA + 19,2mA = 20,4mA
Genauso gilt:
I = I1 + I 4 ⇒ I1 = I − I 4 = 23,3mA − 20,4mA = 2,9mA
Mit I1 können wir Uq4 berechnen:
U R 4 = R4 * I1 = 420Ω * 0,0029 A = 1,218V
Wir wissen, dass an R5 und R6 die gleiche Spannung wirkt. Wir berechnen sie mit Hilfe der
Maschenregel für M1:
U q = U R 4 + U R5 ⇒ U R5 = U q − U R 4 = 2,4V − 1,218V = 1,182V
Mit UR5 = UR6 berechnen wir die beiden fehlenden Ströme:
UR5 1,182V
=
= 0,0017 A = 1,7mA
R5
700Ω
UR6 1,182V
I3 =
=
= 0,0012 A = 1,2mA
R6
1000Ω
I2 =
Den Strom I3 hätten wir beispielsweise auch mit der Knotenregel berechnen können:
I3 = I1 − I 2 = 2,9mA − 1,7mA = 1,2mA