Arbeitspunkt einer Diode

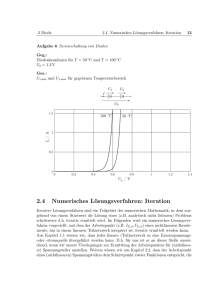
Walther-Rathenau Gewerbeschule Freiburg - Diode
Arbeitspunkt einer Diode
Uo
Liegt eine Diode mit einem Widerstand R in Reihe an
einer Spannung U0, so müssen sich die beiden diese
Spannung teilen. Vom Widerstand wissen wir, dass er
bei einer Spannung von UR einen Strom von IR =UR/R
treiben will. Das Verhältnis von Strom und Spannung an
der Diode können wir an der Kennlinie der Diode
ablesen. Da Diode und Widerstand in Reihe liegen, muss
der Strom durch beide gleich sein : IR = IF.
Es bleibt also nur die Frage, wie die beiden die
Spannung unter sich aufteilen. Um dies heraus zu
finden gibt es zwei Möglichkeiten.
Grafische Lösung
Wir wissen, dass die Spannung die nicht an der Diode abfällt für den Widerstand übrig
bleibt: UR = U0 - UF . Außerdem wissen wir über den Strom in der Diode
IF = IR = UR / R. Wenn man das ineinander einsetzt wird daraus:
IF = (U0 - UF)/ R. Was bringt das nun? Na ja, die Kennlinie der Diode gibt uns alle
„zulässigen“ Kombinationen von UF und IF aus Sicht der Diode. Die Gleichung oben gibt
uns alle „zulässigen“ Kombinationen von UF und IF aus Sicht des Widerstands.
Wenn wir die Kennlinie zu dieser Gleichung in die Diodenkennlinie einzeichnen, gibt es
einen Schnittpunkt. Dies ist dann der Arbeitspunkt auf den sich Widerstand und Diode
quasi „einigen“.
Die Gleichung IF = (U0 - UF)/ R beschreibt eine Gerade, deshalb spricht man auch von der
Arbeitsgerade des Widerstands. Diese Gerade
• schneidet die Y-Achse beim Strom IF = U0 / R
• schneidet die X-Achse bei der Spannung U
Beispiel für
U0 = 1,6 V
R=4Ω
1,6 V / 4 Ω = 400 mA
UF,AP = 1,15 V
IF,AP = IR,AP = 120 mA
UR,AP = 0,45 V
Name:
Datum:
Walther-Rathenau Gewerbeschule Freiburg - Diode
Rechnerische Lösung (Näherung)
Normalerweise vereinfachen wir die Funktion Diode derart, dass wir annehmen, sie
funktioniere wie ein Ventil mit einer konkreten Sperrspannung UF,th. Ist die äußere
Spannung größer als diese Spannung, so tun wir so, als würde über die Diode genau diese
Spannung abfallen. Der Rest bleibt für den Widerstand. Der Strom bestimmt sich dann nur
durch den Vorwiderstand:
I = (U0 – UF,th) / R
Beispiel: Für die Diode oben (Kennlinie 3) würde man eine Durchlassspannung von ca
UF,th= 0,85 annehmen (die Durchlassspannung entnimmt man in der Regel dem
Datenblatt).
Bei U0=1,6 V und
R = 4 Ω macht das einen Strom von
I = (1,6 V – 0,85 V) / 4 Ω = 187 mA
Liegt etwas neben dem Ergebnis von vorher, oder? Deshalb ist es ja auch eine Näherung.
Die Abweichung ist in diesem Beispiel recht groß, weil die Spannung U0 nicht viel größer
ist als die Durchlassspannung. Wird dieser Unterschied größer (z.B. bei U0 = 5 V), dann ist
die Abweichung tatsächlich nicht mehr nennenswert.
Vorwiderstand dimensionieren
Manchmal müssen auch Sie den Vorwiderstand dimensionieren, z.B. wenn Sie irgendwo
eine Leuchtdiode einbauen wollen. In diesem Fall arbeitet man eher mit der Näherung,
den in der Regel enthalten die Datenblätter von LEDs keine Kennlinien. Dafür findet man
die Durchlassspannung und den maximalen Strom. Letzteren sollte man nicht
überschreiten. Also setzen wir die beiden Werte mal in die Näherungsformel von vorhin
ein:
Imax = (U0 – UF,th) / R. Aber eigentlich wollen wir ja einen Widerstandswert bestimmen, also
wird die Formel umgestellt:
R = (U0 – UF,th) / Imax
Beispiel: Ein 1W Weißlichtdiode mit UF,th = 4,5 V und Imax = 350 mA braucht bei einem
Betrieb mit 12 V einen Vorwiderstand von
R = (12 V – 4,5 V) / 350 mA = 21,4 Ω.
Verlustleistung
Wenn die Diode durchgeschaltet ist, fällt natürlich auch eine Verlustleistung in der Diode
ab. Wenig überraschend berechnet sich diese so wie immer, nämlich als Produkt aus
Strom und Spannung:
PV = UF ·IF. Im LED Beispiel oben sind das also 4,5 V · 350 mA = 1,575 W. Merken Sie was?
Richtig, das sollte eigentlich eine 1 W Diode sein, da sind 1,575 W wohl doch etwas viel.
Der angegebene maximale Strom sagt nämlich erstmal nur aus, wieviel Strom die Diode
kurzzeitig verpackt. Gleichzeitig muss man aber auch die maximal zulässige
Verlustleistung der Diode beachten ! In diesem Beispiel kann man also nicht mit dem
maximalen Strom arbeiten, sondern muss den Arbeitsstrom aus der maximalen
Verlustleistung bestimmen:
Imax = Ptot /
Name:
UF,th = 222 mA
R = (12 V – 4,5 V) / 222 mA = 33,8 Ω
Datum:
Walther-Rathenau Gewerbeschule Freiburg - Diode
Übungsaufgaben
1. Bestimmen Sie für die Diode BAV 19 (Kennlinie (2) auf der ersten Seite) die
Arbeitspunkte für folgende Beschaltungen. Wenden Sie sowohl das grafische als
auch das Näherungsverfahren (mit
UF,th=850 mV) an. Bestimmen Sie auch jeweils die Verlustleistung, die an der Diode
anfällt.
a) U0 = 1,5 V
RV =
b) U0 = 2 V RV =
5
10 
2. Dimensionieren Sie den Vorwiderstand für eine rote LED (UF = 1,4V, Imax=30 mA) für
den Betrieb an einer Spannung von 5 V.
3. Dimensionieren Sie den Vorwiderstand für eine blaue LED (UF = 1,9V, Imax=25 mA,
Ptot=200 mW) für den Betrieb an einer Spannung von 5 V. Beachten Sie dabei die
maximal zulässige Verlustleistung.
4. Auch in Sperrrichtung lassen Dioden noch einen Strom durch. Vergleichen Sie die
maximalen Rückwärtsströme der BAV 99 und der BAV 18 bei einer Temperatur von
80 °C. Welche Diode sperrt schlechter?
5. Eine Diode BAV 99 soll an 12 V so betrieben werden, dass ein Strom von ca 100 mA
fliesst. Der Strom soll dabei aber auch nicht größer als 100 mA werden.
a) Nehmen Sie an, sie hätten vom Datenblatt nur die Tabelle „DC
Characteristics“ . Welche Durchlassspannung verwenden Sie für die Berechnung
des Vorwiderstands ?
b) Dimensionieren Sie den Vorwiderstand.
c) Es wird etwas wärmer (110°C) und außerdem haben Sie die Seite 4 des
Datenblatts wiedergefunden. Wie ist bei dieser Temperatur die
Durchlassspannung (Forward Voltage) der Diode ?
Bestimmen Sie den Strom, der bei dieser Temperatur durch Diode und den
Vorwiderstand aus b) fliesst.
d) Die erste Kennlinie auf Seite 3 gibt an, wie sich der maximal zulässige Strom
mit der Temperatur entwickelt. Bleibt die Diode für den in c) berechneten Fall
funktionsfähig ?
Name:
Datum:
Walther-Rathenau Gewerbeschule Freiburg - Diode
Absoluter und differentieller Widerstand
Wenn eine Diode durchgeschaltet ist, fällt über sie eine bestimmte Spannung UF ab und es
fließt ein Strom IF. Also können wir für diesen Arbeitspunkt sagen, die Diode habe den
Widerstand
R=
UF
IF
. Dabei handelt es sich um einen absoluten Widerstand, da wir mit
den Absolutwerten von Strom und Spannung rechnen. Der absolute Widerstand sagt uns,
wie gut die Diode leitet, wenn sie leitet.
Manchmal verwendet man Dioden (und andere nicht lineare Bauelemente) aber auch in
der Form, das man sie mit einer Mischspannung betreibt. Eine Mischsspannung ist
(vereinfacht gesagt) eine Überlagerung von einer Gleichspannung mit einer (oder mehrer)
Wechselspannungen. Typisch für diese Anwendung ist, das der Gleichspannungsanteil so
groß ist, dass die Diode durchgeschaltet wird. Gleichzeitig ist Amplitude der
Wechselspannung(en) verhältnismäßig klein, so das sie keinen Einfluss darauf haben, ob
die Diode durchgeschaltet bleibt oder nicht. Man könnte sagen, dass die Diode durch das
anlegen der Gleichspannung für die Wechselspannung „aufgemacht“ wird. Jetzt stellt sich
die entscheidende Frage: was ist die Diode aus Sicht der Wechselspannung ? Die Antowrt
ist: auch ein Widerstand! Allerdings wird dieser Widerstand etwas anders bestimmt, als
der absolute Widerstand.
Differentieller Widerstand
Der differentielle Widerstand
r=
U F
ist eine Näherung für den
IF
Wechselstromwiderstand eines nicht lineares Bauelement, das in einem bestimmten
Arbeitspunkt betrieben wird. Voraussetzung für die Richtigkeit der Näherung ist, das die
Amplitude (Scheitelspannung, Spitzenspannung) des angelegten Wechselstroms
ausreichend klein ist.
Für die Bestimmung des differentiellen Widerstandswerts legt man im Arbeitspunkt eine
Tangente1 an die Kennlinie. An dieser Tangente zeichnet man ein Steigungsdreick ein, und
misst die Längen der Kanten. Dadurch erhält man ein Wertepaar  U F und  I F .
Damit kann man den differentiellen Widerstand ausrechnen (Formel siehe oben).
Bestimmen Sie für die Diode BAV 19 (Kennlinie (2)) die absoluten und differentiellen
Widerstände für folgende Arbeitspunkte.
a) UF = 0,8 V
b) IF = 400 mA
1 Eine Tangente ist eine Gerade, die eine Kurve in einem Punkt berührt. Diese Gerade
hat die gleiche Steigung wie die Kurve in diesem Punkt.
Name:
Datum:
Walther-Rathenau Gewerbeschule Freiburg - Diode
Name:
Datum: