Roy, Shepard, Marshall, Hicks und Slutsky Dualität von
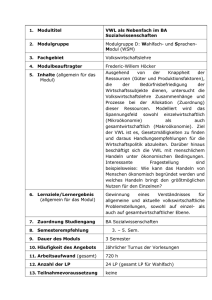
Werbung

Roy, Shepard, Marshall, Hicks und Slutsky
Dualität von Ausgabenminimierung und Nutzenmaximierung
04.07.2007 VWL III Übung 12
Tobias E. Lampe
1
Anwendung in der Konsumententheorie
Indirekte Nutzenfunktion
Indirekte
Nutzenfunktion und
Ausgabefunktion sind
Optimalwertfunktion …
Deren Lagrangian
genutzt werden
kann..
… um über das
Envelope Theorem
mit NB die parziellen
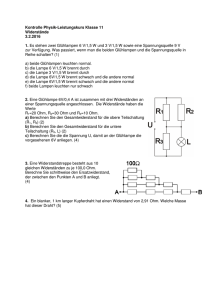
Ableitungen zu
ermitteln
Zielfunktion Nutzen, NB Budget
Ausgabefunktion:
Zielfunktion Budget, NB Nutzen
v( p, m) = max{u ( x) px = m}
e( p, u ) = min{px u ( x) = u }
L = u ( x ) − λ ( px − m)
L = px − λ (u ( x ) − u )
x
∂v
=λ
∂m
∂v
= −λx
∂p
x
∂e
= x( p, e( p, u ))
∂p
mit herzlichem Dankeschön an Herrn Dipl.-Volksw.Tobias E. Lampe
04.07.2007 VWL III Übung 12
Tobias E. Lampe
2
Roy und Shepard, Marshall und Hicks
Roys Identität und Shepards Lemma lassen sich gut als Hilfssätze einsetzen, um die
Marshallsche Nachfragefunktion bzw. die Hickssche Nachfragefunktion herzuleiten:
Nutzenmaximierung
Die indirekte Nachfragefunktion
v( p, m) = max{u ( x) px = m}
x
Ausgabenminimierung
Die Ausgabenfunktion
e( p, u ) = min{px u ( x) = u }
x
Roys Identität
Shepards Lemma
Marshallsche Nachfragefunktion
Hickssche Nachfragefunktion
∂v ∂m
x=−
∂p ∂v
x = x ( p , m)
04.07.2007 VWL III Übung 12
∂e
= x( p, e( p, u ))
∂p
h = h( p, u )
Tobias E. Lampe
3
Dualität – bei gleichen Rahmenbedingungen sind
Hickssche und Marshallsche Nachfragen identisch
(1)Das Güterbündel x* stifte bei gegebenem Einkommen m und Preisen p den optimalen Nutzen u*
(2) Dann minimiert x* gleichzeitig die Ausgaben, um bei gegebenen Preisen p das Nutzenniveau u*
zu erreichen!
(1) Bei gegebener Budgetgerade
kann kein höheres Nutzenniveau
v
als v erlangt werden
(2) Bei gegebenem Nutzenniveau
kann keine „tiefere“ Budgetgerade
als e erreicht werden
Damit folgt im Optimum:
h( p, u ) ≡ x ( p, m( p, u ))
Æ
∂h ∂x
∂xi
= i − i xj
∂p j ∂p j ∂m
Slutsky
Gleichung
(über parzielles Differenzieren beider Seiten Beweis siehe Vorlesungsprotokoll)
e
04.07.2007 VWL III Übung 12
Tobias E. Lampe
4
Die Preiseffekte auf Hickssche und Marshallsche
Nachfragen sind jedoch unterschiedlich
Marshall
x1
Der Preis von Gut 2 fällt…
x2
p2
04.07.2007 VWL III Übung 12
Tobias E. Lampe
5
Die Preiseffekte auf Hickssche und Marshallsche
Nachfragen sind jedoch unterschiedlich
Marshall
x1
Der Preis von Gut 2 fällt…
Die Budgetgerade rotiert nach
außen…
x2
p2
04.07.2007 VWL III Übung 12
Tobias E. Lampe
6
Die Preiseffekte auf Hickssche und Marshallsche
Nachfragen sind jedoch unterschiedlich
Marshall
x1
Der Preis von Gut 2 fällt…
Die Budgetgerade rotiert nach
außen…
Der Konsument erreicht ein
höheres Nutzenniveau…
x2
p2
Die nachgefragten Menge steigt
04.07.2007 VWL III Übung 12
Tobias E. Lampe
7
Die Preiseffekte auf Hickssche und Marshallsche
Nachfragen sind jedoch unterschiedlich
Marshall
x1
Hicks
x1
Der Preis von Gut 2 fällt…
Der Preis von Gut 2 fällt…
Die Budgetgerade rotiert nach
außen…
Die Budgetgerade rotiert nach
außen…
Der Konsument erreicht ein
höheres Nutzenniveau…
x2
x2
p2
p2
Die nachgefragten Mengen steigt
(aber nicht so stark wie links,
denn das Einkommen ist reduziert
worden!)
Die nachgefragten Menge steigt
04.07.2007 VWL III Übung 12
Tobias E. Lampe
8
Die Preiseffekte auf Hickssche und Marshallsche
Nachfragen sind jedoch unterschiedlich
Marshall
x1
Hicks
x1
Der Preis von Gut 2 fällt…
Die Budgetgerade rotiert nach
außen…
Die Budgetgerade rotiert nach
außen…
Der Konsument erreicht ein
höheres Nutzenniveau…
Der Konsument kann seine
Ausgaben reduzieren
x2
x2
p2
p2
Der Preis von Gut 2 fällt…
Die nachgefragte Mengen steigt
(aber nicht so stark wie links,
denn das Einkommen ist reduziert
worden!)
Die nachgefragten Menge steigt
x2
04.07.2007 VWL III Übung 12
x2
Tobias E. Lampe
9
Slutsky Gleichung: Hicksche Nachfrageanpassung als
Komponente der Marshallschen Nachfrageanpasung
∂h ∂x
∂xi
= i − i xj
∂p j ∂p j ∂m
x1
Slutsky Gleichung
∂ xi ∂ hi ∂ xi
=
−
xi
∂pi ∂pi ∂m
Slutsky Zerlegung für
eine Veränderung
des eigenen Preises
∂xi
∂h
∂x
Δpi = i Δpi − i xi Δpi
∂pi
∂pi
∂m
Mengeneffekt bei diskreter
Preisänderung
Gesamteffekt
x2
04.07.2007 VWL III Übung 12
Tobias E. Lampe
10
Slutsky Gleichung: Hicksche Nachfrageanpassung als
Komponente der Marshallschen Nachfrageanpasung
∂h ∂x
∂xi
= i − i xj
∂p j ∂p j ∂m
x1
Hicksscher
Substitutionseffekt1
Slutsky Gleichung
∂ xi ∂ hi ∂ xi
=
−
xi
∂pi ∂pi ∂m
Slutsky Zerlegung für
eine Veränderung
des eigenen Preises
∂xi
∂h
∂x
Δpi = i Δpi − i xi Δpi
∂pi
∂pi
∂m
Mengeneffekt bei diskreter
Preisänderung
Einkommenseffekt
Gesamteffekt
x2
1 Es gibt unterschiedliche Definitionen des Substitutionseffektes. An der Stelle tragen unterschiedliche Quellen zur Verwirrung bei – lassen Sie uns für diesen Kurs obige Definition als Standard festlegen
04.07.2007 VWL III Übung 12
Tobias E. Lampe
11
Slutsky Gleichung: Hicksche Nachfrageanpassung als
Komponente der Marshallschen Nachfrageanpasung
x1
Hicksscher
Substitutionseffekt1
Einkommenseffekt
x2
p2
Marshallsche Nachfragekurve
H1
x2
1 Es gibt unterschiedliche Definitionen des Substitutionseffektes. An der Stelle tragen unterschiedliche Quellen zur Verwirrung bei – lassen Sie uns für diesen Kurs obige Definition als Standard festlegen
04.07.2007 VWL III Übung 12
Tobias E. Lampe
12







![Aufgabe 10 Produktivität [5 Punkte]](http://s1.studylibde.com/store/data/002218019_1-b24954608f2bcfd061d06ba5fecb3a31-300x300.png)

![Aufgabe 7 Produktivität [5 Punkte]](http://s1.studylibde.com/store/data/002054622_1-3a545f02a634c0b2b66d1a220be3e293-300x300.png)