pythagoräische Tripel pythagorean triplets - Sinus-SH

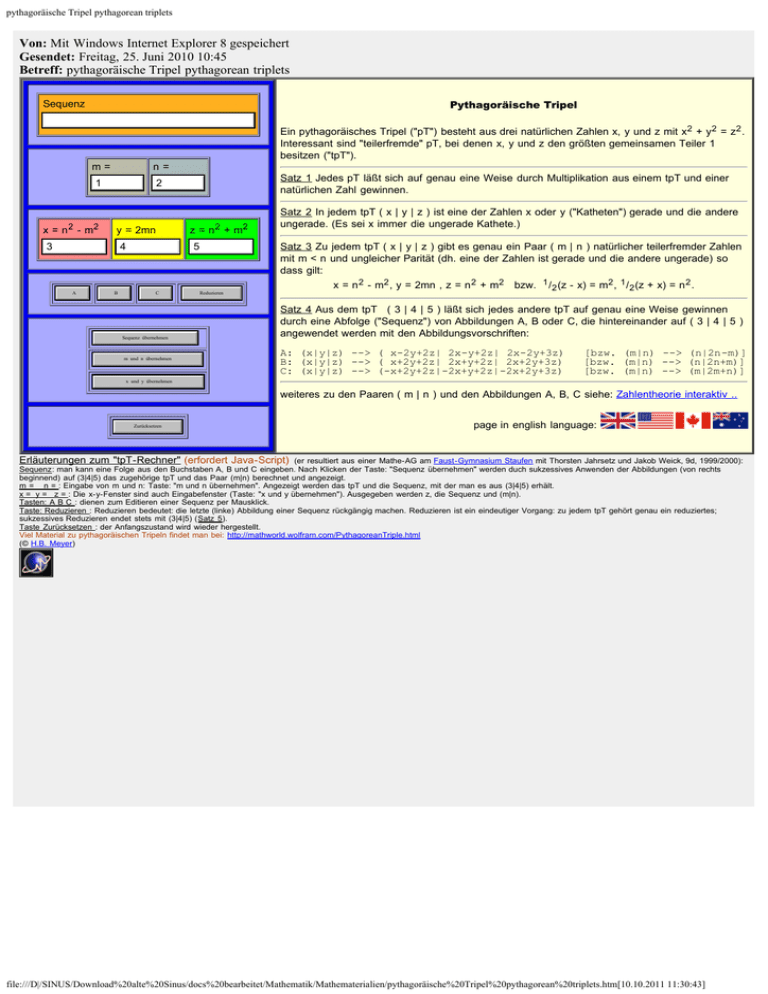
pythagoräische Tripel pythagorean triplets
Von: Mit Windows Internet Explorer 8 gespeichert
Gesendet: Freitag, 25. Juni 2010 10:45
Betreff: pythagoräische Tripel pythagorean triplets
Pythagoräische Tripel
Sequenz
Ein pythagoräisches Tripel ("pT") besteht aus drei natürlichen Zahlen x, y und z mit x 2 + y 2 = z 2 .
Interessant sind "teilerfremde" pT, bei denen x, y und z den größten gemeinsamen Teiler 1
besitzen ("tpT").
m =
n =
1
2
x = n 2 - m2
y = 2mn 3
4
A
B
Satz 1 Jedes pT läßt sich auf genau eine Weise durch Multiplikation aus einem tpT und einer
natürlichen Zahl gewinnen.
z = n 2 + m2
Satz 3 Zu jedem tpT ( x | y | z ) gibt es genau ein Paar ( m | n ) natürlicher teilerfremder Zahlen
mit m < n und ungleicher Parität (dh. eine der Zahlen ist gerade und die andere ungerade) so
dass gilt:
5
C
Sequenz übernehmen
m und n übernehmen
Satz 2 In jedem tpT ( x | y | z ) ist eine der Zahlen x oder y ("Katheten") gerade und die andere
ungerade. (Es sei x immer die ungerade Kathete.)
Reduzieren
x = n 2 - m2 , y = 2mn , z = n 2 + m2 bzw. 1 /2 (z - x) = m2 , 1 /2 (z + x) = n 2 .
Satz 4 Aus dem tpT ( 3 | 4 | 5 ) läßt sich jedes andere tpT auf genau eine Weise gewinnen
durch eine Abfolge ("Sequenz") von Abbildungen A, B oder C, die hintereinander auf ( 3 | 4 | 5 )
angewendet werden mit den Abbildungsvorschriften:
A: (x|y|z) --> ( x-2y+2z| 2x-y+2z| 2x-2y+3z) [bzw. (m|n) --> (n|2n-m)]
B: (x|y|z) --> ( x+2y+2z| 2x+y+2z| 2x+2y+3z) [bzw. (m|n) --> (n|2n+m)]
C: (x|y|z) --> (-x+2y+2z|-2x+y+2z|-2x+2y+3z) [bzw. (m|n) --> (m|2m+n)]
x und y übernehmen
weiteres zu den Paaren ( m | n ) und den Abbildungen A, B, C siehe: Zahlentheorie interaktiv ..
Zurücksetzen
page in english language:
Erläuterungen zum "tpT-Rechner" (erfordert Java-Script) (er resultiert aus einer Mathe-AG am Faust-Gymnasium Staufen mit Thorsten Jahrsetz und Jakob Weick, 9d, 1999/2000):
Sequenz: man kann eine Folge aus den Buchstaben A, B und C eingeben. Nach Klicken der Taste: "Sequenz übernehmen" werden duch sukzessives Anwenden der Abbildungen (von rechts
beginnend) auf (3|4|5) das zugehörige tpT und das Paar (m|n) berechnet und angezeigt.
m = n = : Eingabe von m und n: Taste: "m und n übernehmen". Angezeigt werden das tpT und die Sequenz, mit der man es aus (3|4|5) erhält.
x = y = z = : Die x-y-Fenster sind auch Eingabefenster (Taste: "x und y übernehmen"). Ausgegeben werden z, die Sequenz und (m|n).
Tasten: A B C : dienen zum Editieren einer Sequenz per Mausklick.
Taste: Reduzieren : Reduzieren bedeutet: die letzte (linke) Abbildung einer Sequenz rückgängig machen. Reduzieren ist ein eindeutiger Vorgang: zu jedem tpT gehört genau ein reduziertes;
sukzessives Reduzieren endet stets mit (3|4|5) (Satz 5).
Taste Zurücksetzen : der Anfangszustand wird wieder hergestellt.
Viel Material zu pythagoräischen Tripeln findet man bei: http://mathworld.wolfram.com/PythagoreanTriple.html
(© H.B. Meyer)
file:///D|/SINUS/Download%20alte%20Sinus/docs%20bearbeitet/Mathematik/Mathematerialien/pythagoräische%20Tripel%20pythagorean%20triplets.htm[10.10.2011 11:30:43]